Projekt „Flächeninhalt- und Umfangsberechnung
Werbung

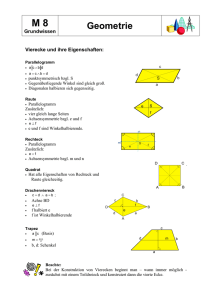
Projekt „Flächeninhalt- und Umfangsberechnung“ für die 7. Schulstufe einer KMS Beginn mit einer Einführungsstunde im Frontalunterricht: Wiederholung von Flächeninhalt und Umfang beim Rechteck und Quadrat (zählen von Quadratkästchen in einer Reihe mal Anzahl der Reihen bis zur Flächeninhaltsformel). Problembewusstsein schaffen beim Abzählen von nicht rechtwinkeligen Flächen (Dreieck, Parallelogramm, etc). Arbeitsplan erklären! Siehe Arbeitsplan auf Seite 23 und 24. Konzipiert als Stationenbetrieb oder für „ individuelles Lernen“. im Stationenbetrieb: auf mehrere Räume aufgeteilt (Raumschilder) als individuelle Lernphase im Klassenverband (Aufgabenzettel und Legematerial von einem Materialtisch zu holen) Wir haben das Projekt im Stationenbetrieb durchgeführt. In jedem „Flächenraum“ (ein mit einem bestimmten Raumschild gekennzeichneter Arbeitsraum) wurde ein großes Plakat mit der zu bearbeiteten Fläche (eingezeichnet alle für die Berechnung notwendigen Strecken und vollständig beschriftet) aufgehängt. Da das Thema sehr aufbauend ist, mussten die SchülerInnen zuerst die roten, dann die grünen und zum Schluss die blau markierten Beispiele lösen. Die Beispieltische waren mit den entsprechenden Farben markiert. (Es war aber egal zuerst einen Raum vollständig fertig zu machen, z. B. den Trapezraum, oder zuerst alle roten Beispiele, dann alle grünen usw. zu erledigen.) Inhalt: Zum verwendeten Unterrichtsbuch ………………………………………………………………………………….………… 2 Raumschilder …………………………………………………………………………………………………………………….………… 3 rote Aufgaben (Aufgaben zum Verständnis der zu bearbeitenden Flächen) …………………….………… 6 Legespiele ……………………………………………………………………………………………………………………….………… 6 Zeichenaufgaben (mit Hilfe des Koordinatensystems, 1. Quadrant) ……………………………………… 10 Flächenteile zum Ausschneiden für das Legespiel …………………………………………………………………… 12 grüne Aufgaben (Rechenbeispiele verschiedenster Schwierigkeitsstufen) ………………………………… 16 Domino (Formeltrainer) …………………………………………………………………………………………………………… 20 Zuordnungsaufgaben (Nagelbrett als Formeltrainer) ……………………………………………………………… 21 Arbeitsplan (Doppelseitig in Klassenstärke kopieren, von SchülerInnen die Smilies nach Vorlage anmalen lassen) ………………………………………………………………………………………………………………….………… 23 blaue Aufgaben (Arbeitsaufträge zur Erarbeitung der Flächeninhalts- und Umfangsformeln) ..… 25 erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 1 Wir haben das in den Klassen verwendete Schulbuch in die Arbeit einbezogen: Ingrid Lewisch; Mathematik Verstehen – Üben – Anwenden; Band 3, 4. Auflage, Wien 2002. Überall dort, wo Bezug auf ein Rechenbeispiel genommen wird, fehlt die Angabe der Buchseite und Beispielnummer, um auch jenen die Projektunterlagen anbieten zu können, die nicht unser Buch im Unterricht verwenden. Für oben erwähntes Buch folgt hier jeder Arbeitsauftrag mit Seitenangaben und Aufgabennummer (die einzusetzten sind). Zusammenfassung der im „Projekt“ zu erledigenden Buchaufgaben: Rechenbeispiele Parallelogramm! Seite 91: 496, 497 Rechenbeispiele Trapez! Seite 95: 520, 521 Rechenbeispiele Deltoid! Seite 99: 541 Rechenbeispiele Raute (Rhombus)! Seite 94: 513 Noch mehr Flächenberechnungen! Rechenbeispiele Dreiecke! Umkehraufgaben Dreiecke! Seite 88: 477 Seite 90: 491 Seite 90: 489, 490, 492, 493 Seite 88: 478 Noch mehr Umkehraufgaben zum Dreieck! Umkehraufgaben Parallelogramm! Umkehraufgaben Trapez! Seite 99: 540 Seite 98: 537 Seite 101 alle Seite 87: 471, 472 Noch mehr Rechenbeispiele Dreiecke! Seite 92: 499 Seite 88: 480, 483 Seite 93: 509,510 Seite 97: 530, 531 Noch mehr Umkehraufgaben Parallelogramm! Umkehraufgaben Deltoid (Drache)! Seite 93: 512 Seite 100: 544 Umkehraufgaben Raute, Deltoid und Quadrat! Seite 100: 543, 546 erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 2 Raumschilder DreieckRaum ParallelogrammRaum erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 3 Trapez-Raum Deltoid (Drachen)-Raum erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 4 weitere FlächenRaum erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 5 rote Beispiele (nur wenige Kopien notwendig) Legespiel allgemeines Dreieck Lege die gegebene Fläche mit den vorgegebenen Flächenteilen vollständig aus. Kannst du die dazu benötigten Teile so zusammenlegen, dass ein Rechteck entsteht? Wenn das nicht gelingt, versuche es mit der doppelten Anzahl von Flächenteilen. Legespiel rechtwinkeliges Dreieck Lege die gegebene Fläche mit den vorgegebenen Flächenteilen vollständig aus. Kannst du die dazu benötigten Teile so zusammenlegen, dass ein Rechteck entsteht? Wenn das nicht gelingt, versuche es mit der doppelten Anzahl von Flächenteilen. erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 6 Legespiel Parallelogramm Lege die gegebene Fläche mit den vorgegebenen Flächenteilen vollständig aus. Kannst du die dazu benötigten Teile so zusammenlegen, dass ein Rechteck entsteht? Legespiel Trapez Lege die gegebene Fläche mit den vorgegebenen Flächenteilen vollständig aus. Kannst du die dazu benötigten Teile so zusammenlegen, dass ein Rechteck entsteht? Wenn das nicht gelingt, versuche es mit der doppelten Anzahl von Flächenteilen. erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 7 Legespiel Deltoid (Drachen) Lege die gegebene Fläche mit den vorgegebenen Flächenteilen vollständig aus. Kannst du die dazu benötigten Teile so zusammenlegen, dass ein Rechteck entsteht? erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 8 Legespiel Raute (Rhombus) Lege die gegebene Fläche mit den vorgegebenen Flächenteilen vollständig aus. Kannst du die dazu benötigten Teile so zusammenlegen, dass ein Rechteck entsteht? erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 9 Zeichne das allgemeine Dreieck! Arbeite im Heft: Schreibe die Überschrift ALLGEMEINES DREIECK. Zeichne das Dreieck indem du im Koordinatensystem die Eckpunkte A (2/2), B (11/4) und C (8/6) miteinander verbindest. Zeichne die Höhe hc, hb und ha ein. Immer im rechten Winkel zur Seite! Welche Seiten stehen parallel zueinander? ___________ Welche Strecken stehen im rechten Winkel aufeinander? __________ Zeichne das rechtwinkelige Dreieck! Arbeite im Heft: Schreibe die Überschrift RECHTWINKELIGES DREIECK. Zeichne das Dreieck indem du im Koordinatensystem die Eckpunkte A (1/2), B (11/2) und C (9/6) miteinander verbindest. Zeichne die Höhe hc ein. Immer im rechten Winkel zur Seite c! Welche Seiten stehen parallel zueinander? ___________ Welche Strecken stehen im rechten Winkel aufeinander? __________ Zeichne das Parallelogramm! Arbeite im Heft: Schreibe die Überschrift PARALLELOGRAMM. Zeichne das Parallelogramm indem du im Koordinatensystem die Eckpunkte A (0/2), B (7/2), C (10/7) und D (3/7) miteinander verbindest. Zeichne die Höhe h ein. Welche Seiten stehen parallel zueinander? ___________ und ___________ Welche Strecken stehen im rechten Winkel aufeinander? _______und _______ Zeichne das Trapez! Arbeite im Heft: Schreibe die Überschrift TRAPEZ. Zeichne das Trapez indem du im Koordinatensystem die Eckpunkte A (2/2), B (11/2), C (7/6) und D (3/6) miteinander verbindest. Zeichne die Höhe h ein. Welche Seiten stehen parallel zueinander? ___________ Welche Strecken stehen im rechten Winkel aufeinander? __________ erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 10 Zeichne das Deltoid! Arbeite im Heft: Schreibe die Überschrift DELTOID (DRACHEN). Zeichne das Deltoid indem du im Koordinatensystem die Eckpunkte A (3/9), B (0/6), C (3/0) und D (6/6) miteinander verbindest. Zeichne die Diagonalen ein. Welche Seiten stehen parallel zueinander? _____ Welche Strecken stehen im rechten Winkel aufeinander? __________ Zeichne die Raute (Rhombus)! Arbeite im Heft: Schreibe die Überschrift Raute (RHOMBUS). Zeichne die Raute indem du im Koordinatensystem die Eckpunkte A (1/1), B (5,5/1), C (7,5/5) und D (3/5) miteinander verbindest. Zeichne die Diagonalen ein. Welche Seiten stehen parallel zueinander? ____ und ______ Welche Strecken stehen im rechten Winkel aufeinander? __________ Zeichne die Raute genauso noch einmal. Nun zeichnest du die Höhen h ein. Welche Seiten stehen parallel zueinander? _______ und ________ Welche Strecken stehen im rechten Winkel zueinander? ______ und _________ erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 11 Flächenteile zum Ausschneiden für die Legespiele Flächenteile allgemeines Dreieck (auf färbiges Papier kopiert) Flächenteile rechtwinkeliges Dreieck (auf färbiges Papier kopiert) Flächenteile Parallelogramm (auf färbiges Papier kopiert) erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 12 Flächenteile Trapez (auf färbiges Papier kopiert) erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 13 Flächenteile Raute (auf färbiges Papier kopiert) erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 14 Flächenteile Deltoid (auf färbiges Papier kopiert) erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 15 grüne Aufgaben (nur wenige Kopien notwendig) Rechenbeispiele Parallelogramm! Schreibe dir noch einmal die Flächenformeln des Parallelogramms auf (im Buch Seite ____ findest du Hilfe): A= = Nun rechnest du die folgenden Beispiele in dein Heft. Seite ____ Nr. ____, _____ Seite ____ Nr. _____. Rechenbeispiele Trapez! Schreibe dir noch einmal die Flächenformel des Trapezes auf (im Buch Seite ___ findest du Hilfe): A= Nun rechnest du die folgenden Beispiele in dein Heft. Seite ____ Nr. ____, ____. Rechenbeispiele Deltoid! Schreibe dir noch einmal die Flächenformel des Deltoids (Drachen) auf (im Buch Seite ___ findest du Hilfe): A= Nun rechnest du die folgenden Beispiele in dein Heft. Seite ____ Nr. _____ Rechenbeispiele Raute (Rhombus)! Schreibe dir noch einmal die Flächenformeln der Raute auf (im Buch Seite ____ und _____ findest du Hilfe): A= = Nun rechnest du die folgenden Beispiele in dein Heft. Seite ____ Nr. ____ Seite ____ Nr. ____ erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 16 noch mehr Flächenberechnungen! 1) Buch Seite ___ Nummer ____ (hier handelt es sich um Flächen, die aus mehreren Trapezen bestehen. 2) Wie viele der Beispiele auf Seite ____ kannst du rechnen? Alle? Versuche es! Die Lehrer werden dir gerne helfen! Rechenbeispiele Dreiecke! Löse folgende Aufgaben mit den dir bekannten Dreiecksformeln! Buch Seite ___ Nr. ____, ____, Buch Seite ___ Nr. ____ und Buch Seite ___ Nr. _____. Umkehraufgaben Dreiecke! Wenn der Flächeninhalt A und eine Seite oder eine Höhe bekannt ist, kannst du die fehlende Größe (Höhe oder Seite) ausrechnen. Dazu hilft dir das, was du bei den Gleichungen gelernt hast. Schaue dir im Buch Seite ___ das Übungsbeispiel (grüner Kasten) zu den Beispielen Nr. ____ an: A = 20 cm² c = 8 cm Du löst mit einer Gleichung: So kannst du die Beispiele von Nr. 478 lösen. Dabei ist es egal, ob einmal eine Seite oder eine Höhe fehlt. erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 17 Noch mehr Umkehraufgaben zum Dreieck! Löse die Beispiele Buch Seite ___ Nr. ____ und ____. Noch mehr Rechenbeispiele Dreiecke! Löse die Aufgaben mit den dir bekannten Dreiecksformeln! Buch Seite ___ Nr. _____, _____, _____, ____. Umkehraufgaben Parallelogramm! Wenn der Flächeninhalt A und eine Seite oder eine Höhe bekannt ist, kannst du die fehlende Größe (Höhe oder Seite) ausrechnen. Dazu hilft dir das, was du bei den Gleichungen gelernt hast. Schaue dir im Buch Seite ___ das Übungsbeispiel (grüner Kasten) zu den Beispielen Nr. ______ an: A = 120 cm² a = 15 cm Du löst mit einer Gleichung: Genauso kannst du jetzt die Beispiele Seite _____ Nr. ______ und _____ lösen. Umkehraufgaben Raute, Deltoid und Quadrat! Löse mit Hilfe der dir nun bekannten Flächenformeln folgende Aufgaben! Buch Seite _____: Nr. _____ und Nr. ______. erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 18 Umkehraufgaben Trapez! Wenn beim Trapez der Flächeninhalt A gegeben ist, aber eine der parallelen Seiten oder die Höhe fehlt, kannst du die fehlende Größe (Höhe oder Seite) ausrechnen. Dazu hilft dir das, was du bei den Gleichungen gelernt hast. Schaue dir im Buch Seite ______ das Übungsbeispiel (rotumrandeter Kasten) genau an! Du löst mit einer Gleichung! Dann kannst du die Beispiele Buch Seite ____ Nr. ______ und ______ berechnen. Noch mehr Umkehraufgaben Parallelogramm! Löse das Beispiel Buch Seite _____ Nr. _________. Umkehraufgaben Deltoid (Drache)! Wenn beim Deltoid der Flächeninhalt A und eine Diagonale gegeben ist, kannst du die andere fehlende Diagonale ausrechnen. Dazu hilft dir das, was du bei den Gleichungen gelernt hast. Zum Beispiel ist der Flächeninhalt A = 56 m² und die Diagonale BD = 7m. Du löst mit einer Gleichung! Dann kannst du die Beispiele Buch Seite ____ Nr. _____ berechnen. erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 19 Flächeninhalt Umfang rechtwinkeliges Quadrat, Raute Flächeninhalt Quadrat Flächeninhalt Raute (Rhombus) Umfang Rechteck, Deltoid, Parallelogramm Umfang Dreieck A = a² Dreieck u = a+b+c+d A=a.b Umfang Trapez Flächeninhalt Rechteck Flächeninhalt Trapez Flächeninhalt Deltoid (Drache) Flächeninhalt Flächeninhalt Parallelogramm allg. Dreieck U = 2a + 2b U=a+b+c A = a . ha = b . hb erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at U = 4a 20 Ordne zu! A Rechteck A = a . ha = b . hb A allgemeines Dreieck A Parallelogramm U = 2a + 2b A Quadrat A Deltoid (Drachen) A=a.b A Raute (Rhombus) A rechtwinkeliges Dreieck U Rechteck, Parallelogramm, Deltoid U = a+b+c+d U = 4a U Trapez A = a² U Quadrat, Raute erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 21 Ordne zu! U Quadrat, Raute U = 2a + 2b U Trapez U Rechteck, Parallelogramm, Deltoid A Quadrat A rechtwinkeliges Dreieck A allgemeines Dreieck A Trapez U = 4a A = a . ha = b . hb U = a +b +c +d A Deltoid (Drache) A Rechteck A Parallelogramm A = a² A=a.b erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 22 ARBEITSPLAN Name: ________________________________ Station Legespiel allgemeines Dreieck Legespiel rechtwinkeliges Dreieck Zeichne ein rechtwinkeliges Dreieck! Zeichne ein allgemeines Dreieck! Beschrifte ein rechtwinkeliges Dreieck richtig! Beschrifte ein allg. Dreieck richtig! Umfangberechnung Dreieck Flächeninhaltsberechnung allgemeines Dreieck! Flächeninhaltsberechnung rechtwinkeliges Dreieck! Rechenbeispiele Dreiecke! Noch mehr Rechenbeispiele Dreiecke! Umkehraufgaben Dreiecke! Noch mehr Umkehraufgaben Dreiecke! Legespiel Parallelogramm Zeichne das Parallelogramm! Beschrifte das Parallelogramm richtig! Umfangberechnung Parallelogramm! Flächeninhaltsberechnung Parallelogramm! Rechenbeispiele Parallelogramm! Umkehraufgaben Parallelogramm! Noch mehr Umkehraufgaben Parallelogramm! Legespiel Trapez Zeichne das Trapez! Beschrifte das Trapez richtig! Umfangberechnung Trapez! Flächeninhaltsberechnung Trapez! Rechenbeispiele Trapez! Umkehraufgaben Trapez! Sozialform ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ☺ ! ! ! ! ! ! ! ! ? ! ? ☺ ! ! ! ! ! ! ? ☺ ! ! ! ! ! ! Material Erledigt? ! ! Heft, Füller, Bleistift, Geodreieck Heft, Füller, Bleistift, Geodreieck Füller, Kleber Füller, Kleber Füller, Farbstift, Heft, Kleber Füller, Schere, Heft, Kleber Füller, Schere, Heft, Kleber Heft, Buch, Füller Heft, Buch, Füller Heft, Buch, Füller Heft, Buch, Füller ! Heft, Füller, Bleistift, Geodreieck Füller, Kleber Füller, Farbstift, Heft, Kleber Füller, Schere, Heft, Kleber Heft, Buch, Füller Heft, Buch, Füller Heft, Buch, Füller ! Heft, Füller, Bleistift, Geodreieck Füller, Kleber Füller, Farbstift, Heft, Kleber Füller, Schere, Heft, Kleber Heft, Buch, Füller Heft, Buch, Füller erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 23 Flächenberechnung Trapez mit Mittellinie! Legespiel Deltoid Zeichne das Deltoid! Beschrifte das Deltoid richtig! Umfangberechnung Deltoid! Flächeninhaltsberechnung Deltoid! Rechenbeispiele Deltoid! Umkehraufgaben Deltoid! Legespiel Raute Zeichne die Raute! Beschrifte die Raute richtig! Umfangberechnung Raute! Flächeninhaltsberechnung Raute! Rechenbeispiele Raute! Quadrat einmal anders! Umkehraufgaben Raute, Deltoid und Quadrat! Ordne zu! Formel-Domino noch mehr Flächenberechnungen ☺ rot zuerst, dann ☺ ☺? ☺☺! ☺! ☺! ☺! ☺! ☺! ☺! ☺☺? ☺? ☺? ☺? ☺? ☺? ☺? ☺? ☺! ☺☺! ☺? blau, zum Schluss ☺ Füller, Schere, Heft, Kleber, Buch Heft, Füller, Bleistift, Geodreieck Füller, Kleber Füller, Farbstift, Heft, Kleber Füller, Schere, Heft, Kleber Heft, Buch, Füller Heft, Buch, Füller Heft, Füller, Bleistift, Geodreieck Füller, Kleber Füller, Farbstift, Heft, Kleber Füller, Schere, Heft, Kleber Heft, Buch, Füller Füller, Schere, Heft, Kleber, Buch Heft, Buch, Füller Nagelbrett Dominospielsteine Heft, Buch, Füller grün ! …. das musst du erledigen ? …. das kannst du erledigen erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 24 blaue Arbeitsaufträge (in Klassenstärke) Beschrifte das allgemeine Dreieck richtig! Alle Buchstaben und Symbole müssen in diesem Dreieck ihren richtigen Platz finden. Strecken: a, b, c, ha, hb, hc Ecken: A, B, C Symbole: (3-mal kannst du dieses Symbol einsetzen) Klebe diesen Zettel in dein Heft. Umfangberechnung Dreieck! Beschrifte die Seiten! Ziehe die Seiten einzeln mit einem bunten Stift nach. Notiere dir dabei immer, welche Seite du gerade nachgezogen hast. Seite Seite 1. Seite 2. 3. U Umfangsformel: U = + + _ Klebe diesen Zettel in dein Heft. erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 25 Beschrifte das rechtwinkelige Dreieck richtig! Alle Buchstaben und Symbole müssen in diesem Dreieck ihren richtigen Platz finden. Strecken: a, b, c, hc Ecken: A, B, C Symbole: (2-mal kannst du dieses Symbol einsetzen) Klebe diesen Zettel in dein Heft. Flächeninhaltsberechnung allgemeines Dreieck! Beschrifte die dick markierten Linien! Schneide beide Flächen aus und zerschneide eine Fläche entlang der markierten Linien. Lege die Teile so auf, dass ein Rechteck entsteht! Wie heißt die Länge dieses Rechtecks? _____________ Wie heißt die Breite dieses Rechtecks? _____________ Wie heißt die Flächenformel dieses Rechtecks? _________________ Wie muss die Flächenformel der gefärbten Fläche lauten? __________________ Beginne beim Beschriften mit einer anderen Seite. Wie heißt dann deine Formel? Flächeninhaltsformel allgemeines Dreieck: A = = = _ Klebe die Teile, so wie du sie gelegt hast, in dein Heft. Schreibe die Formel darunter! erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 26 Beschrifte das Trapez richtig! Alle Buchstaben und Symbole müssen in diesem Trapez ihren richtigen Platz finden. Strecken: a, b, c, d, h Ecken: A, B, C, D Symbole: (2-mal kannst du dieses Symbol einsetzen) Klebe diesen Zettel in dein Heft. Flächeninhaltsberechnung rechtwinkeliges Dreieck! Beschrifte die dick markierten Linien! Schneide beide Flächen aus! Lege die Teile so auf, dass ein Rechteck entsteht! Wie heißt die Länge dieses Rechtecks? _____________ Wie heißt die Breite dieses Rechtecks? _____________ Wie heißt die Flächenformel dieses Rechtecks? _________________ Wie muss die Flächenformel der gefärbten Fläche lauten? __________________ Flächeninhaltsformel rechtwinkeliges Dreieck: A = _ Klebe die Teile, so wie du sie gelegt hast, in dein Heft. Schreibe die Formel darunter! erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 27 Umfangberechnung Trapez! Beschrifte die Seiten! Ziehe die Seiten einzeln mit einem bunten Stift nach. Notiere dir dabei immer, welche Seite du gerade nachgezogen hast. Seite Seite Seite 4. Seite 5. 6. 7. U Umfangsformel: U = + + + _ Klebe diesen Zettel in dein Heft. Flächeninhaltsberechnung Trapez! Beschrifte die dick markierten Linien! Schneide beide Flächen aus und zerschneide eine Fläche entlang der markierten Linien. Lege die Teile so auf, dass ein Rechteck entsteht! Wie heißt die Länge dieses Rechtecks? _____________ Wie heißt die Breite dieses Rechtecks? _____________ Wie heißt die Flächenformel dieses Rechtecks? _________________ Wie muss die Flächenformel der gefärbten Fläche lauten? __________________ Flächeninhaltsformel TRAPEZ: A = _ Klebe die Teile, so wie du sie gelegt hast, in dein Heft. Schreibe die Formel darunter! erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 28 Beschrifte das Parallelogramm richtig! Alle Buchstaben und Symbole müssen in diesem Parallelogramm ihren richtigen Platz finden. Strecken: a, a, b, b, ha, hb Ecken: A, B, C, D Symbole: (4-mal kannst du dieses Symbol einsetzen) Klebe diesen Zettel in dein Heft. Flächeninhaltsberechnung Parallelogramm! Beschrifte die dick markierten Linien! Schneide beide Flächen aus und zerschneide die Fläche entlang der markierten Linien. Lege die Teile so auf, dass ein Rechteck entsteht! Wie heißt die Länge dieses Rechtecks? _____________ Wie heißt die Breite dieses Rechtecks? _____________ Wie heißt die Flächenformel dieses Rechtecks? _________________ Flächeninhaltsformel PARALLELOGRAMM: A = _ Klebe die Teile, so wie du sie gelegt hast, in dein Heft. Schreibe die Formel darunter! erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 29 Umfangberechnung Parallelogramm! Beschrifte die Seiten! Ziehe die Seiten einzeln mit einem bunten Stift nach. Notiere dir dabei immer, welche Seite du gerade nachgezogen hast. Seite Seite Seite 1. Seite 2. 3. 4. U Umfangsformel: U = + + + = + _ Klebe diesen Zettel in dein Heft. Flächeninhaltsberechnung Deltoid! Beschrifte die dick markierten Linien! Schneide beide Flächen aus und zerschneide die Fläche entlang der markierten Linien. Lege die Teile so auf, dass ein Rechteck entsteht! Wie heißt die Länge dieses Rechtecks? _____________ Wie heißt die Breite dieses Rechtecks? _____________ Wie heißt die Flächenformel dieses Rechtecks? _________________ Flächeninhaltsformel DELTOID (DRACHEN): A =___________________ Klebe die Teile, so wie du sie gelegt hast, in dein Heft. Schreibe die Formel darunter! erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 30 Beschrifte das Deltoid (Drachen) richtig! Alle Buchstaben und Symbole müssen in diesem Drachen ihren richtigen Platz finden. Strecken: a, a, b, b, e, f/2, f/2, Ecken: A, B, C, D Symbole: Klebe diesen Zettel in dein Heft. Umfangberechnung Deltoid (Drachen)! Beschrifte die Seiten! Ziehe die Seiten einzeln mit einem bunten Stift nach. Notiere dir dabei immer, welche Seite du gerade nachgezogen hast. Seite Seite Seite 1. Seite 2. 3. 4. U Umfangsformel: U = + + + = + _ Klebe diesen Zettel in dein Heft. Beschrifte die Raute (Rhombus) richtig! Alle Buchstaben und Symbole müssen in diesem Drachen ihren richtigen Platz finden. Strecken: a (je 4-mal), e/2, e/2, f, h (2-mal) Ecken: A, B, C, D (je 2-mal) Symbole: (wird 5-mal benötigt) Klebe diesen Zettel in dein Heft. erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 31 Flächeninhaltsberechnung Raute (Rhombus)! Beschrifte die dick markierten Linien! Schneide beide Flächen aus und zerschneide die Fläche entlang der markierten Linien. Lege die Teile so auf, dass ein Rechteck entsteht! Wie heißt die Länge dieses Rechtecks? Wie heißt die Länge dieses Rechtecks? _____________ _____________ Wie heißt die Breite dieses Rechtecks? Wie heißt die Breite dieses Rechtecks? _____________ _____________ Wie heißt die Flächenformel dieses Wie heißt die Flächenformel dieses Rechtecks? _________________ Rechtecks? _________________ Flächeninhaltsformel RAUTE (RHOMBUS): A = = _ Klebe die Teile, so wie du sie gelegt hast, in dein Heft. Schreibe die Formel darunter! erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 32 Umfangberechnung Raute (Rhombus)! Beschrifte die Seiten! Ziehe die Seiten einzeln mit einem bunten Stift nach. Notiere dir dabei immer, welche Seite du gerade nachgezogen hast. Seite Seite Seite 1. Seite 2. 3. 4. U Umfangsformel: U = + + + = _ Klebe diesen Zettel in dein Heft. Flächeninhaltsberechnung Trapez mit Mittellinie! Beschrifte die dick markierten Linien! Verwende für die Mittellinie zweimal den Buchstaben m (über und unter der Linie) und für die halbe Höhe h/2. Schneide die Fläche aus und zerschneide sie entlang der fett markierten Linien. Lege die Teile so auf, dass ein Rechteck entsteht! Wie heißt die Länge dieses Rechtecks? _____________ Wie heißt die Breite dieses Rechtecks? _____________ Wie heißt die Flächenformel dieses Rechtecks? ______________________________ Achtung! Du musst hier wahrscheinlich kürzen! 2. Flächeninhaltsformel TRAPEZ: A = _ Klebe die Teile, so wie du sie gelegt hast, in dein Heft. Schreibe die Formel darunter! Rechne die Beispiele Nr. ____ (Buch Seite ___) darunter ins Heft. erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 33 Quadrat einmal anders Beschrifte die zwei fett markierten Linien mit dem Buchstaben d (Diagonale) und schneide die Quadrate entlang dieser Strecke in zwei Hälften. Kannst du die vier Teile so zusammenlegen, damit daraus ein neues Quadrat entsteht? Wie lautet die Flächenformel dieses Quadrates? ___________________ Wie musst du die Flächenformel verändern, dass du den Flächeninhalt des gefärbten Quadrats erhältst: ________________ Schreibe die Überschrift FLÄCHENFORMEL QUADRAT in dein Heft, klebe die Teile, wie du sie aufgelegt hast, darunter und schreibe die Flächeninhaltsformel dazu. A = a² = erstellt von Mag. A. Mader u. G. Kilian für den Wiener Bildungsserver www.lehrerweb.at - www.kidsweb.at www.elternweb.at 34