Geometrie - Brichzin

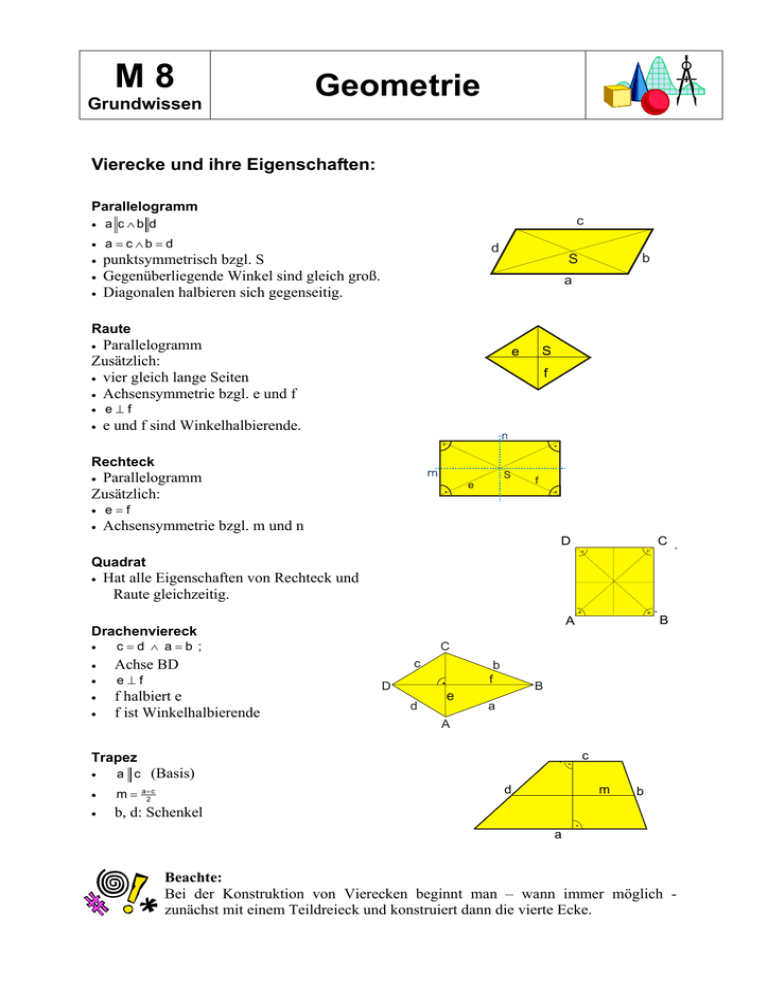
M8
Grundwissen
Geometrie
Vierecke und ihre Eigenschaften:
Parallelogramm
c
•
a c ∧b d
•
a = c ∧b = d
•
punktsymmetrisch bzgl. S
Gegenüberliegende Winkel sind gleich groß.
Diagonalen halbieren sich gegenseitig.
•
•
d
b
S
a
Raute
Parallelogramm
Zusätzlich:
• vier gleich lange Seiten
• Achsensymmetrie bzgl. e und f
•
•
e⊥f
•
e und f sind Winkelhalbierende.
S
e
f
.
.
Rechteck
•
e=f
•
Achsensymmetrie bzgl. m und n
.
S
e
f
.
D
C
Quadrat
•
d
Hat alle Eigenschaften von Rechteck und
Raute gleichzeitig.
c=d ∧ a=b ;
•
Achse BD
•
e⊥f
•
f halbiert e
f ist Winkelhalbierende
•
c
D
d
b
.
f
e
B
a
A
.
(Basis)
a c
•
m=
•
b, d: Schenkel
. c
d
a+c
2
B
C
Trapez
•
.
A
Drachenviereck
•
.
Parallelogramm
Zusätzlich:
•
m
a
b
.
Beachte:
Bei der Konstruktion von Vierecken beginnt man – wann immer möglich zunächst mit einem Teildreieck und konstruiert dann die vierte Ecke.
M8
Grundwissen
Geometrie
Tangente
Tangente t an einen Kreis in einem Punkt P:
•
Gerade, die den Kreis in dem Punkt P berührt;
•
Sie steht dort auf dem Radius r senkrecht.
Konstruktion einer Tangente t durch
einen Punkt
a) P auf der Kreislinie:
•
konstruiere eine Senkrechte zu r durch
P
b) P außerhalb des Kreises:
•
Verbinde M mit P
•
konstruiere den Thaleskreis über [MP]
•
die Schnittpunkte des Thaleskreises
mit k sind B1 und B2
•
PB1 und PB2 sind die Tangenten
r
.
Berührpunkt 2
M
P
Berührpunkt 1
δ
γ
Sehnenviereck
•
Alle Eckpunkte des Vierecks liegen auf einem Kreis.
•
α + γ = β + δ = 180°
Tangentenviereck
•
Alle vier Seiten sind Tangenten an denselben Kreis.
•
a+c =b+d
M
α
β
M8
Grundwissen
Geometrie
Flächenberechnungen
c
.
.
Parallelogramm:
ha
d
hb
AP = a ⋅ ha = b ⋅ hb ;
.
b
.
C
a
Dreieck:
AD = 21 ⋅ a ⋅ ha =
b
= 21 ⋅ b ⋅ hb =
= 21 ⋅ c ⋅ hc ;
.
=
hb
ha
Trapez:
A T = 21 ⋅ (a + c) ⋅ h =
.
A
. c
d
m
m ⋅ h ;
a
c
b
h
.
Volumenberechnung:
Prisma:
h
VPr = G ⋅ h ;
(Grundfläche mal Höhe)
G
.
.
a
hc
B