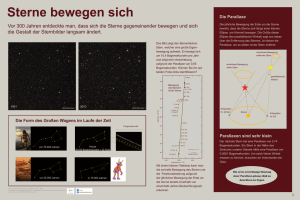
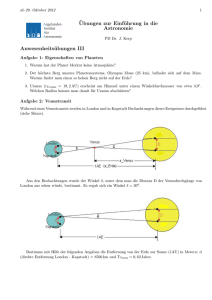
Aufgabe zur Entfernung von Fixsternen Mittelstufe

Der persönliche Schulservice im Internet
Hilfe im Schulalltag
SCHOOLSCOUT:
Astronomie
Thema:
Die Fixsterne (Teil 2)
TMD: 16131
Kurzvorstellung
des Materials:
Nach der theoretischen Vorbereitung für die Bestimmung einer
Parallaxe im 1. Teil von „Die Fixsterne“ kann das dort erlangte
Wissen nun anhand einer Himmelsaufnahme angewandt werden. Barnards Stern bietet hier ein ausgezeichnetes Beispiel
aufgrund seiner großen jährlichen Parallaxe.
Das Ihnen hier vorliegende Arbeitsblatt ist Teil einer Sammlung
für den Astronomieunterricht, welche Sie gratis beim Kauf eines Meade Schul-Teleskops erhalten.
Nähere Informationen finden Sie unter www.Schulteleskope.de
Übersicht über die
Teile
•
Information zum
Dokument
Ca. 6 Seiten, Größe ca. 334 KByte
SCHOOL-SCOUT –
schnelle Hilfe
per E-Mail
Bestimmung der Parallaxe und der Entfernung von Barnards
Stern
SCHOOL-SCOUT s Der persönliche Schulservice
Internet: http://www.School-Scout.de
E-Mail: [email protected]
SCHOOL-SCOUT s Der persönliche Schulservice
E-Mail: [email protected] s Internet: http://www.School-Scout.de s Fax: 02501/26048
Linckensstr. 187 s 48165 Münster
SCHOOL-SCOUT s Die Fixsterne (Teil 2)
Seite 2 von 6
Name:____________________________ Klasse:___________ Datum:________________
1. Im Arbeitsblatt „Die Fixsterne (Teil 1)“ für die Mittelstufe wurden die theoretischen
Grundlagen der parallaktischen Entfernungsbestimmung behandelt. Nun geht es darum, aus einer Fotografie eines Himmelsauschnitts die Entfernung eines Sterns zu
bestimmen.
Im Jahre 1916 entdeckte der amerikanische Astronom E. E. Barnard im Sternbild
Ophiuchus (Schlangenträger) einen Stern mit einer sehr hohen Eigenbewegung. Das
folgende Bild ist eine Überlagerung aus 5 Aufnahmen. Zu sehen ist der nach dem Entdecker benannte Stern „Barnards Pfeilstern“, wie er sich in den 5 Jahren von rechts
nach links bewegt hat:
SCHOOL-SCOUT s Der persönliche Schulservice
E-Mail: [email protected] s Internet: http://www.School-Scout.de s Fax: 02501/26048
Linckensstr. 187 s 48165 Münster
SCHOOL-SCOUT s Die Fixsterne (Teil 2)
Seite 3 von 6
Name:____________________________ Klasse:___________ Datum:________________
Die Aufnahmen wurden von rechts (Süden) nach links (Norden) am 17.10.1993,
12.05.1994, 22.09.1994, 01.05.1995 und am 10.10.1995 gemacht. Zur besseren Berechnung der Abstände wurden die mittleren Sternpositionen mit einem weißen Punkt
gekennzeichnet.
a. Warum beschreibt der Stern auf dem Foto keine Ellipse?
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
b. Zeichne den Bahnverlauf eines Sterns, so wie er von der Erde aus innerhalb
von zwei Jahren gesehen wird! Wie bewegt sich Barnards Stern?
c. Warum zeigen die Aufnahmen vom 17.10.1993 und vom 10.10.1995 die Bewegung des Sterns fast ohne parallaktische Einflüsse? Was ist mit den restlichen Aufnahmen?
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
SCHOOL-SCOUT s Der persönliche Schulservice
E-Mail: [email protected] s Internet: http://www.School-Scout.de s Fax: 02501/26048
Linckensstr. 187 s 48165 Münster
SCHOOL-SCOUT s Die Fixsterne (Teil 2)
Seite 4 von 6
Name:____________________________ Klasse:___________ Datum:________________
d. Berechne anhand des Bildes die Eigenbewegung µ des Sterns! Halte dabei den
Fehler möglichst klein. Die Kantenmaße des Bildes sind 4,0’ x 3,1’. Vergleiche mit dem Literaturwert µ = 10,3’’/a !
e. Bestimme die jährliche Parallaxe δ und die daraus resultierende Entfernung
1"⋅1 pc
r=
von Barnards Stern! Literaturwerte: δ = 0,5456’’ und r = 1.83 pc.
δ
SCHOOL-SCOUT s Der persönliche Schulservice
E-Mail: [email protected] s Internet: http://www.School-Scout.de s Fax: 02501/26048
Linckensstr. 187 s 48165 Münster
SCHOOL-SCOUT s Die Fixsterne (Teil 2)
Seite 5 von 6
Lösungen
1. Barnards Stern:
a. Würde der Stern fest im Raum stehen und keine Eigenbewegung besitzen, würde
man auf dem Bild die Positionen auf einer Ellipse wieder finden, da nur die jährliche Parallaxe zu sehen wäre. Weil aber gerade Barnards Stern eine sehr hohe Eigenbewegung hat, ist sein Weg durch den Raum geschlängelt, da sich seine geradlinige Bewegung und die Parallaxenbewegung überlagern.
b.
Barnards Stern bewegt sich wie in Bild 3.
c. Da nach einem Jahr die Erde wieder an derselben Stelle im All steht und somit der
Blickwinkel zum Stern derselbe ist wie ein Jahr zuvor, scheint der Stern wieder an
seinem ursprünglichen Ort zu stehen (abgesehen von seiner geradlinigen Bewegung durchs All). Die parallaktische Verschiebung ist dann nicht sichtbar. Man
kann sie am besten sehen, wenn man Aufnahmen im Abstand eines halben Jahres
macht. Es sind nur diese beiden Aufnahmen ohne parallaktischen Einfluss, da sie
fast genau ganzjährlich auseinander liegen. Da alle anderen Aufnahmen nicht exakt ganzjährliche Zeitspannen zwischen sich liegen haben, sind hier die parallaktischen Verschiebungen schon sichtbar.
d. Zuerst vernachlässigen wir die Bewegung von West nach Ost, da sich zeigt, dass
es in der Rechnung mit der gegebenen Fehlerquote keinen großen Einfluss hat.
Das Bild hat eine Höhe von 16,9cm. Das entspricht 4,0’ bzw. 240’’. Die Bewegung
des Sterns von Süd nach Nord in 2 Jahren (so wird der Fehler kleiner) beträgt
1,5cm. Damit folgt für die Bewegung:
µ=
240" 1,5cm
⋅
= 10,7" /a
16,9cm 2
SCHOOL-SCOUT s Der persönliche Schulservice
E-Mail: [email protected] s Internet: http://www.School-Scout.de s Fax: 02501/26048
Linckensstr. 187 s 48165 Münster
SCHOOL-SCOUT s Die Fixsterne (Teil 2)
Seite 6 von 6
Ein Grund für die Abweichung ist sicherlich die fehlerbehaftete Auswertung auf
dem Papier. Computergestütze Auswerteprogramme sind hier viel genauer. Trotzdem ist der errechnete Wert noch recht genau.
e. Um die Parallaxe zu berechnen, muss zuerst die große Halbachse der Ellipse bestimmt werden, da sie die Projektion der angenommenen kreisförmigen Erdbahn
um die Sonne ist. Dazu werden die beiden linken Aufnahmen (vom 01.05.1995 und
10.10.1995) benutzt, da sie fast genau ein halbes Jahr auseinander liegen. Man
misst den Abstand d der Verbindungslinie der beiden äußeren Aufnahmen
(17.10.1993 und 10.10.1995, die Aufnahmen ohne parallaktischen Einfluss) zur
Sternenposition am 01.05.1995. Es ergibt sich: d ≈ 1,0mm. Daraus folgt ein Abstand in Bogensekunden von:
2δ =
240"
⋅ 0,1cm = 1,42"
16,9cm
Damit ergibt sich eine Parallaxe von δ = 0,71" und mit r =
fernung: r =
1"⋅1 pc
= 1,41 pc .
0,71"
1"⋅1 pc
folgt für die Entδ
Die Abweichungen werden hier schon relativ groß, da mit sehr großen Fehlern
beim Ablesen gerechnet werde muss. Trotzdem liegen die Werte noch weit in der
gleichen Größenordnung und sind für die hier angewendete Methode recht gut.
SCHOOL-SCOUT s Der persönliche Schulservice
E-Mail: [email protected] s Internet: http://www.School-Scout.de s Fax: 02501/26048
Linckensstr. 187 s 48165 Münster