Fachwerkhaus - Auer Verlag

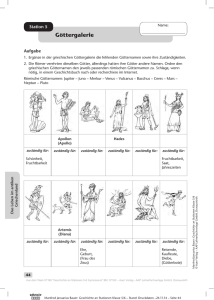
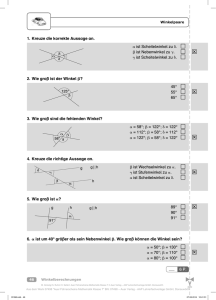
Name:
Station 7
Fachwerkhaus
Aufgabe 1
Aufgabe 2
Kennzeichne alle Winkel, die die gleiche Größe haben, mit der gleichen Farbe.
Aufgabe 3
Nenne weitere Dinge aus dem Alltag, bei denen Geraden auftreten, die sich schneiden.
Christian Wolf: Mathe an Stationen Spezial: Konstruktion in der Geometrie
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Grundkonstruktionen
Miss die Winkel in dem Bild und übertrage das Fachwerkhaus in dein Heft.
28
Aus dem Werk 07244 "Mathe an Stationen Konstruktion in der Geometrie" BN: 07244 – Auer Verlag - AAP Lehrerfachverlage GmbH, Donauwörth
07244.indb 28
27.01.2014 14:43:48
Name:
Station 8
Mittelsenkrechte konstruieren
Aufgabe 1
Zeichne hier jeweils eine Strecke AB mit der angegebenen Länge und konstruiere den Mittelpunkt
nur mit Zirkel und Lineal, also ohne Geodreieck.
b) 43 mm
c) 0,5 dm
Grundkonstruktionen
a) 3,7 cm
Aufgabe 2
Konstruiere eine Senkrechte zur Geraden g, die durch den Punkt P verläuft. Man sagt dazu auch:
„Fälle das Lot von P auf g.“ Vervollständige die hier begonnene Konstruktion.
Christian Wolf: Mathe an Stationen Spezial: Konstruktion in der Geometrie
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
P
B
A
g
Aufgabe 3
Zeichne eine beliebige Strecke schräg in dein Heft. Markiere nun mehrere Punkte, die nach Augenmaß auf der Mittelsenkrechten der Strecke liegen müssten.
Überprüfe deine Schätzung durch die Konstruktion der Mittelsenkrechten.
Wie genau hast du geschätzt?
29
Aus dem Werk 07244 "Mathe an Stationen Konstruktion in der Geometrie" BN: 07244 – Auer Verlag - AAP Lehrerfachverlage GmbH, Donauwörth
07244.indb 29
27.01.2014 14:43:48
Station 9
Name:
Höhen – Bestimmen von
Abständen
Aufgabe 1
Konstruiere auf einem Extrablatt ein Dreieck ABC mit den angegebenen Maßen. Mache zunächst
eine Planfigur. Zeichne die Höhen ha, hb und hc ein und miss sie.
a) a = 2 cm; b = 4 cm; c = 5 cm
b) b = 4,4 cm; a = 110°; g = 30°
c) a = 5,3 cm; b = 3,5 cm; a = 62°
Dreieckskonstruktionen
Aufgabe 2
Stefan möchte zur Insel im See schwimmen, weiß aber nicht, wie weit sie vom Ufer entfernt ist. Mit
einem Theodoliten (Winkelmessgerät im Gelände) peilt er das Ufer U der Insel von zwei 50 m auseinanderliegenden Punkten an und misst die Winkel a = 57° und b = 61°.
Wie weit muss Stefan schwimmen?
U
a
A
b
B
Christian Wolf: Mathe an Stationen Spezial: Konstruktion in der Geometrie
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
e
42
Aus dem Werk 07244 "Mathe an Stationen Konstruktion in der Geometrie" BN: 07244 – Auer Verlag - AAP Lehrerfachverlage GmbH, Donauwörth
07244.indb 42
27.01.2014 14:43:52
Name:
Station 10
Der Schwerpunkt des Dreiecks
Aufgabe 1
Zeichne ein beliebiges Dreieck auf ein Stück festeres Papier oder Pappe und schneide es aus.
a) Versuche dann, das Dreieck auf einer Linealkante zu balancieren. Markiere nur die Linien, bei
denen das Dreieck nicht heruntergefallen ist. Was kannst du beobachten?
Dreieckskonstruktionen
b) Versuche, das Dreieck auch auf einer Fingerspitze zu balancieren.
Aufgabe 2
Konstruiere den Schwerpunkt des Dreiecks ABC mit den Punkten A (2 | 4), B (6 | 2) und C (8,5 | 7,5).
y
10
9
Christian Wolf: Mathe an Stationen Spezial: Konstruktion in der Geometrie
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
8
7
6
5
4
3
2
1
0
x
1
2
3
4
5
6
7
8
9
10
43
Aus dem Werk 07244 "Mathe an Stationen Konstruktion in der Geometrie" BN: 07244 – Auer Verlag - AAP Lehrerfachverlage GmbH, Donauwörth
07244.indb 43
27.01.2014 14:43:53