Katheten und Hypotenusen

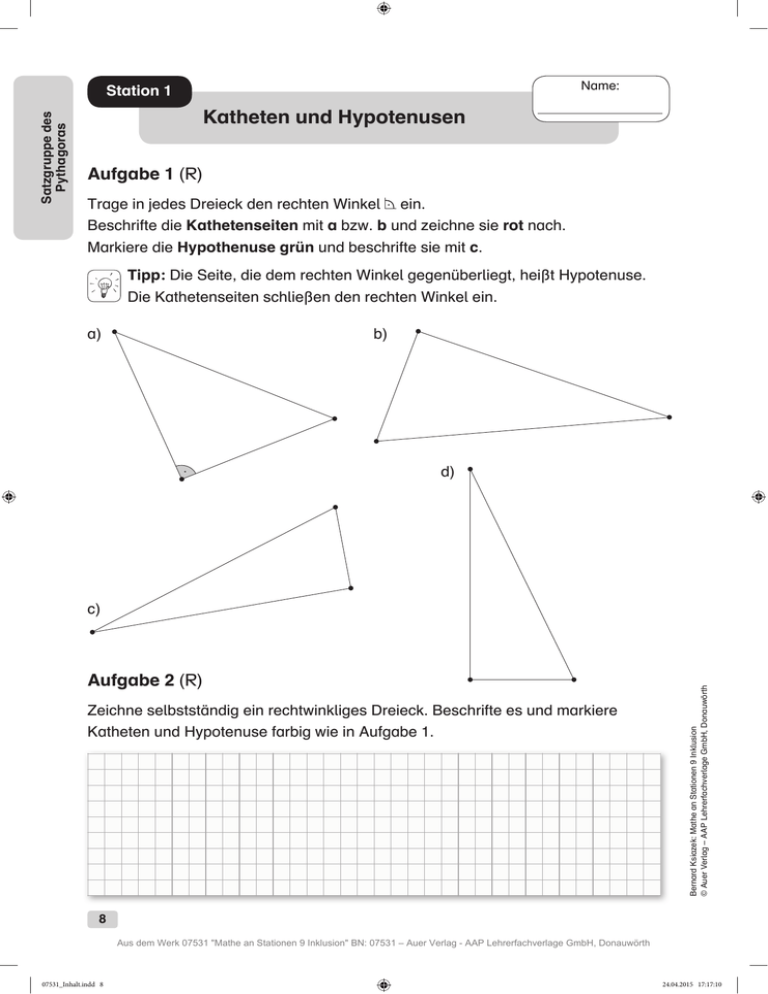
Name:
Satzgruppe des
Pythagoras
Station 1
Katheten und Hypotenusen
Aufgabe 1 (R)
Trage in jedes Dreieck den rechten Winkel ein.
Beschrifte die Kathetenseiten mit a bzw. b und zeichne sie rot nach.
Markiere die Hypothenuse grün und beschrifte sie mit c.
Tipp: Die Seite, die dem rechten Winkel gegenüberliegt, heißt Hypotenuse.
Die Kathetenseiten schließen den rechten Winkel ein.
a)
b)
d)
Aufgabe 2 (R)
Zeichne selbstständig ein rechtwinkliges Dreieck. Beschrifte es und markiere
Katheten und Hypotenuse farbig wie in Aufgabe 1.
Bernard Ksiazek: Mathe an Stationen 9 Inklusion
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
c)
8
Aus dem Werk 07531 "Mathe an Stationen 9 Inklusion" BN: 07531 – Auer Verlag - AAP Lehrerfachverlage GmbH, Donauwörth
07531_Inhalt.indd 8
24.04.2015 17:17:10
Name:
Station 2
Satzgruppe des
Pythagoras
Der Satz des Pythagoras
Aufgabe 1 (Z)
In einem rechtwinkligen Dreieck sind die Hypotenuse mit c und die Katheten mit a
und b bezeichnet. Daraus ergibt sich die Gleichung (der Satz von Pythagoras):
a2 + b2 = c.
Beschreibe in deinen Worten, was diese Gleichung bedeutet.
Aufgabe 2 (Z)
a) Markiere im Dreieck den rechten Winkel.
b) Zeichne die Hypotenuse c grün und die
Katheten a und b rot ein.
c) Die Hypotenuse soll aus den beiden
Kathetenlängen (a = 5 cm; b = 7 cm)
mithilfe des Satzes von Pythagoras
berechnet werden.
d) Berechne die fehlende Hypotenuse c
(wenn γ = 90°). a = 18 cm; b = 26 cm
Ergänze die Rechnung.
Bernard Ksiazek: Mathe an Stationen 9 Inklusion
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Tipp: Beachte, dass (5 cm)2
nicht 10 cm2 sind!
a2
+
(5 cm)2
+
+
b2
2
=
c2
=
c2
=
c2
=
c2
=
c
9
Aus dem Werk 07531 "Mathe an Stationen 9 Inklusion" BN: 07531 – Auer Verlag - AAP Lehrerfachverlage GmbH, Donauwörth
07531_Inhalt.indd 9
24.04.2015 17:17:11
Name:
Satzgruppe des
Pythagoras
Station 3
Pythagorasberechnung
Berechne mithilfe des Satzes von Pythagoras jeweils die fehlende Seitenlänge
im Dreieck. Runde das Ergebnis gegebenenfalls auf 2 Stellen nach dem Komma.
Schneide die Lösungskärtchen aus dem Anhang „Schneidevorlage Pythagoras­
berechnung“ aus und klebe sie an die richtige Stelle.
Wenn du alles richtig zugeordnet hast, erscheint ein entsprechendes Bild.
a = 5 cm; b = 11 cm;
γ = 90°
a = 14 cm; b = 8 cm;
γ = 90°
a = 75 m; b = 55 m;
γ = 90°
c=?
c=?
b = 36 cm; c = 40 cm;
α = 90°
b = 9 dm; c = 16 dm;
α = 90°
a = 22 cm; c = 29 cm;
β = 90°
a=?
a=?
b=?
a = 7 cm; b = 18 cm;
γ = 90°
a = 17 m; c = 24 m;
β = 90°
b = 62 dm; c = 83 dm;
α = 90°
c=?
b=?
a=?
c=?
Bernard Ksiazek: Mathe an Stationen 9 Inklusion
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
10
Aus dem Werk 07531 "Mathe an Stationen 9 Inklusion" BN: 07531 – Auer Verlag - AAP Lehrerfachverlage GmbH, Donauwörth
07531_Inhalt.indd 10
24.04.2015 17:17:11
Name:
Station 3
Satzgruppe des
Pythagoras
Anhang: Schneidevorlage
Pythagorasberechnung
✁
b ≈ 36,40 cm
b ≈ 29,41 m
c ≈ 19,31 cm
c ≈ 12,08 cm
a ≈ 53,81 cm
a ≈ 103,60 dm
Bernard Ksiazek: Mathe an Stationen 9 Inklusion
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
c ≈ 93,01 m
c ≈ 16,12 cm
a ≈ 18,36 dm
11
Aus dem Werk 07531 "Mathe an Stationen 9 Inklusion" BN: 07531 – Auer Verlag - AAP Lehrerfachverlage GmbH, Donauwörth
07531_Inhalt.indd 11
24.04.2015 17:17:12
1a)
Seite 8
1b)
b
c
a
a
c
b
1d)
Lösungen:
Satzgruppe des Pythagoras
Station 1: Katheten und Hypotenusen
rot = fette Linien
grün = gestrichelte Linien
1c)
b
c
c
a
a
b
2) Mehrere Lösungen möglich. Beispiele siehe Aufgabe 1.
Station 2: Der Satz des Pythagoras
Seite 9
1)Der Flächeninhalt des Hypotenusenquadrates ist genauso groß wie die Summe der Flächen­
inhalte der beiden Kathetenquadrate.
2 a), b)
rot = fette Linien2 c) a2 + b2 = c2
grün = gestrichelte Linien(5 cm)2 + (7 cm)2 = c2
b
Ka
ete
a
25 cm2 + 49 cm2 = c2
th
2 d) (18 cm)2 + (26 cm)2 = c2
Ka
e
et
th
1 000 cm2 = c2 74 cm2 = c2
Hypotenuse
31,62 cm ≈ c 8,60 cm ≈ c
c
Bernard Ksiazek: Mathe an Stationen 9 Inklusion
© Auer Verlag – AAP Lehrerfachverlage GmbH, Donauwörth
Station 3: Pythagorasberechnung
c2 = (5 cm)2 + (11 cm)2
c2 = 146 cm2
c ≈ 12,08 cm
c2 = (14 cm)2 + (8 cm)2
c2 = 260 cm2
c ≈ 16,12 cm
Seite 10
c2 = (75 m)2 + (55 m)2
c2 = 8 650 m2
c ≈ 93,01 m
a2 = (36 cm)2 + (40 cm)2 a2 = (9 dm)2 + (16 dm)2
a2= 2 896 cm2
a2 = 337 dm2
a ≈ 53,81 cm
a ≈ 18,36 dm
b2 = (22 cm)2 + (29 cm)2
b2= 1 325 cm2
b ≈ 36,40 cm
c2 = (7 cm)2 + (18 cm)2
c2 = 373 cm2
c ≈ 19,31 cm
a2 = (62 dm)2 + (83 dm)2
a2= 10 733 dm2
a ≈ 103,60 dm
b2 = (17 m)2 + (24 m)2
b2 = 865 m2
b ≈ 29,41 m
39
Aus dem Werk 07531 "Mathe an Stationen 9 Inklusion" BN: 07531 – Auer Verlag - AAP Lehrerfachverlage GmbH, Donauwörth
07531_Inhalt.indd 39
24.04.2015 17:17:37