Schwingungen und Wellen - lehrer.uni

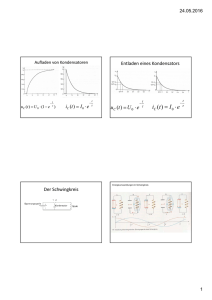
1. Klausur
Physik Grundkurs 13
17. Oktober 2000
Thema: Schwingungen und Wellen
Name: <PHYSIK_GRUNDKURS_13>
(Nr. <NR.>)
Verwende ggf.: g = 9, 81 sm2
Verr.Punkte
0. Für saubere und übersichtliche Darstellung, klar ersichtliche Rechenwege, sinnvoll gerundete Ergebnisse, Antworten in ganzen Sätzen und Zeichnungen mit spitzem Bleistift
erhalten Sie bis zu 4 Punkte.
1. a) Was versteht man unter einem verlustfreien elektromagnetischen Schwingkreis?
b) Ein verlustfreier Schwingkreis besteht aus einer idealen Spule der Induktivität
600 mH und einem Drehkondensator, dessen Kapazität stufenlos zwischen 2,00 F
und 5,00 F eingestellt werden kann.
Berechnen Sie die kleinste und die größte Frequenz des Schwingkreises.
c) Welche Kapazität hat der Drehkondensator im Schwingkreis aus Aufgabe b), wenn
die Schwingungsdauer 0,01 s beträgt?
2. Ein Körper K der Masse m = 800g wird an eine Schraubenfeder
N
angehängt. Die Federkonstante der Feder beträgt D 1 = 20 m .
Durch eine lotrecht nach unten wirkende Kraft wird nun der
Körper um s = 10,0 cm nach unten aus der Gleichgewichtslage
(siehe rechte obere Abbildung) ausgelenkt und dann frei gegeben.
Gleichzeitig wird die Zeitmessung gestartet (also t = 0).
a) Berechnen Sie die Verlängerung so der Feder vom unbelasteten
Zustand bis zur Gleichgewichtslage.
Wie groß ist die Schwingungsdauer T1 des Federschwingers?
b) Wie groß ist die Spannenergie der Feder im unteren Umkehrpunkt? In der Gleichgewichtslage ist die Feder um ca. 39 cm
ausgedehnt.
c) Zeichnen Sie ein t-s-Diagramm der ersten 2 Schwingungen
des Federschwingers.
d) Welche maximale Geschwindigkeit erreicht der Körper K?
e) Geben Sie die Gleichung für die Geschwindigkeit v(t) an.
Erläutern Sie Ihre Überlegungen.
f) Wie groß ist die Schwingungsdauer T2, wenn der Körper K
an die rechts abgebildete Federkombination gehängt wird
und lotrecht schwingt? Die Masse der Schraubenfedern ist
zu vernachlässigen.
g) Wie groß ist die Schwingungsdauer T3, wenn die beiden
(gleichartigen) Federn nicht parallel, sondern in Reihe
"geschaltet" werden?
...bitte wenden!
/4
/ 10
/ 20
Physik Grundkurs 13
17. Oktober 2000
3. Eine lineare Querwelle schreite mit der Geschwindigkeit c = 4 ms längs der x-Achse
eines Koordinatensystems fort. Der Erreger (x = 0) starte zur Zeit t = 0 seine "Sinusschwingung" nach unten mit der Frequenz f = 100 Hz und der Amplitude s = 3cm.
a) Zeichnen Sie die Welle zum Zeitpunkt t = 0, 020s im Bereich x [0; 12cm] .
b) Erstellen Sie das Diagramm der Teilchenbewegung bei x = 2,00 cm für 0 t 20ms .
Verr.Punkte
/8
4. Die folgende Abbildung zeigt den Anfang einer EXCEL-Tabelle zur Simulation einer
elektromagnetischen Schwingung. Das Schaubild ist aus den ersten 265 für die
Spannung am Kondensator (Uc) berechneten Werten gezeichnet worden.
a) Welche Formel könnte in der umrahmten Zelle "B14" stehen, um den dort angezeigten Wert −0, 059 zu berechnen?
b) Wie werden die Werte für die Ladung Q des Kondensators (Spalte D) berechnet?
c) Was für eine Art Schwingung scheint zu entstehen?
Erläutern Sie Ihre Überlegungen.
JOKER: Zeigen Sie, dass die gesamte Energie im ungedämpften Schwingkreis
E = 12 L Î 2 ist.
Punkte:
Durchschnitt:
(von 48)
Standardabweichung:
Notenpunkte:
Median:
Rückgabe am 18.10.2000
/6
/3
Physik Grundkurs 13
17. Oktober 2000
Erwartungshorizont
1. a) Ein geschlossener Leiterkreis aus einem Kondensator und einer Spule heißt Schwingkreis. Ist der ohmsche Widerstand der Spule und der Verbindungsdrähte vernachlässigbar klein, so spricht man von einem praktisch verlustfreien Schwingkreis.
b) Grundsätzlich gilt hier für die Frequenz:( )f =
1
LC
2
Analog f max =
L C max
1
L C min
2
2
=
0,600H 5 10 F
1
0,600H 2 10 −6 F
2
1/5
mit f =
1
T
C=
erhält man
=
2/5
3
10 3
2 1,2
Hz
145Hz
2/5
C=
c) ( ) nach C auflösen liefert:
2
2/2
Die minimale Frequenz erhält man bei maximaler Kapazität des Drehkondensators:
10 3
1
1
Also
fmin =
Hz 91, 9Hz
=
=
−6
2
Verr.Punkte
1
2 f2
T2
4
4
2
#
"
!
1/3
L
(0,01s) 2
4 2 0,600H
=
L
4, 2 F
%
#
2/3
$
"
2. a) In der Gleichgewichtslage sind die Gewichtskraft des Körpers und die Federspannkraft gleich groß:
F G = F F , also m g = D 1 s o , aufgelöst nach so: s o =
&
&
mg
D1
'
=
N
0,800kg 9,81 kg
(
0, 39m
N
20 m
b) Für den voll ausgelenkten Körper beträgt die Dehnung der Feder s o + s 1
2
N
1
1
Spannenergie: E = 2 D 1 (s o + s 1 ) 2 2 20 m (0, 49m )
2, 4 J
*
0, 49m.
3/3
-
+
,
,
c) Das Zeit-Elongationsgesetz ist: s = s sin( t)
mit s = 0, 10m und
/
.
T=
D1
m
=
20 N
m
0,800kg
2/2
)
= 5 s −1 , also s = 0, 1 sin(5t)
2/5
0
Die ersten 2 Schwingungen benötigen also die Zeit
Maßstab von z.B. 1s 5cm an (siehe Abbildung)
4
5
1
Sekunden. Es bietet sich ein
2
3/5
d) Die maximale Geschwindigkeit hat der Körper K beim Durchgang durch die Gleichgewichtslage. Für diese Lage gilt:
1
2m
3
(v max ) 2 = 12 D s 2 also v max = s
3
3
D1
m
= 0, 10m
3
N
20 m
0,800kg
= 0, 50 ms
2/2
e) Das Zeit-Geschwindigkeits-Gesetz ist die Ableitung des Zeit-Elongations-Gesetzes.
.
v(t) =s (t) =
s cos( t) = 0, 5 cos(5t)
2/2
f) Die Federkonstante bei Parallelschaltung erhält man aus: D 2 = D 1 + D 1 = 40 mN .
Die Schwingungsdauer T2 berechnet sich also:
1/3
4
T2 = 2
7
m
D2
5
5
=2
5
6
0,800kg
8
N
40 m
9
0, 88 s
2/3
Physik Grundkurs 13
17. Oktober 2000
g) Bei Reihenschaltung ergibt sich
Entsprechend gilt: T 3 = 2
:
1
D3
=
1
D1
=2
m
D3
+
1
D 1 , also
0,800kg
Verr.Punkte
3/3
1, 8 s
N
10 m
:
D 3 = 12 D 1
;
3. a) Da sich die Welle mit der Geschwindigkeit c = 4 ms in x-Richtung ausbreitet, hat ihr
Anfang in der Zeit t = 0, 020s die Strecke s = c t = 0, 08 m zurückgelegt.
Die Frequenz des Erregers beträgt f = 100 Hz, es gab also in der Zeit t = 0, 020s exakt zwei Schwingungen. Da nach unten begonnen wurde und die Amplitude s = 3cm
beträgt, ist die Gleichung der zu skizzierenden Schwingung:
t −0, 03 sin(200 t)
<
=
>
?
@
4/4
b) Die Stelle x = 2,00 cm erreicht die Welle nach 5 Millisekunden. Dann gibt es alle 10
Millisekunden eine komplette Schwingung, es bleibt also bis zur Zeit 20ms Zeit für
1,5 Schwingungen.
Die Gleichung der (ab t = 0,005 s) zu skizzierenden Schwingung lautet also:
t −0, 03 sin(200 (t − 0, 005))
A
B
C
B
4/4
4. a) Da hier schrittweise I und Uc berechnet werden, erhält man natürlich Ineu = Ialt + dI,
die Formel lautet also: "= B13 + E13"
Q
Uc
2/2
b) Am Kondensator gilt. C = , also berechnet sich Q:
Q = C Uc
C = 2 F findet man in C4, Uc steht jeweils in der gleichen Zeile.
2/2
c) Es handelt sich um eine gedämpfte Schwingung, da die Amplitude abnimmt. Hier
wird der ohmsche Widerstand nicht vernachlässigt wird.
2/2
D
E
JOKER:
E ges =
1
2
2
2
C U cos 2 ( t) + 12 L I sin 2 ( t)
L
2
2
wegen U = I
C und sin ( t) + cos ( t) = 1 folgt:E ges =
G
F
F
F
G
H
H
H
G
H
G
1
2
2
L I .
H
H
3/3