Kurzlehrplan Mathematik (Klassen 5-9) - IServ mercator
Werbung
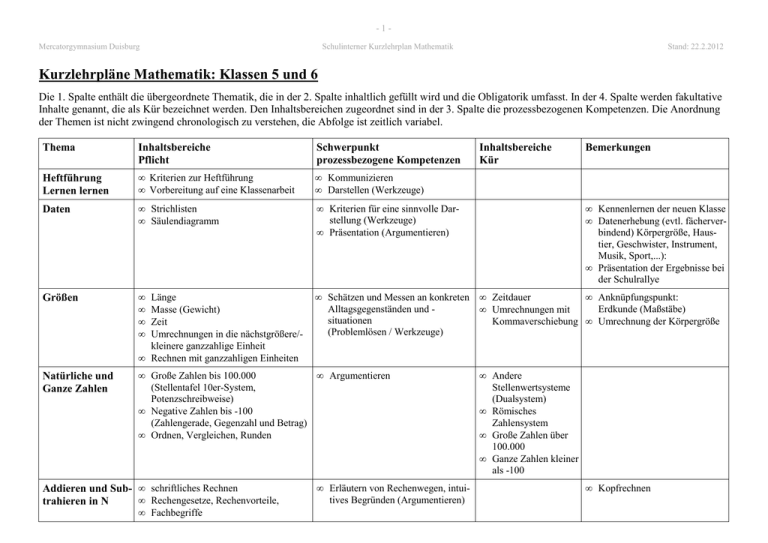
-1Mercatorgymnasium Duisburg Schulinterner Kurzlehrplan Mathematik Stand: 22.2.2012 Kurzlehrpläne Mathematik: Klassen 5 und 6 Die 1. Spalte enthält die übergeordnete Thematik, die in der 2. Spalte inhaltlich gefüllt wird und die Obligatorik umfasst. In der 4. Spalte werden fakultative Inhalte genannt, die als Kür bezeichnet werden. Den Inhaltsbereichen zugeordnet sind in der 3. Spalte die prozessbezogenen Kompetenzen. Die Anordnung der Themen ist nicht zwingend chronologisch zu verstehen, die Abfolge ist zeitlich variabel. Thema Inhaltsbereiche Pflicht Schwerpunkt prozessbezogene Kompetenzen Heftführung Lernen lernen • Kriterien zur Heftführung • Vorbereitung auf eine Klassenarbeit • Kommunizieren • Darstellen (Werkzeuge) Daten • Strichlisten • Säulendiagramm • Kriterien für eine sinnvolle Darstellung (Werkzeuge) • Präsentation (Argumentieren) Größen • • • • Länge Masse (Gewicht) Zeit Umrechnungen in die nächstgrößere/kleinere ganzzahlige Einheit • Rechnen mit ganzzahligen Einheiten • Schätzen und Messen an konkreten • Zeitdauer • Anknüpfungspunkt: Alltagsgegenständen und Erdkunde (Maßstäbe) • Umrechnungen mit situationen Kommaverschiebung • Umrechnung der Körpergröße (Problemlösen / Werkzeuge) Natürliche und Ganze Zahlen • Große Zahlen bis 100.000 • Argumentieren (Stellentafel 10er-System, Potenzschreibweise) • Negative Zahlen bis -100 (Zahlengerade, Gegenzahl und Betrag) • Ordnen, Vergleichen, Runden Addieren und Sub- • schriftliches Rechnen • Rechengesetze, Rechenvorteile, trahieren in N • Fachbegriffe • Erläutern von Rechenwegen, intuitives Begründen (Argumentieren) Inhaltsbereiche Kür Bemerkungen • Kennenlernen der neuen Klasse • Datenerhebung (evtl. fächerverbindend) Körpergröße, Haustier, Geschwister, Instrument, Musik, Sport,...): • Präsentation der Ergebnisse bei der Schulrallye • Andere Stellenwertsysteme (Dualsystem) • Römisches Zahlensystem • Große Zahlen über 100.000 • Ganze Zahlen kleiner als -100 • Kopfrechnen -2Mercatorgymnasium Duisburg Thema Inhaltsbereiche Pflicht Multiplizieren und • schriftliches Rechnen • Rechengesetze, Rechenvorteile, Dividieren in N Schulinterner Kurzlehrplan Mathematik Schwerpunkt prozessbezogene Kompetenzen Stand: 22.2.2012 Inhaltsbereiche Kür Bemerkungen • Erläutern von Rechenwegen, intuitives Begründen (Argumentieren) • Verbindung aller Grundrechenarten („Vorfahrtsregeln“, Rechenreihenfolge • Fachbegriffe) Geometrische Grundbegriffe • Strecke, Gerade, Halbgerade, Kreis • senkrecht. waagerecht, achsensymmetrisch, punktsymmetrisch, Winkel • Koordinatensystem (1. Quadrant) Flächeninhalt und • Flächeninhalt und Umfang von Quadrat, Rechteck, Dreieck, Umfang I Parallelogramm und zusammengesetzten Figuren • Flächeneinheiten, • Umrechnungen • Formeln für Fläche und Umfang • exaktes Zeichnen und Messen (Werkzeuge) • Konstruktion mit Geodreieck (Werkzeuge) • optische Täuschungen zu senkrecht und waagerecht • sinnvolles Überprüfen durch Probieren (Problemlösen) • Vernetzung mit den Kapiteln „Größen“ (Argumentieren) • Flächen mit gleichem Umfang vergleichen Addition / Multiplikation in Z • schriftliches Rechnen • Rechengesetze, Rechenvorteile, Klammern • Erläutern von Rechenwegen, intui- • Subtraktion/Division • Kontospiel tives Begründen (Argumentieren) in Z * Geometrische Figuren • Körper, Netze und Schrägbilder • exaktes Zeichnen und Messen • Platonische Körper (Werkzeuge) • Oberfläche und Volumen von Quadern • Zusammengesetzte • Schätzen, Messen, Vergleichen und Körper • Volumeneinheiten Validieren (Modellieren) Teilbarkeit • Teiler und Vielfache • Teilbarkeitsregeln für 2, 3, 5, 10 • Primzahlen • Überprüfen durch Probieren (Problemlösen) • verallgemeinern und argumentativ begründen (Argumentieren) • Einsatz von Klickies • Körper basteln (exaktes Arbeiten) • Bau Was (MUED) • Primfaktorzerlegung, ggf. auch nach Einführung der Brüche: ggT, kgV • Teilbarkeitsregeln für • Primzahlsieb • Der Zahlenteufel 4, 6, 8, 9 -3Mercatorgymnasium Duisburg Schulinterner Kurzlehrplan Mathematik Stand: 22.2.2012 Thema Inhaltsbereiche Pflicht Schwerpunkt prozessbezogene Kompetenzen Brüche • • • • • Brüche im Alltag (Modellieren / • Periodische Problemlösen) Dezimalzahl • Gebrauch von Geodreieck und Zirkel (Werkzeuge) • Herstellen von Bruchteilen • Anwendung Winkel (Messen und Zeichnen) • Kopfrechnen Addition und Sub- • gleichnamige Brüche addieren u. subtrahieren traktion • Wiederaufgreifen von Einführungsbeispielen (Modellieren) • Schwerpunkt: Training! • Wiederholung der Rechenregeln für ganze Zahlen sinnvoll* Multiplikation und • Rechenregeln • schriftliches Rechnen mit einfachen Division • Anteilsbestimmung als Grundvorstellung (Argumentieren) Darstellung Erweitern, Kürzen Vergleichen, Ordnen Umwandeln von endlichen Dezimalzahlen, Brüchen und Prozentzahlen • gleichnamig Machen von einfachen Brüchen • Erarbeitung und Anwendung von Rechengesetzen Inhaltsbereiche Kür • * Bemerkungen • Schwerpunkt: Training! Brüchen Dezimalzahlen • Ordnen, Vergleichen, Runden • Grundrechenarten mit endlichen Dezimalzahlen. • Erläutern von Rechenwegen, intui- • Dreisatz tives Begründen (Argumentieren) Statistik • absolute/relative Häufigkeit • Arith. Mittel, Median • Kreisdiagramm, Säulendiagramm • Präsentationstechniken und –kriterien erarbeiten, umsetzen und bewerten (Argumentieren) • evt. Einsatz einer Tabellenkalkulation (Werkzeuge) • Boxplot Beziehungen und Veränderungen beschreiben • Muster erkunden • Diagramme lesen • gängige Maßstabsverhältnisse nutzen • Erläutern von mathematischen Sachverhalten (Verbalisieren) • Fibonacci * • evtl. Datenerhebung in GA • Anwendung Winkel (Zeichnen und Messen) Subtraktion / Division von negativen Zahlen im KLP nicht vorgeschrieben, dennoch hier sinnvoll, da nicht alle Schulbücher (Fokus, Lambacher Schweizer) das Rechnen mit rationalen Zahlen in der 7. Klasse aufgreifen -4Mercatorgymnasium Duisburg Schulinterner Kurzlehrplan Mathematik Stand: 22.2.2012 Kurzlehrpläne Mathematik: Klassen 7 und 8 Thema Inhaltsbereiche Pflicht Schwerpunkt prozessbezogene Kompetenzen Inhaltsbereiche Kür Bemerkungen Zuordnungen • verschiedene Darstellungsformen (Tabelle, Graph, Diagramm, Situation) • proportionale Zuordnungen, • antiproportionale Zuordnungen • Dreisatz • Anwendung (z.B. Handytarif) (Modellieren) • zielgerichtetes Einsetzen und Bewerten der Darstellungsformen (Argumentieren) • Zusammenhänge zwischen Größen verbalisieren (Argumentieren) • Produktgleichheit, Quotientengleichheit • Tabellenkalkulation zum Visualisieren Prozent- und Zinsrechnung • Grundwert, Prozentsatz, Prozentwert • Tageszinsen, • Angebote (z.B. Werbeprospekte), Monatszinsen Rechnungen (Modellieren) • fehlerhafte Zeitungstexte (Argumentieren) • Benennen der gegeben Größen, Beschreibung des Lösungsweges (Kommunizieren) • Einsatz von Taschenrechner und Tabellenkalkulation (Werkzeuge) 1) Es besteht die Möglichkeit, zum Einstieg einfache Gleichungen zu behandeln. Vorteile: Die Schüler gewöhnen sich an den Einsatz von Variablen; bei den folgenden Themen kann systematischer „rückwärts" gerechnet werden; in der Prozentrechnung kann nach den gesuchten Größen umgeformt werden, ohne mehrere Formeln zu verwenden. 2) Die beiden Themen können vertauscht werden. Vorteile: Im vorliegenden Fall kann bei der Prozentrechnung bereits der Dreisatz angewendet werden; im umgekehrten Fall üben die Schüler den Umgang mit Formeln (Benennen der gegebenen Größen) Prozentdreieck (siehe LS 7) Stochastik I • Datenerhebungen und –aufbereitung • Wahrscheinlichkeiten in (auch: Boxplots!) Kontexten (Modellieren) • Wahrscheinlichkeitsbegriff • Chancen einschätzen und Risiken bewerten • Standardmodelle zur Beschreibung (Problemlösen) (Urnenmodelle) • zweistufige Zufallsexp. (Pfadregeln) • Präsentation von Datenerhebungen (Argumentieren) • Simulation Hier kann Stochastik eingefügt • Gegenereignis werden. Vorteil: schließt an • mehrstufige Zufallsexperimente Prozentrechnung und mathematische Darstellungen an -5Mercatorgymnasium Duisburg Schulinterner Kurzlehrplan Mathematik Stand: 22.2.2012 Thema Inhaltsbereiche Pflicht Schwerpunkt prozessbezogene Kompetenzen Inhaltsbereiche Kür Bemerkungen Terme 1 • Terme aufstellen aus Sachzusammenhängen • Terme berechnen • Terme umformen • Muster erkennen und durch Terme beschreiben (Problemlösen) • mit Termen Fragestellungen beschreiben und lösen (Modellieren) • Termspiele und Zahlenrätsel (Problemlösen) • Bezug zu Gleichungen • rückwärts rechnen • Rechnen mit Potenzen (2 und 3) • Wortform von Termen Hier bietet sich die systematische Einführung von Strategien zum Problemlösen bzw. Modellieren an. Gleichungen 1 • Aufstellen von Gleichungen • Lösen von Gleichungen (Lösen durch Probieren, systematisches Lösen linearer Gleichungen) • Altersaufgaben, Zahlenrätsel (Problemlösen/Argumentieren) • Bewegungsaufgabe n (Begegnen, Einholen) (Modellieren) • LGS • zeichnerisches Lösen (Vernetzung mit linearen Funktionen) • rein quadratischeAufgaben -6Mercatorgymnasium Duisburg Schulinterner Kurzlehrplan Mathematik Stand: 22.2.2012 Thema Inhaltsbereiche Pflicht Schwerpunkt prozessbezogene Kompetenzen Inhaltsbereiche Kür Bemerkungen Geometrie • Winkelsätze • Winkelbeziehungen an Geradenkreuzungen • Konstruktion von Dreiecken • spezielle Dreiecke • Satz des Thales • Kongruenzsätze • Konstruieren per Hand , Geometriesoftware) (Werkzeuge) • Verbalisieren der Konstruktion (Problemlösen) • Beweis der Innenwinkelsumme im Dreieck (Argumentieren) • n-Ecke • Außenwinkelsatz • besondere Linien im Dreieck • Inkreis/Umkreis Alternative: Einstieg über Eigenschaften besonderer Dreiecke / Konstruktion von Dreiecken Vorteil: die Schüler entdecken die Kongruenzsätze und können schnell Anwendungsaufgaben lösen. Nachteil: Winkelsummensatz wird benötigt und kann ohne Winkelbeziehungen nicht bewiesen werden; Winkelsummensatz durch "Zerreißprobe" aber möglich! Lineare Funktionen • Funktionen als eindeutige Zuordnungen • allgemeine Geradengleichung y=mx+b • Zeichnen von Geraden • Anwendungen • Tarife visualisieren (Modellieren) • Graphen beschreiben und interpretieren (Argumentieren) • Bestimmen von Geradengleichungen aus 2 Punkten • abschnittsweise definierte Funktionen Terme 2 • Multiplikation von Summen (geometrische Veranschaulichung) • Binomische Formeln • Faktorisieren • Erläutern an Flächenbeispielen (Argumentieren) • Pascalsches Dreieck Flächen und Volumina • Flächenberechnung und Umfang von Kreisen und zusammengesetzten Figuren • Volumina und Oberfläche von Prismen und Zylindern • Erkunden der Kreiszahl Pi (Problemlösen) • Rückführung auf bekannte geometrische Figuren (Problemlösen) • n-Ecke • Bogenmaß -7Mercatorgymnasium Duisburg Schulinterner Kurzlehrplan Mathematik Thema Inhaltsbereiche Pflicht Reelle Zahlen • Wurzeln als Umkehrung des • Quadratwurzeln als • Einsatz des TR Strecken Potenzierens (Schwerpunkt (anwendungsbezogenes Runden) Quadratwurzeln) (Werkzeuge) • Heronverfahren oder Intervall• Berechnen und Überschlagen von einfachen Quadratwurzeln schachtelung • Beweis Irrationali• Charakterisieren und Vergleich von tät von Wurzel 2 rationalen und irrationalen Zahlen • Rechnen mit Quadratwurzeln Lineare • Aufstellen von Gleichungen und Gleichungssysteme Gleichungssystemen mit zwei Variablen • Lösen von Gleichungen (Lösen durch Probieren, zeichnerisches Lösen, algebraische(s) Lösungsverfahren) • Probe als Rechenkontrolle • Anwendungen Stochastik II • Analyse grafischer statistischer Darstellungen • Bedingte Wahrscheinlichkeit (Baumdiagramm, Vierfeldertafel) Schwerpunkt prozessbezogene Kompetenzen Stand: 22.2.2012 Inhaltsbereiche Kür • Schnittpunktbestimmung • Verschiedene (Zeichnung, Funktionsplotter, Verfahren Geometriesoftware) (Gleichsetzungs-, (Werkzeuge) Additions- und Einsetzungsverfahren) • Bewegungsaufgaben (Begegnen, Einholen) • Gleichungssysteme (Modellieren) mit drei oder mehr Variablen • Umkehraufgabe (Realsituation zu einer Gleichung finden) (Modellieren) • Beurteilen und Bewerten (Argumentieren) • Darstellen und Manipulieren von Diagrammen (Werkzeuge) • Realsituationen übersetzen (Modellieren) Bemerkungen -8Mercatorgymnasium Duisburg Schulinterner Kurzlehrplan Mathematik Stand: 22.2.2012 Kurzlehrpläne Mathematik: Klasse 9 Thema Inhaltsbereiche Pflicht Schwerpunkt Prozessbezogene Kompetenzen Inhaltsbereiche Kür Bemerkungen Funktionen I • quadratische und lineare Funktionen (Darstellungsformen: Text, Graf, Tabelle, Term • quadratische Funktion (Scheitelpunktsform, Nullstellenform, allgemeine Form) • einfache quadratische Gleichungen • Lösungswege, Problemlösestrategien vergleichen (Problemlösen) • Benennen von Vor- und Nachteilen der verschiedenen Darstellungsformen (Argumentieren) • weitere Lösungsverfahren • Linearfaktorzerlegung mit Polynomdivision hier nur quadratische Gleichungen, auf die ein Lösungsverfahren (z.B. Faktorisieren, pq-Formel) unmittelbar angewendet werden kann, keine Wurzelund Bruchgleichungen Geometrie I • Ähnlichkeit, Verkleinern, Vergrößern ( Beschreibung und Begründung von Ähnlichkeitsbeziehungen geometrischer Objekte) • Analyse von Sachzusammenhängen (Problemlösen) • Strahlensätze Verbindung zur Algebra Vernetzung mit Statistik (Manipulation von Grafiken) Geometrie II • Satz des Pythagoras • Satz des Thales • Definition von Sinus. Kosinus und Tangens • Zerlegen in Teilprobleme (Problemlösen) • Vernetzung mit Algebra (Argumentieren) • Realsituationen übersetzen (Modellieren) • weitere Sätze aus der Satzgruppe des Pythagoras • Einheitskreis Satz des Thales: siehe Kl. 7/8 Kür Geometrie III • Körper (Pyramide, Kegel, Kugel) • Oberfläche und Volumen (Pyramide, Kegel, Kugel) • Zerlegen in Teilprobleme (Problemlösen) • Erstellung von Netzen und Körpern (Konstruktion) • Cavalieri Netze von Zylinder, Pyramide, Kegel können z.B. in Klasse 5 vorbereitet werden Quadratische Funktionen -9Mercatorgymnasium Duisburg Funktionen II (exponentielle und periodische Funktionen Schulinterner Kurzlehrplan Mathematik • Zahlen in Zehnerpotenzschreibweise lesen und schreiben • Potenzen mit ganzzahligen Exponenten • Zinseszins als Beispiel für exponentielles Wachstum • Sinusfunktion zur Beschreibung einfachen periodischer Vorgänge (Wertetabelle, Graf, Term, Wort) Stand: 22.2.2012 • Modellieren • Werkzeuge • Potenzgesetze • Logarithmus zur Bestimmung der Zeit • Ausblick auf stetiges exponentielles Wachstum Vernetzung mit den linearen und quadratischen Funktionen Anknüpfungspunkt: Physik (Schwingungen)