Gesamtschule Hünxe - der Gesamtschule Huenxe
Werbung
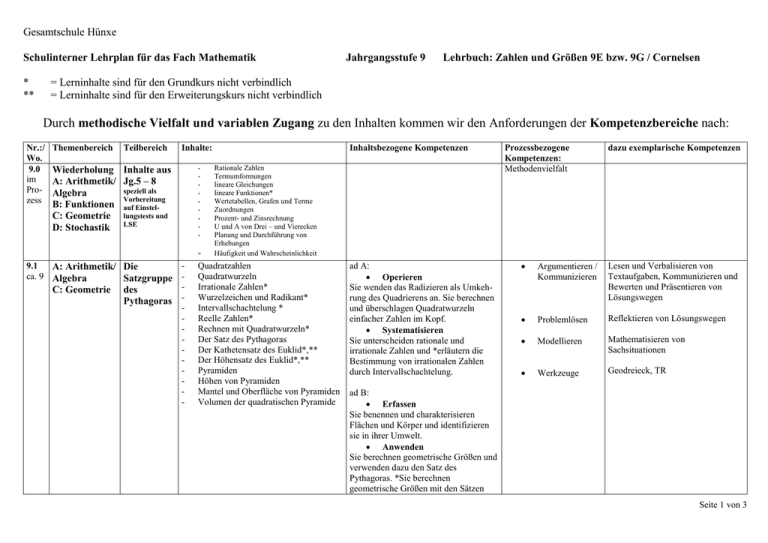
Gesamtschule Hünxe Schulinterner Lehrplan für das Fach Mathematik * ** Jahrgangsstufe 9 Lehrbuch: Zahlen und Größen 9E bzw. 9G / Cornelsen = Lerninhalte sind für den Grundkurs nicht verbindlich = Lerninhalte sind für den Erweiterungskurs nicht verbindlich Durch methodische Vielfalt und variablen Zugang zu den Inhalten kommen wir den Anforderungen der Kompetenzbereiche nach: Nr.:/ Wo. 9.0 im Prozess Themenbereich Teilbereich Inhalte: Wiederholung Inhalte aus A: Arithmetik/ Jg.5 – 8 speziell als Algebra Vorbereitung B: Funktionen auf EinstelC: Geometrie lungstests und D: Stochastik LSE 9.1 A: Arithmetik/ Die ca. 9 Algebra Satzgruppe C: Geometrie des Pythagoras - - Inhaltsbezogene Kompetenzen Rationale Zahlen Termumformungen lineare Gleichungen lineare Funktionen* Wertetabellen, Grafen und Terme Zuordnungen Prozent- und Zinsrechnung U und A von Drei – und Vierecken Planung und Durchführung von Erhebungen Häufigkeit und Wahrscheinlichkeit Quadratzahlen Quadratwurzeln Irrationale Zahlen* Wurzelzeichen und Radikant* Intervallschachtelung * Reelle Zahlen* Rechnen mit Quadratwurzeln* Der Satz des Pythagoras Der Kathetensatz des Euklid*,** Der Höhensatz des Euklid*,** Pyramiden Höhen von Pyramiden Mantel und Oberfläche von Pyramiden Volumen der quadratischen Pyramide ad A: Operieren Sie wenden das Radizieren als Umkehrung des Quadrierens an. Sie berechnen und überschlagen Quadratwurzeln einfacher Zahlen im Kopf. Systematisieren Sie unterscheiden rationale und irrationale Zahlen und *erläutern die Bestimmung von irrationalen Zahlen durch Intervallschachtelung. Prozessbezogene Kompetenzen: Methodenvielfalt dazu exemplarische Kompetenzen Argumentieren / Kommunizieren Lesen und Verbalisieren von Textaufgaben, Kommunizieren und Bewerten und Präsentieren von Lösungswegen Problemlösen Reflektieren von Lösungswegen Modellieren Mathematisieren von Sachsituationen Werkzeuge Geodreieck, TR ad B: Erfassen Sie benennen und charakterisieren Flächen und Körper und identifizieren sie in ihrer Umwelt. Anwenden Sie berechnen geometrische Größen und verwenden dazu den Satz des Pythagoras. *Sie berechnen geometrische Größen mit den Sätzen Seite 1 von 3 des Euklid Darstellen Stellen lineare Funktionen mit eigenen Worten, in Wertetabellen, als Graphen und mithilfe der Funktionsgleichung dar. Interpretieren Deuten die Parameter der Funktionsgleichungen in der graphischen Darstellung und nutzen dies in Anwendungssituationen Anwenden Wenden lineare Funktionen zur Lösung außer- und innermathematischer Problemstellungen an 9.2a A: Arithmetik/ Lineare ca. 6 Algebra Funktionen ** Der E-Kurs behandelt an dieser Stelle nur noch die Themen, die aus Jahrgang 8 fehlen 9.2b A: Arithmetik/ Lineare * Algebra Gleichungs- ca. 6 systeme* 9.3 ca.8 C: Geometrie Kreise und Kreiskörper - lin. Gleichungen mit zwei Variablen* nicht lin. Gleichungen mit zwei Variablen* graph. Lösungen von Gleichungssystemen* rechnerische Lösung von Gleichungssystemen* Gleichsetzungsverfahren Einsetzungsverfahren* Add./Subtr.-Verfahren* Lin. Gleichungssysteme mit mehr als zwei Variablen* Die Kreiszahl л Bestimmung von л Umfang des Kreises Flächeninhalt des Kreises Kreisring Kreisausschnitt* Kreisbogen* Netze von Zylinder, Kegel und Pyramide Schrägbilder von Zylinder, Kegel und Pyramide* Volumen des Zylinders Operieren Lösen linearer Gleichungssysteme mit zwei Variablen sowohl durch Probieren als auch algebraisch und grafisch. Anwenden Verwenden ihre Kenntnisse über lineare Gleichungssysteme mit zwei Variablen zur Lösung inner- und außermathematischer Probleme. Messen Schätzen und Bestimmen Umfänge und Flächeninhalte von Kreisen und zusammengesetzten Flächen sowie Oberflächen und Volumina von Zylindern, Pyramiden und Kegeln. Erfassen Benennen und charakterisieren Körper und identifizieren sie in ihrer Umwelt. Konstruieren Skizzieren Schrägbilder, entwerfen Netze von Zylindern Kegeln und Argumentieren/ Kommunizieren Verbalisieren mathematische Zusammenhänge mit eigenen Worten *Präsentieren Problembearbeitungen in vorbereiteten Vorträgen *Vernetzen Begriffe und Verfahren Problemlösen Erkunden und Reflektieren Lösungswege und *Strategien Modellieren Übersetzen Realsituationen in Modelle Finden zu einem Modell die passende Realsituation Werkzeuge Argumentieren/ Kommunizieren Nutzen Funktionenplotter* Wählen geeignete Medien zur Dokumentation und Präsentation Lesen und Informationsbeschaffung aus Sachaufgaben und z.B. Zeitungsberichten Problemlösen Anwenden von „Vor- und Rückwärtsarbeiten“ als Lösungsstrategie Modellieren Mathematisieren von Realsituationen Werkzeuge TR, Geodreieck Argumentieren/ Kommunizieren Ziehen Informationen aus Texten *Verbalisieren Zusammenhänge *Überprüfen Problembearbeitungen nutzen mathematisches Wissen und *Symbole für Begründungen und Argumentationsketten Problemlösen Erkunden und Reflektieren Lösungswege und *Strategien Modellieren Erkunden und Reflektieren Lösungswege und *Strategien Seite 2 von 3 9.6 ca.4 C: Geometrie 9.7 D: Stochastik ca. 4 Ähnlichkeit Daten und Zufall - Oberfläche des Zylinders Volumen des Kegels Oberfläche des Kegels - Ähnlichkeit Vergrößern und Verkleinern Ähnlichkeitsfaktor Zentrische Streckung* Strahlensätze* Anwendungen zum Strahlensatz* - relative Häufigkeit arithmetisches Mittel Zentralwert Abweichung vom arithmetischen Mittel* Streuung und Streumaß* durchschnittliche Streuung* Pyramiden und stellen die Körper her. Anwenden Berechnen geometrische Größen und verwenden den Satz des Pythagoras Konstruieren Vergrößern und Verkleinern einfache Figuren maßstabsgetreu Anwenden Berechnen geometrische Größen und verwenden dazu Ähnlichkeitsbeziehungen Darstellen veranschaulichen zweistufige Zufalls experimente mithilfe von Diagrammen Konstruieren Analysieren grafische statistische Darstellungen kritisch und erkennen Manipulationen Argumentieren/ Kommunizieren *Verbalisieren mathematische Zusammenhänge *Überprüfen und bewerten Problembearbeitungen *Präsentieren eigene Ergebnisse in Vorträgen Problemlösen Zerlegen Probleme in Teilprobleme Vergleichen Lösungswege und bewerten sie Modellieren Übersetzen Realsituationen in mathematische Modelle Werkzeuge Argumentieren/ Kommunizieren Wählen ein geeignetes Werkzeug aus und nutzen es Erläutern mathematische Zusammenhänge und Einsichten mit eigenen Worten Präsentieren Problembearbeitungen in Vorträgen Modellieren Übersetzen Realsituationen in mathematische Modelle Werkzeuge Wählen ein geeignetes Werkzeug aus und nutzen es Nutzen Tabellenkalkulationsprogramme zum Erkunden Seite 3 von 3