Stoffplan
Werbung

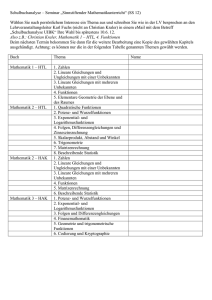
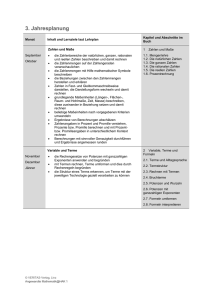
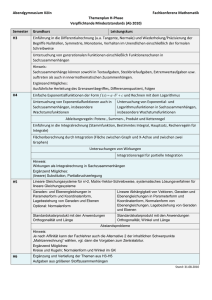
Mathematik Einführungsphase Sem. 1 2 BEGINN MIT DEM 1.SEMESTER (z.B. Vie-Dülken, Kempen) Die Zahlenbereiche N, Z, Q und Rechenregeln Termumformungen und lineare Gleichungen (binomische Formeln, Klammerregeln) Bruchrechnung Potenzen mit Exponenten aus Z Der Funktionsbegriff Lineare Funktionen Gleichungssysteme mit bis zu 3 Variablen Lineare Funktionen mit geometrischen Inhalten (Satz des Pythagoras, Einblick in trigonometrische Funktionen) Gleichungen höheren Grades quadratische Funktionen (Lösungsformel, Parabeln) Polynomdivision Reelle Zahlen R; Nichtlösbarkeit von x2 = 2 in der Menge Q Potenzen mit rationalen Exponenten, Wurzeln höherer Ordnung Exponentialfunktionen Exponentialgleichungen (Logarithmus) BEGINN MIT DEM 2.SEMESTER (z.B. Krefeld, Mönchengladbach) --- Voraussetzungen für eine erfolgreiche Teilnahme im 2.Semester: Bruchrechnung Termumformungen lineare Gleichungen 2 Potenzrechnung Der Funktionsbegriff lineare Funktionen, quadratische Funktionen, Gleichungen höheren Grades Polynomdivision lineare Gleichungssysteme (2 bis 3 Variablen) Allgemein: Grundbegriffe aus der Logik fließen überall dort ein, wo sich die Notwendigkeit ergibt und werden nicht als eigenständiges Thema behandelt. Falls ein Vorkurs stattfindet, können verstärkt geometrische Sachverhalte und auch Ungleichungen behandelt werden Kursphase Sem. GRUNDKURS 3/4 DIFFERENTIALRECHNUNG Ableitung von Funktionen Ableitungsregeln, Produkt- und Kettenregel Diskussion ganzrationaler Funktionen Diskussion von Exponentialfunktionen mit beliebiger Basis, Lösen von Exponentialgleichungen Anwendungen: Steckbriefaufgaben und einfache Extremwertaufgaben in Sachzusammenhängen komplexere Extremwertaufgaben INTEGRALRECHNUNG Integralfunktion Stammfunktion Hauptsatz Flächenberechnung Wirkungen Aufgaben in Sachzusammenhängen 5 6 LEISTUNGSKURS (zusätzliche Inhalte) exemplarische Beweise von Ableitungsregeln Quotientenregel gebrochen-rationale Funktionen (nur in Anwendungen) Logarithmusfunktionen ganz-rationale Kurvenscharen weitere Anwendungen der Differentialrechnung, zB Newton-Verfahren, Taylorpolynom-Entwicklung weitere Integrationsverfahren: Partielle Integration uneigentliche Integrale VEKTORRECHNUNG Grundoperationen mit Vektoren Systematisches Lösen von Gleichungssystemen Kollinearität und Komplanarität Parameterdarstellung von Geraden und Ebenen Ebenendarstellungen in Koordinatenform Lagebeziehungen von Geraden und Ebenen Skalarprodukt und Anwendungen: Längen- und Orthogonalität Winkelberechnungen Abstandsberechnungen Lineare Abhängigkeit Teilverhältnisse Normalenformen Abstandsberechnungen Vektorprodukt Kugeln (+ vertiefende Aufgaben aus der Integralrechnung) .................................................. oder STOCHASTIK als Alternative im 5.Sem. ................................................... Der Begriff der mathematischen Wahrscheinlichkeit mehrstufige Zufallsexperimente Grundtypen der Kombinatorik Wahrscheinlichkeitsverteilungen Erwartungswert, Standardabweichung Binomialverteilung, Bernoulliformel Testen von Hypothesen: einseitiger Signifikanztest Beweise zu Aussagen über Binomialkoeffizienten bedingte Wahrscheinlichkeit Tschebyscheff-Ungleichung Testen von Hypothesen: zweiseitiger Signifikanztest Binomialverteilung für große Werte von n und Näherungsformeln Normalverteilung ERGÄNZUNGEN UND VERTIEFUNGEN, INTEGRIERENDE WIEDERHOLUNG zB: Wachstumsmodelle zB Scharen von Exponentialfunktionen, zB einfache Differentialgleichungen