Unterrichtsinhalte
Werbung

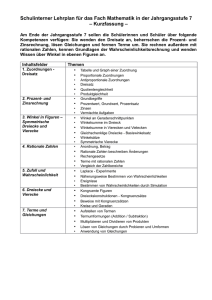
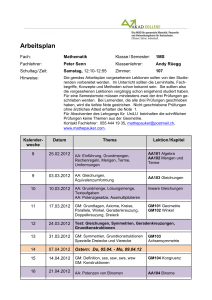
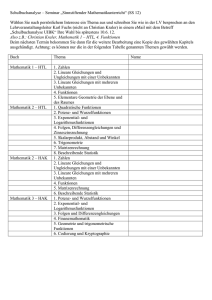
Unterrichtsinhalte im Fach Mathematik Jahrgang 5 Körper und Figuren Natürliche Zahlen Kreis – Winkel Bruchzahlen Flächen- und Rauminhalte Dezimalbrüche Brüche: Anteile und Verhältnisse Daten Jahrgang 6 Rechnen mir Bruchzahlen Zuordnungen – Dreisatz Prozent- und Zinsrechnung Symmetrie – Figuren und Abbildungen Zufall und Prognosen Rationale Zahlen Jahrgang 7 Dreiecke und Vierecke Terme und Gleichungen Berechnungen an Vielecken und Prismen Mehrstufige Zufallsexperimente Lineare Funktionen Jahrgang 8 Terme und Gleichungen mit Klammern Lineare Gleichungen mit zwei Variablen – Systeme linearer Gleichungen Quadratwurzeln – Reelle Zahlen Satz des Pythagoras Parabeln – Quadratische Funktionen und Gleichungen Jahrgang 9 Ähnlichkeit Trigonometrie Rückschlüsse aus Baumdiagrammen Potenzen - Exponentialfunktionen Figuren und Körper Jahrgang 10 Modellieren periodischer Vorgänge Wachstumsprozesse - Grenzwerte Differenzialrechnung Funktionsuntersuchungen Bemerkung: Die folgenden Inhalte gelten ab dem Schuljahr 2010/2011 für alle 11. Klassen und ab dem Schuljahr 2011/2012 für alle 12. Klassen. Im Schuljahr 2010/2011 gelten für den 12/13. Jahrgang (Q2) die alten Vorgaben inklusive der Schwerpunktthemen für die Abiturprüfung. Inhalte, die nur für Kurse auf erhöhtem Niveau gelten, sind mit * markiert und im Lehrbuch besonders hervorgehoben. Jahrgang 11/12 Analysis Kurvenanpassung – Lineare Gleichungssysteme Krümmung, Wendepunkte, Bestimmen ganzrationaler Funktionen, Lösen von LGS, Gauss-Algorithmus, Anpassung von Funktionen, Stetigkeit, Differenzierbarkeit, Funktionenscharen Integralrechnung Begriff des Integrals, Intergralfunktion, Hauptsatz DIR, Integration mittels Stammfunktionen, Berechnen von Flächeninhalten, *Volumina von Rotationskörpern Wachstumsmodelle Exponentielles Wachstum, e-Funktion, Natürlicher Logarithmus, *DGL, Begrenztes Wachstum, Logistisches Wachstum, Ableitungsregeln, Funktionsuntersuchungen Analytische Geometrie Punkte und Vektoren im Raum, Geraden im Raum, Lage Gerade – Gerade, Winkel im Raum, Ebenen im Raum, Lage Gerade – Ebene, *Lagebeziehungen zwischen Ebenen Matrizen Addition und Vervielfachen, Multiplikation, Materialverflechtung, Inverse Matrix, Bedarfsermittlung, Zustandsänderungen, *Populationsentwicklung Stochastik Häufigkeitsverteilungen – Beschreibende Statistik Merkmale, Relative Häufigkeit, Histogramme, Streuung, Empirische Standardabweichung Wahrscheinlichkeitsverteilung Zufallsgröße, Erwartungswert, Binomialverteilung, Bernoulli-Ketten, Erwartungswert, Anwendungen der Binomialverteilung Beurteilende Statistik Binomialverteilung für große Stufenzahlen, Sigma-Regeln, Schluss von der Gesamtheit auf die Stichprobe, Schluss von der Stichprobe auf die Gesamtheit, Konfidenzintervalle, *Normalverteilung, *Stetige Zufallsgrößen