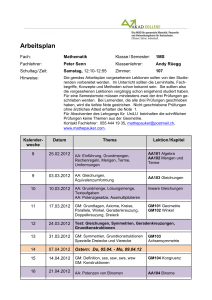
Beweis der Repräsentantenunabhängigkeit der Multiplikation

Beweis der Repräsentantenunabhängigkeit der Addition
Voraussetzung:
( x1 , x2 ) ( x1 ', x2 ') 
I
x1  x2 '  x2  x1 '
( y1 ', y2 ') 
( y1 , y2 )
II
y1  y2 '  y2  y1 '
Zu zeigen:
[( x1, x2 )]  [( y1, y2 )]  [( x1 ', x2 ')]  [( y1 ', y2 ')]
Verknüpft man die symbolischen Darstellungen zweier ganzer Zahlen x und y entsprechend
der Definition, so erhält man wieder die symbolische Darstellung einer ganzen Zahl. Eine
Verknüpfung in der Menge der ganzen Zahlen liegt aber erst dann vor, wenn die Verknüpfung
bei äquivalenten Repräsentanten stets zur selben Zahl führt.......
[( x1 , x2 )]  [( y1 , y2 )]  [( x1 ', x2 ')]  [( y1 ', y2 ')] 
[( x1  y1 , x2  y2 )]  [( x1 ' y1 ', x2 ' y2 ')] 
( x1  y1 , x2  y2 )
( x1 ' y1 ', x2 ' y2 ') 
x1  y1  x2 ' y2 '  x2  y2  x1 ' y1 ' (I+II)
q.e.d.
Beweis der Repräsentantenunabhängigkeit der Multiplikation
Voraussetzung:
( x1 , x2 ) ( x1 ', x2 ') 
( y1 , y2 )
( y1 ', y2 ') 
I
x1  x2 '  x2  x1 ' 
II
y1  y2 '  y2  y1 ' 
I
x2  x1 '  x1  x2 '
II
y2  y1 '  y1  y2 '
Zu zeigen:
[( x1 , x2 )]  [( y1 , y2 )]  [( x1 ', x2 ')]  [( y1 ', y2 ')] 
[( x1 y1  x2 y2 , x1 y2  x2 y1 )]  [( x1 ' y1 ' x2 ' y2 ', x1 ' y2 ' x2 ' y1 ')] 
( x1 y1  x2 y2 , x1 y2  x2 y1 )
( x1 ' y1 ' x2 ' y2 ', x1 ' y2 ' x2 ' y1 ') 
x1 y1  x2 y2  x1 ' y2 ' x2 ' y1 '  x1 y2  x2 y1  x1 ' y1 ' x2 ' y2 ' (*)
Die Gültigkeit der Gleichung * ist hier nicht so leicht aus den Gleichungen I und II der
Voraussetzung ableitbar. Zunächst bietet es sich schon aus Gründen der Analogie an,
einen Versuch mit III zu machen. Es zeigt sich aber dass auch das Vertauschen von
linker und rechter Seite nicht zu passenden Produktpaaren führt. Der Versuch
systematisch die Gleichungen I und II (bzw. I und II ) so mit geeigneten Variablen zu
multiplizieren, sodass die benötigten Paare erzeugt werden, und schließlich
aufzusummieren führt hingegen zum Ziel. Die dabei zusätzlich entstandenen Terme
(hier in grauer Farbe markiert) heben sich gegenseitig weg.
I  y1 : x1y1  x2 ' y1  x2 y1  x1 ' y1
I  y 2 : x2 y 2  x1 ' y 2  x1y 2  x2 ' y 2
x1 ' II: x1 ' y1  x1 ' y2 '  x1 ' y2  x1 ' y1 '
x2 ' II: x2 ' y2  x2 ' y1 '  x2 ' y1  x2 ' y2 '

x1 y1  x2 y2  x1 ' y2 ' x2 ' y1 '  x1 y2  x2 y1  x1 ' y1 ' x2 ' y2 '
q.e.d.