Lösung - HS Vossbarg

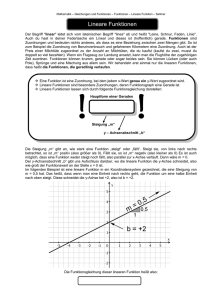
Mathematik – Gleichungen und Funktionen – Funktionen – Lineare Funktion – Sellmer
Lineare Funktionen
Der Begriff "linear" leitet sich vom lateinischen Begriff "linea" ab und heißt "Leine, Schnur, Faden, Linie".
Auch du hast in deiner Federtasche ein Lineal und dieses ist (hoffentlich) gerade. Funktionen sind
Zuordnungen und bedeuten nichts anderes, als dass es eine Beziehung zwischen zwei Mengen gibt. So ist
zum Beispiel die Zuordnung von Benzinverbrauch und gefahrenen Kilometern eine Zuordnung. Auch ist der
Preis einer Milchtüte zugeordnet zu der Anzahl an Milchtüten, die du kaufst (kaufst du zwei, musst du
doppelt so viel bezahlen). Wenn ein Flugzeug zur Landung ansetzt, kann man die Flughöhe der zugehörigen
Zeit zuordnen. Funktionen können krumm, gerade oder sogar beides sein. Sie können Lücken (oder auch
Pole), Sprünge und eine Mischung aus allem sein. Wir behandeln erst einmal nur die linearen Funktionen,
dass heißt die Funktionen, die geradlinig verlaufen.
 Eine Funktion ist eine Zuordnung, bei dem jedem x-Wert genau ein y-Wert zugeordnet wird.
 Lineare Funktionen sind besondere Zuordnungen, deren Funktionsgraph eine Gerade ist.
 Lineare Funktionen lassen sich durch folgende Funktionsgleichung darstellen:
Hauptform einer Geraden
y = m•x + b
Steigung „m“
y – Achsenabschnitt „b“
Die Steigung „m“ gibt an, wie stark eine Funktion „steigt“ oder „fällt“. Steigt sie, von links nach rechts
betrachtet, so ist „m“ positiv (also größer als 0). Fällt sie, so ist „m“ negativ (also kleiner als 0) Es ist auch
möglich, dass eine Funktion weder steigt noch fällt, also parallel zur x-Achse verläuft. Dann wäre m = 0.
Der y-Achsenabschnitt „b“ gibt uns Aufschluss darüber, wo die lineare Funktion die y-Achse schneidet, also
wie groß der Funktionswert an der Stelle x = 0 ist.
Im folgenden Beispiel ist eine lineare Funktion in ein Koordinatensystem gezeichnet, die eine Steigung von
m = 0,5 hat. Das heißt, dass wenn man eine Einheit nach rechts geht, die Funktion um eine halbe Einheit
nach oben steigt. Diese schneidet die y-Achse bei +2, also ist b = +2.
Die Funktionsgleichung dieser linearen Funktion heißt also:
y = 0,5 • x + 2