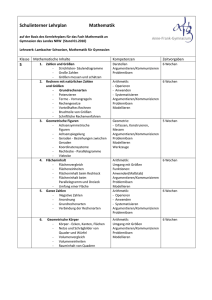
5 - Abtei-Gymnasium Brauweiler
Werbung
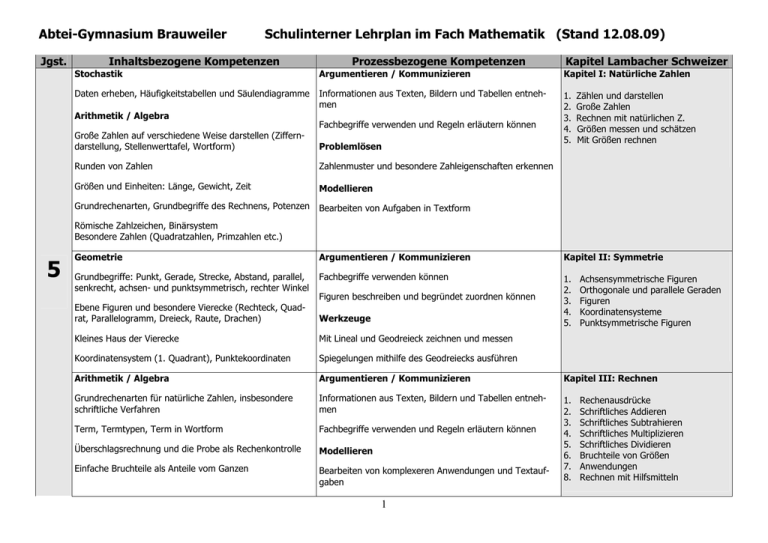
Abtei-Gymnasium Brauweiler Jgst. Schulinterner Lehrplan im Fach Mathematik (Stand 12.08.09) Inhaltsbezogene Kompetenzen Prozessbezogene Kompetenzen Kapitel Lambacher Schweizer Stochastik Argumentieren / Kommunizieren Kapitel I: Natürliche Zahlen Daten erheben, Häufigkeitstabellen und Säulendiagramme Informationen aus Texten, Bildern und Tabellen entnehmen 1. 2. 3. 4. 5. Arithmetik / Algebra Fachbegriffe verwenden und Regeln erläutern können Große Zahlen auf verschiedene Weise darstellen (Zifferndarstellung, Stellenwerttafel, Wortform) Problemlösen Runden von Zahlen Zahlenmuster und besondere Zahleigenschaften erkennen Größen und Einheiten: Länge, Gewicht, Zeit Modellieren Grundrechenarten, Grundbegriffe des Rechnens, Potenzen Bearbeiten von Aufgaben in Textform Zählen und darstellen Große Zahlen Rechnen mit natürlichen Z. Größen messen und schätzen Mit Größen rechnen Römische Zahlzeichen, Binärsystem Besondere Zahlen (Quadratzahlen, Primzahlen etc.) 5 Geometrie Argumentieren / Kommunizieren Kapitel II: Symmetrie Grundbegriffe: Punkt, Gerade, Strecke, Abstand, parallel, senkrecht, achsen- und punktsymmetrisch, rechter Winkel Fachbegriffe verwenden können 1. 2. 3. 4. 5. Figuren beschreiben und begründet zuordnen können Achsensymmetrische Figuren Orthogonale und parallele Geraden Figuren Koordinatensysteme Punktsymmetrische Figuren Ebene Figuren und besondere Vierecke (Rechteck, Quadrat, Parallelogramm, Dreieck, Raute, Drachen) Werkzeuge Kleines Haus der Vierecke Mit Lineal und Geodreieck zeichnen und messen Koordinatensystem (1. Quadrant), Punktekoordinaten Spiegelungen mithilfe des Geodreiecks ausführen Arithmetik / Algebra Argumentieren / Kommunizieren Kapitel III: Rechnen Grundrechenarten für natürliche Zahlen, insbesondere schriftliche Verfahren Informationen aus Texten, Bildern und Tabellen entnehmen Term, Termtypen, Term in Wortform Fachbegriffe verwenden und Regeln erläutern können Überschlagsrechnung und die Probe als Rechenkontrolle Modellieren Einfache Bruchteile als Anteile vom Ganzen Bearbeiten von komplexeren Anwendungen und Textaufgaben 1. 2. 3. 4. 5. 6. 7. 8. 1 Rechenausdrücke Schriftliches Addieren Schriftliches Subtrahieren Schriftliches Multiplizieren Schriftliches Dividieren Bruchteile von Größen Anwendungen Rechnen mit Hilfsmitteln Geometrie Problemlösen Umfänge von Vielecken und ebenen Figuren durch Messen Sinnvolle Einteilung von ebenen Figuren zur Berechnung bestimmen, Flächeninhalte von Rechtecken und ebenen von Umfängen und Flächeninhalten Figuren durch Auszählen von Einheitsquadraten bestimmen Arithmetik / Algebra Flächeneinheiten umrechnen Kapitel IV: Flächen 1. 2. 3. 4. 5. Welche Figur ist größer Flächeneinheiten Flächeninhalt eines Rechtecks Flächeninhalte veranschaulichen Flächeninhalt eines Parallelogramms und eines Dreiecks 6. Umfang einer Fläche Flächeninhalt des Rechtecks, des Dreiecks und des Parallelogramms berechnen, Höhen Umfang von Vielecken berechnen 5 Geometrie Werkzeuge Kapitel V: Körper Grundfiguren und Grundkörper: Quader, Würfel, Prisma, Kegel, Zylinder, Pyramide Herstellen von verschiedenen Körpern 1. 2. 3. 4. 5. Netz des Würfels, des Quaders und anderer Körper Schrägbilder des Quaders und anderer Körper Arithmetik / Algebra Volumeneinheiten umrechnen Volumen und Oberfläche des Quaders berechnen 2 Körper und Netze Quader Schrägbilder Messen von Rauminhalten Rauminhalt von Quadern Arithmetik / Algebra Argumentieren / Kommunizieren Kapitel VI: Ganze Zahlen Erweiterung des Zahlenstrahls zur Zahlengerade Informationen aus Texten, Bildern und Tabellen entnehmen Fachbegriffe verwenden und Regeln erläutern können 1. 2. 3. 4. Problemlösen 5. Grundbegriffe: negative und positive Zahlen, ganze Zahlen Anordnung der ganzen Zahlen Grundrechenarten mit ganzen Zahlen ausführen Besondere Zahleigenschaften erkennen Kombination von Rechenarten, Rechenregel, u.a. Klammerregeln Modellieren 6 6. Negative Zahlen Anordnung Zunahme und Abnahme Addieren und Subtrahieren einer positiven Zahl Addieren und Subtrahieren einer negativen Zahl Verbinden von Addition und Subtraktion Multiplizieren von ganzen Z. Dividieren von ganzen Zahlen Verbinden der Rechenarten Koordinatensystem mit vier Quadranten Bearbeiten von Aufgaben in Textform 7. 8. 9. Arithmetik / Algebra Argumentieren / Kommunizieren Kapitel I: Rationale Zahlen Teilbarkeit, kgV und ggT, Primfaktorzerlegung Fachbegriffe verwenden und Regeln erläutern können Kürzen und erweitern von Brüchen Problemlösen Dezimalbrüche, Prozentschreibweise Besondere Zahleigenschaften erkennen Anordnung von Brüchen und Dezimalbrüchen Modellieren 1. Brüche und Anteile 2. Was man mit einem Bruch alles machen kann 3. Kürzen und Erweitern 4. Die drei Gesichter einer rationalen Zahl 5. Ordnung in die Brüche bringen 6. Dezimalschreibweise bei Größen Graphische Darstellung von Brüchen und Anteilen Arithmetik / Algebra Argumentieren / Kommunizieren Addieren und Subtrahieren von Brüchen und Dezimalbrüchen Informationen aus Texten, Bildern und Tabellen entnehmen Runden von Dezimalbrüchen Fachbegriffe verwenden und Regeln erläutern können Rechenregeln, Assoziativ- und Kommutativgesetz, Rechen- Modellieren vorteile Bearbeiten von Aufgaben in Textform 3 Kapitel II: Addition und Subtraktion von rationalen Zahlen 1. Addieren und Subtrahieren von Brüchen 2. Addieren und Subtrahieren von Dezimalzahlen 3. Runden und Überschlagen bei Dezimalzahlen 4. Geschicktes Rechnen Geometrie Argumentieren / Kommunizieren Kapitel III: Winkel und Kreis Winkel, Winkelbegriffe, Grad als Winkelmaß, Winkelarten Fachbegriffe verwenden Winkel messen und zeichnen Modellieren Kreise, Kreisausschnitte, Mittelpunktswinkel Geographische Karten, Kompass und Himmelsrichtungen mithilfe von Winkeln mathematisieren 1. Winkel 2. Winkel schätzen, messen und zeichnen 3. Kreisfiguren Orientierung im Gelände, Winkel und Himmelsrichtungen, Positionsbestimmung Werkzeuge Umgang mit dem Geo-Dreieck und Zirkel Arithmetik / Algebra Argumentieren / Kommunizieren Multiplikation und Division von Brüchen und Dezimalbrüchen Informationen aus Texten, Bildern und Tabellen entnehmen Zehnerpotenzen, Maßstäbe Fachbegriffe verwenden und Regeln erläutern können Rechenterme und Rechengesetze, Distributivgesetz Problemlösen Abbrechende und periodische Dezimalbrüche Besondere Zahleigenschaften erkennen Modellieren Bearbeiten von Aufgaben in Textform 6 Stochastik Argumentieren / Kommunizieren Relative und absolute Häufigkeiten Informationen aus Texten, Bildern und Tabellen entnehmen Säulen-, Streifen- und Kreisdiagramme erstellen Mittelwerte (arithmetisches Mittel, Median) Boxplots, Quartil, Quartilabstand Statistische Maße und Daten erläutern und einordnen Werkzeuge Einführung in Excel (möglich) 4 Kapitel V: Multiplikation und Division von rationalen Zahlen 1. Vervielfachen und Teilen von Brüchen 2. Multiplizieren von Brüchen 3. Dividieren von Brüchen 4. Multiplizieren u. Dividieren von Zehnerpotenzen - Maßstäbe 5. Multiplizieren von Dezimalzahlen 6. Dividieren einer Dezimalzahlen 7. Grundregeln für Rechenausdrücke – Terme 8. Rechengesetze – Vorteile beim Rechnen Kapitel VI: Daten erfassen, darstellen und interpretieren 1. Relative Häufigkeiten und Diagramme 2. Mittelwerte 3. Boxplots Arithmetik / Algebra Argumentieren / Kommunizieren Zahlenfolgen, einfache Terme mit einer Variablen, rekursive Formel, Fibonacci-Zahlen Mathematische Sachverhalte und Verfahren erläutern Funktionen Beziehungen zwischen Tabellen und Diagrammen Punkt- und Liniendiagramme Geometrie Mathematisch begründen, Plausibilitätsüberlegungen Problemlösen Kapitel VII: Muster und Abhängigkeiten 1. Muster erkunden 2. Von Mustern und Termen 3. Muster darstellen Problemlösestrategien „Beispiele finden“, „Überprüfen durch Probieren“ anwenden Ergebnisse in Bezug auf die ursprüngliche Problemstellung deuten Geometrische Muster, Verschiebungen, Symmetrien 7 Funktionen Modellieren Kapitel III: Zuordnungen Qualitative Analyse von Graphen Realsituationen in mathematische Modelle übersetzen Zuordnungen, Wertetabelle, Proportionale und antiproportionale Zuordnungen, Dreisatz Mathematische Modelle überprüfen und ggf. das Modell verändern Lineare Zuordnungen Einem mathematischen Modell (Tabelle, Graph) eine passende Realsituation zuordnen 1. 2. 3. 4. 5. 5 Zuordnungen und Graphen Gesetzmäßigkeiten bei Zuordnungen Proportionale Zuordnungen Antiproportionale Zuordnungen Lineare Zuordnungen Arithmetik / Algebra Argumentieren / Kommunizieren Kapitel I: Prozente und Zinsen Vergleichen mit Prozentangaben Informationen aus Texten, Bildern und Tabellen entnehmen 1. Prozente – Vergleiche werden einfacher 2. Prozentsatz – Prozentwert – Grundwert 3. Grundaufgaben der Prozentrechnung 4. Zinsen 5. Zinseszinsen 6. Überall Prozente Funktionen Fachbegriffe verwenden und Regeln erläutern können Grundbegriffe und Grundaufgaben der Prozentrechnung Problemlösen Steigungsprozente Mehrere Lösungswege bei Problemen finden Zinsrechnung, Jahreszinsen, Monats- und Tageszinsen Modellieren Einfache Realsituationen in mathematische Modelle übersetzen Werkzeuge Einführung des Taschenrechners Einführung in Excel (spätestens hier) Stochastik Argumentieren / Kommunizieren Statistische Wahrscheinlichkeit, Zufallsexperimente Lösungswege, Argumentationen und Darstellungen vergleichen und bewerten. Laplace-Wahrscheinlichkeit, Summenregel Simulation und Schätzwerte 6 Kapitel II: Relative Häufigkeiten und Wahrscheinlichkeiten 1. Wahrscheinlichkeiten 2. Laplace-Wahrscheinlichkeiten, Summenregel 3. Simulation, Zufallsschwankungen Arithmetik / Algebra Terme mit einer Variablen, Terme umformen und vereinfachen, Distributivgesetz Lineare Gleichungen, Äquivalenzumformungen Argumentieren / Kommunizieren Kapitel IV: Terme und Gleichungen Fachbegriffe verwenden und Regeln erläutern können Realsituationen in mathematische Modelle übersetzen 1. Mit Termen Probleme lösen 2. Gleichwertige Terme – Umformen mit Rechengesetze 3. Ausmultiplizieren und Ausklammern – Distributivgesetz 4. Gleichungen umformen – Äquivalenzumformungen 5. Lösen von Problemen mit Strategien Argumentieren / Kommunizieren Kapitel V: Beziehungen in Dreiecken Modellieren Anwendung von linearen Gleichungen Geometrie Dreieckskonstruktionen, Kongruenz, Kongruenzsätze Dreiecksarten, gleichschenklige Dreiecke, Basiswinkelsatz 7 Arbeitsschritte mit eigenen Worten und geeigneten Fachbegriffen erläutern (Konstruktionen) Mittelsenkrechte, Winkelhalbierende, Umkreis, Inkreis, Satz Werkzeuge des Thales, Kreistangenten Konstruktion mit Lineal und Zirkel und mithilfe einer Geometriesoftware Seitenhalbierende, Schwerpunkt Winkelbeziehungen, Winkelsummensätze Problemlösen Muster und Beziehungen bei Figuren untersuchen und Vermutungen aufstellen 7 1. Dreiecke konstruieren 2. Kongruente Dreiecke 3. Mittelsenkrechte und Winkelhalbierende 4. Umkreise und Inkreise 5. Winkelbeziehungen erkunden 6. Regeln für Winkelsummen entdecken 7. Der Satz des Thales Arithmetik / Algebra Argumentieren / Kommunizieren Lineare Gleichungen mit zwei Variablen Fachbegriffe verwenden und Regeln erläutern können Einsetzungs-, Gleichsetzungs- und Additionsverfahren Modellieren Funktionen Realsituationen in mathematische Modelle übersetzen Lineare Gleichungssysteme graphisch lösen 8 Kapitel VI: Systeme linearer Gleichungen 1. Lineare Gleichungen mit zwei Variablen 2. Lineare Gleichungssysteme – grafisches Lösen 3. Lineare Gleichungssysteme – rechnerische Lösen 4. Lineare Gleichungssysteme – Additionsverfahren Arithmetik / Algebra Argumentieren / Kommunizieren Kapitel I: Reelle Zahlen Irrationale Zahlen, reelle Zahlen Fachbegriffe verwenden und Regeln erläutern können Quadratwurzeln, höhere Wurzeln Problemlösen Wurzelterme, Rechenregeln bei Wurzeln Besondere Zahleigenschaften erkennen 1. Von bekannten und neuen Zahlen 2. Wurzeln und Streckenlängen 3. Der geschickte Umgang mit Wurzeln - Wurzelterme 4. Rechnen im Kontext – der Umgang mit Näherungswerten Arithmetik / Algebra Argumentieren / Kommunizieren Algebraische Umformungen, binomische Formeln Fachbegriffe verwenden und Regeln erläutern können Formeln nach einer Variablen umformen Modellieren Geometrie Realsituationen in mathematische Modelle übersetzen Eigenschaften von besonderen Vierecken (Haus der Vierecke) Flächeninhalt des Trapez, Flächeninhalt von Vielecken Kreisumfang und –fläche, Kreisbogen, Kreisausschnitt Volumen und Oberfläche von Prismen und Zylinder 8 Kapitel II: Flächen und Volumina – vom Umgang mit Formeln 1. Formeln aufstellen, vereinfachen und auflösen 2. Zusammengesetzte Flächen – binomische Formeln 3. Flächeninhalt von Dreiecken, Parallelogrammen u. Trapezen 4. Flächeninhalt von Vielecken 5. Kreise 6. Kreisteile 7. Prisma und Zylinder Stochastik Argumentieren / Kommunizieren Zufallsversuche, Ergebnis, Ereignis, Gegenereignis Fachbegriffe verwenden und Regeln erläutern können Baumdiagramm, Pfadregel, Summenregel Lösungswege, Argumentationen und Darstellungen vergleichen und bewerten Urnenmodell, Ziehen mit und ohne Zurücklegen Modellieren Kapitel III: Wahrscheinlichkeitsrechnung 1. Pfadregel, Wahrscheinlichkeitsverteilung 2. Der richtige Blick aufs Diagramm 3. Pascalsches Dreieck und Wahrscheinlichkeiten Realsituationen in mathematische Modelle übersetzen Mathematische Modelle überprüfen und ggf. das Modell verändern 8 Funktionen Modellieren Lineare Funktionen, Steigungsdreieck, Funktionsgleichungen aufstellen Realsituationen in mathematische Modelle übersetzen Quadratische Funktionen, Parabel, Verschobene Parabeln, Scheitelpunktform Parabelgleichungen bestimmen (Gleichungssysteme) Kapitel IV: Lineare und quadratische Funktionen 1. Lineare Funktionen 2. Aufstellen von linearen Funktionsgleichungen 3. Quadratische Funktionen y = ax² Problemlösen 4. Quadratische Funktionen Ergebnisse in Bezug auf die ursprüngliche Problemstellung 5. Aufstellen von quadratischen Funktionsgleichungen deuten 6. Mit Funktionen die Wirklichkeit beschreiben – Modellieren Werkzeuge Mathematische Modelle überprüfen und ggf. das Modell verändern Funktionsgraphen mit Derive zeichnen 9 Arithmetik / Algebra Modellieren Lösen quadratischer Gleichungen (Quadratische Ergänzung, pq-Formel, Satz von Vieta) Realsituationen in mathematische Modelle übersetzen Anwendung quadratischer Funktionen zur Lösung von Extremwertproblemen 1. Wiederholen – Aufstellen von Funktionsgleichungen 2. Scheitelpunktbestimmung – quadratische Ergänzung Problemlösen 3. Lösen einfacher quadratischer Gleichungen Ergebnisse in Bezug auf die ursprüngliche Problemstellung 4. Lösen allgemeiner quadratischer Gleideuten chungen 5. Lösen quadratischer Gleichungen mit Werkzeuge der pq-Formel 6. Probleme lösen Funktionsgraphen mit Derive zeichnen Geometrie Argumentieren / Kommunizieren Ähnliche Figuren, Ähnlichkeitsfaktor, Seitenverhältnisse Mathematische Sachverhalte und Verfahren erläutern und begründen Funktionen Parabel, Normalparabel, verschobene Parabeln, Parabelgleichungen, Scheitelpunktform Modellieren mithilfe von Parabeln (Bsp.: Brücken, Wurfparabel) 9 Eigenschaften ähnlicher Dreiecke, Strahlensätze Maßstabsgetreue Vergrößerung und Verkleinerung von Figuren (zentrische Streckung) 9 Kapitel I: Quadratische Funktionen und quadratische Gleichungen Mathematische Modelle überprüfen und ggf. das Modell verändern Problemlösen Zerlegen von Problemen in Teilprobleme Geometrie Argumentieren / Kommunizieren Rechtwinklige Dreiecke (Begriffe), Satz des Pythagoras Mathematische Sachverhalte und Verfahren erläutern und begründen Katheten- und Höhensatz, Berechnung geometrischer Größen unter Verwendung des Satzes von Pythagoras Problemlösen Oberfläche und Volumen von Pyramide und Kegel, Kugelvolumen und -oberfläche Zerlegen von Problemen in Teilprobleme Kugelabschnitt, Ring, Kegel- und Pyramidenstumpf 10 Kapitel II: Ähnliche Figuren Strahlensätze 1. Vergrößern und Verkleinern von Figuren – Ähnlichkeit 2. Zentrische Streckung 3. Ähnliche Dreiecke 4. Strahlensätze Kapitel III: Formeln in Figuren und Körpern 1. 2. 3. 4. Der Satz des Pythagoras Katheten- und Höhensatz Pythagoras in Figuren und Körpern Formeln verstehen: Pyramiden und Kegel 5. Formeln anwenden: Kugeln und andere Körper 6. Vorwärts- und Rückwärtsarbeiten Arithmetik / Algebra Argumentieren / Kommunizieren Kapitel IV: Potenzen Zehnerpotenzen, wissenschaftliche Schreibweise Fachbegriffe verwenden und Regeln erläutern können Potenzgesetze Werkzeuge Einfache Exponentialgleichungen, Logarithmus Große und sehr kleine Zahlen mit dem Taschenrechner schreiben, Verwenden der Logarithmus-Taste 1. Zehnerpotenzen 2. Der geschickte Umgang mit Potenzen – Potenzgesetze 3. Einfache Gleichungen mit Potenzen – Basis gesucht 4. Einfache Gleichungen mit Potenzen – Exponent gesucht Arithmetik / Algebra Argumentieren / Kommunizieren Kapitel V: Wachstumsvorgänge Lineares und exponentielles Wachstum, Zinsrechnung Mathematische Sachverhalte und Verfahren erläutern und begründen 1. Exponentielles Wachstum 2. Zinseszins und andere Wertentwicklungen untersuchen 3. Rechnen mit exponentiell. Wachstum Funktionen Werkzeuge Modellieren von exponentiellen Wachstums- und Zerfallsprozessen mithilfe von Exponentialfunktionen Zinsrechnung mit Excel Geometrie Argumentieren / Kommunizieren Sinus, Kosinus, Tangens, Berechnungen an rechtwinkligen und beliebigen Dreiecken Mathematische Sachverhalte und Verfahren erläutern und begründen Sinus und Kosinus am Einheitskreis, Grad- und Bogenmaß Modellieren Funktionen Realsituationen in mathematische Modelle übersetzen Sinusfunktion, Amplitude und Periode, Modellieren von periodischen Vorgängen mithilfe von Sinusfunktionen 11 Kapitel VI: Trigonometrie – Berechnungen an Dreiecken und periodischen Vorgängen 1. Sinus und Kosinus 2. Tangens 3. Probleme lösen im rechtwinkligen Dreieck 4. Die Sinusfunktion 5. Amplitude und Periode von Sinusfunktionen 6. Beschreibung periodischer Vorgänge