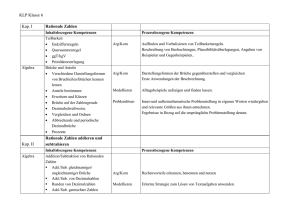
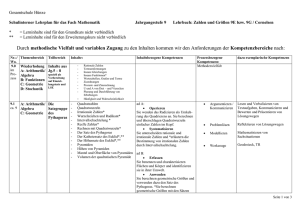
Prozessbezogene Kompetenzen

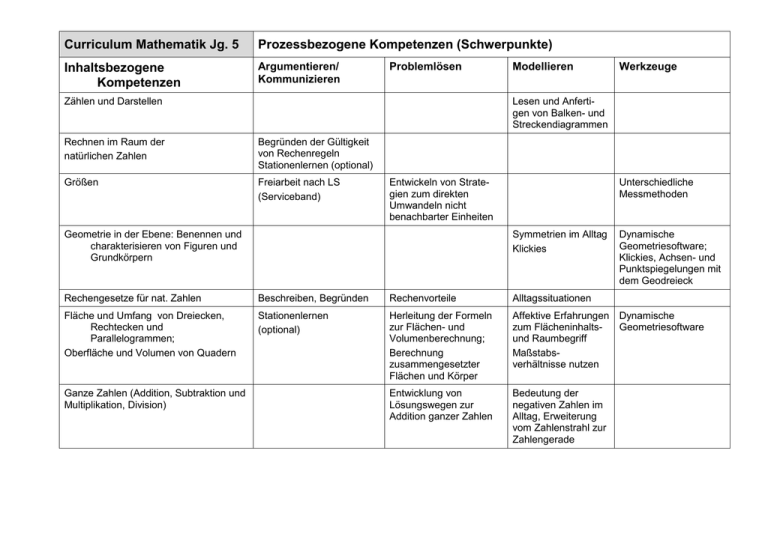
Curriculum Mathematik Jg. 5
Prozessbezogene Kompetenzen (Schwerpunkte)
Inhaltsbezogene
Kompetenzen
Argumentieren/
Kommunizieren
Problemlösen
Zählen und Darstellen
Modellieren
Lesen und Anfertigen von Balken- und
Streckendiagrammen
Rechnen im Raum der
natürlichen Zahlen
Begründen der Gültigkeit
von Rechenregeln
Stationenlernen (optional)
Größen
Freiarbeit nach LS
(Serviceband)
Entwickeln von Strategien zum direkten
Umwandeln nicht
benachbarter Einheiten
Geometrie in der Ebene: Benennen und
charakterisieren von Figuren und
Grundkörpern
Unterschiedliche
Messmethoden
Symmetrien im Alltag
Klickies
Rechengesetze für nat. Zahlen
Beschreiben, Begründen
Rechenvorteile
Alltagssituationen
Fläche und Umfang von Dreiecken,
Rechtecken und
Parallelogrammen;
Oberfläche und Volumen von Quadern
Stationenlernen
(optional)
Herleitung der Formeln
zur Flächen- und
Volumenberechnung;
Berechnung
zusammengesetzter
Flächen und Körper
Affektive Erfahrungen
zum Flächeninhaltsund Raumbegriff
Maßstabsverhältnisse nutzen
Entwicklung von
Lösungswegen zur
Addition ganzer Zahlen
Bedeutung der
negativen Zahlen im
Alltag, Erweiterung
vom Zahlenstrahl zur
Zahlengerade
Ganze Zahlen (Addition, Subtraktion und
Multiplikation, Division)
Werkzeuge
Dynamische
Geometriesoftware;
Klickies, Achsen- und
Punktspiegelungen mit
dem Geodreieck
Dynamische
Geometriesoftware
Curriculum Mathematik Jg. 6
Prozessbezogene Kompetenzen (Schwerpunkte)
Inhaltsbezogene
Kompetenzen
Argumentieren/
Kommunizieren
Modellieren
Werkzeuge
Erfassen und
Systematisieren von
Teilbarkeitsregeln
Teiler und Vielfache (ggT; kgV)
Bruchrechnung
Vernetzen von
unterschiedlichen
Schreibweisen
(Dezimalbruch ↔
gemischte/unechte
Brüche)
Dezimalbrüche
Stationenlernen oder
Stationenüben als
Sicherung (optional)
Rechengesetze
Gültigkeit der Gesetze
begründen
Winkel und Kreis
Zeichnen von
überstumpfen Winkeln
Strategien entwickeln,
Problemlösen
Lösungsstrategien
darstellen und begründen
Muster und Abhängigkeiten
Mittelwerte, relative
Häufigkeiten, Boxplots
Problemlösen
Entdeckung von
Rechenregeln
Verschiedene
Darstellungen von
Anteilen
Alltagssituationen
mathematisch
modellieren.
Dynamische
Geometriesoftware,
Konstruktionen mit
Geodreieck und
Zirkel
Erkunden Muster in
Beziehungen
zwischen Zahlen
Erfassen und Präsentieren
statistischer Erhebungen
Anfertigen von
Kreisdiagrammen
Tabellenkalkulation
Curriculum Mathematik Jg. 7
Prozessbezogene Kompetenzen (Schwerpunkte)
Inhaltsbezogene Kompetenzen
Argumentieren/
Kommunizieren
Winkel an Geradenkreuzungen,
Winkelsumme in Vielecken
Mehrschrittiges Begründen
Symmetriebetrachtungen
Kongruenzsätze für Dreiecke
Konstruktionsbeschreibungen
Besondere Linien im Dreieck,
Umkreis / Inkreis
Präsentieren und
Begründen von
Konstruktionen
Zuordnungen und Dreisatz
(proportional, antiproportional, lineare)
Stationenlernen in der
Gruppe
Problemlösen
Entwickeln von
Strategien zum
Konstruieren von
Dreiecken
Vor- und Nachteile
verschiedener
Lösungsverfahren
Wahrscheinlichkeiten, Laplace-Regel,
Pfadregel, Simulationen
(relative Häufigkeit, Boxplots optional als
Wiederholung)
(Präsentieren und
Interpretieren von
Ergebnissen eigener
Datenerfassungen)
Konstruktionen mit
Zirkel und Lineal,
dynamische
Geometriesoftware
Dynamische
Geometriesoftware
Anwenden des
Dreisatzes in innerund außermathematischen
Problemstellungen
(geschicktes)
Anwenden der
Regeln für Term- und
Äquivalenzumformung
Lineare Gleichungssysteme
Werkzeuge
Dynamische
Geometriesoftware
Prozentrechnung, Zinsrechnung
Terme und Gleichungen
Modellieren
Anfertigen von
Diagrammen anhand
praktischer Beispiele
Zuordnungen von
realen Situationen zu
mathematischen
Darstellungen
Tabellenkalkulation,
Einführung
Taschenrechner
Prozente im Alltag
Taschenrechner
Internetrecherche
Aufstellen von
Gleichungen zur
Lösung inner- und
außermathematischer
Probleme
Nutzen verschiedener Algorithmen,
graphisches
Lösungsverfahren
einschl. Proben
GTR
Wahrscheinlichkeit im
Alltag,
Zufallsexperimente
Tabellenkalkulation/
GTR
Curriculum Mathematik Jg. 8
Prozessbezogene Kompetenzen (Schwerpunkte)
Inhaltsbezogene Kompetenzen
Argumentieren/
Kommunizieren
Reelle Zahlen, Wurzeln
Führen von Beweisen
Problemlösen
Modellieren
Rechnen mit
Näherungswerten
Flächen- und Rauminhalte (Trapeze,
Dreiecke, Prismen, Zylinder)
Herleitung der
Formeln zur Flächenund
Volumenberechnung
Binomische Formeln
Bin. Formeln als
Rechenstrategie
Kreise (Umfang und Flächeninhalt,
Kreisfiguren)
Erkennen von Kreisen
und Kreissegmenten
in komplexen Figuren
zur
Flächeninhaltsberech
nung (in der Umwelt)
Wahrscheinlichkeiten, Pfadregel,
Baumdiagramme, Pascalsches Dreieck
Auswahl und
Anwendung der
Formeln
Erstellung von
Baumdiagrammen
Lineare und quadratische Funktionen
Nutzen verschiedener
Darstellungsformen
(Tabelle, Graph,
Funktionsgleichung)
Wechselseitige
Beziehung zwischen
Realsituation und
Schaubild
Definieren, Ordnen und Beweisen
(z.B. an Vierecken, Satz des Thales)
Nutzen
mathematischen
Wissens für
Begründungen
Werkzeuge
Satz des Thales zur
Tangentenkonstruktion
Erkennen
entsprechender
Formeln in der
Umwelt und
Übertragung in
mathematische
Modelle zur
Berechnung
Formelsammlung/
Lexika
GTR /
Funktionenplotter
Dynamische
Geometrie Software
Curriculum Mathematik Jg. 9
Prozessbezogene Kompetenzen
Inhaltsbezogene Kompetenzen
Argumentieren/
Kommunizieren
Problemlösen
Modellieren
Quadratische Gleichungen
Quadratische Funktionen
Werkzeuge
GTR
Ähnlichkeitsbeziehungen (Vergrößern,
Verkleinern)
Argumentationsketten
Satz des Pythagoras, (Höhensatz,
Kathetensatz)
Stationenlernen
(optional)
Oberflächen und Volumen von Pyramiden,
Kegeln und Kugeln
Argumentationsketten; Überprüfung
und Bewertung von
von Problembearbeitungen
Potenzen, ganzzahlige Exponenten,
Logarithmus
Lesen und Schreiben
von Zehnerpotenzen
Zerlegen in
Teilprobleme
Mathematische
Modelle <-->
Realsituationen
Wählen geeigneter
Werkzeuge
(Geometriesoftware; GTR)
Umgang mit der
Formelsammlung
Exponentielle Funktionen im Kontext
(Wachstums- und Zerfallsprozesse,
Zinseszins)
Mathematische
Modelle <-->
Realsituationen
Sinus, Kosinus, Tangens im rechtwinkligen
Dreieck
Mathematische
Modelle <-->
Realsituationen
Sinusfunktion
Beschreibung
einfacher
periodischer
Vorgänge
Tabellenkalkulation;
GTR
Tabellenkalkulation