Zentrale Prüfung NRW 2015 Mathematik

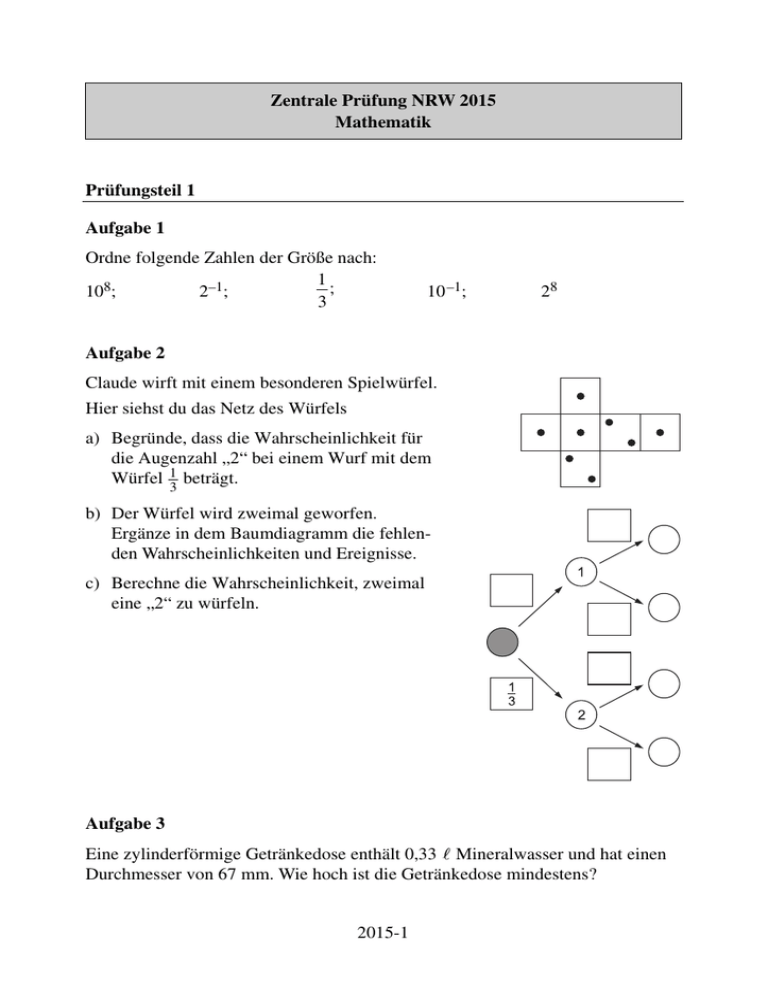
Zentrale Prüfung NRW 2015
Mathematik
Prüfungsteil 1
Aufgabe 1
Ordne folgende Zahlen der Größe nach:
1
;
108;
2–1;
3
10 –1;
28
Aufgabe 2
Claude wirft mit einem besonderen Spielwürfel.
Hier siehst du das Netz des Würfels
a) Begründe, dass die Wahrscheinlichkeit für
die Augenzahl „2“ bei einem Wurf mit dem
Würfel 13 beträgt.
b) Der Würfel wird zweimal geworfen.
Ergänze in dem Baumdiagramm die fehlenden Wahrscheinlichkeiten und Ereignisse.
c) Berechne die Wahrscheinlichkeit, zweimal
eine „2“ zu würfeln.
Aufgabe 3
Eine zylinderförmige Getränkedose enthält 0,33 ; Mineralwasser und hat einen
Durchmesser von 67 mm. Wie hoch ist die Getränkedose mindestens?
2015-1
Aufgabe 4
Löse folgendes Gleichungssystem mit einem geeigneten Verfahren:
(I)
2x + y = 2
(II) x − 0,5y = 2
Aufgabe 5
Bei einem Dreieck ABC ist die Seite AB
4 cm lang (vgl. Abbildung rechts). Der
Winkel α bei dem Punkt A ist 40° groß.
a) Bestimme rechnerisch die Länge der
Seite AC.
b) Bestimme rechnerisch die Länge der
Seite BC.
Skizze eines Dreiecks, nicht maßstabsgetreu
Aufgabe 6
Mit einer dynamischen Geometriesoftware werden zwei Geraden durch die
Punkte A und B bzw. C und D erzeugt. Die beiden Geraden haben den gemeinsamen Schnittpunkt S (vgl. Abbildung unten).
Was verändert sich, wenn du den Punkt A auf die Koordinaten (2 | 8) verschiebst? Begründe.
Bildschirmfoto aus einer dynamischen Geometriesoftware
2015-2
Lösung
Prüfungsteil 1
Aufgabe 1
r Hinweis: Bei negativen Exponenten gilt:
r −n 1
a =
r
an
Nebenrechnungen:
108 = 100 000 000
2 −1 =
1 1
= = 0,5
21 2
1
= 0,333…
3
1
1
10 −1 =
=
= 0,1
1
10
10
28 = 256
1
Lösung: 10 −1 < < 2 −1 < 28 < 108
3
Aufgabe 2
a) r Hinweis: Entnimm dem Netzbild des Spielwürfels die relevanten Daten
r zur Angabe der Wahrscheinlichkeit. Laut Formelsammlung gilt:
r
Anzahl der für E günstigen Ergebnisse
p(E) =
r
Anzahl aller möglichen Ergebnisse
Das Netz des Würfels besteht aus 6 gleich großen Flächen. Damit ist der
Wurf für jede Seite gleich wahrscheinlich. Da auf zwei Seiten die Augenzahl
„2“ und auf vier Seiten die Augenzahl „1“ steht, beträgt die Wahrscheinlichkeit, eine „2“ zu würfeln:
2 1
p(2) = =
6 3
2015-9