1. Hauptsatz der Thermodynamik W + Q = ΔU (1.Hauptsatz) IHV

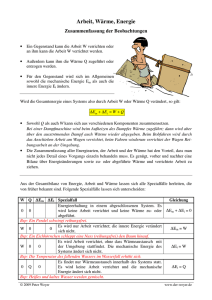
In der Physik und Technik wird häufiger mit der Masse m als mit der Stoffmenge n gerechnet.
Deshalb wird meist nicht mit der allgemeinen Gaskonstante R, sondern mit der spezifischen Gaskonstante R S
gearbeitet. Die spezifische Gaskonstante ist für jedes Gas, das näherungsweise als ideales Gas betrachtet wird
kann, eine Stoffkonstante. Sie hängt nicht vom Druck und von der Temperatur ab.
m
Ersetzt man in der Gleichung pV = nRT n durch
(M: molare Molekülmasse in gmol -1), dann erhält man:
M
pV = mRST mit RS =
Tafelwerk S. 15
R
M
z.B. Helium RS = 2077 Jkg -1 K -1
Luft
RS = 287 Jkg -1 K -1
Stickstoff RS = 297 Jkg -1 K -1
Wasserstoff RS = 4124 Jkg -1 K -1
1. Hauptsatz der Thermodynamik W + Q = ΔU (1.Hauptsatz)
IHV
Warum erwärmt sich eine verschlossene Luftpumpe, wenn der Kolben schnell nach unten gedrückt wird?
Warum kühlt sich das Ventil einer Gasflasche stark ab, wenn das Gas aus der Flasche entweicht?
Wie funktioniert ein Verbrennungsmotor?
Diese Fragen lassen sich mit Hilfe des 1. Hauptsatzes der Thermodynamik beantworten!
Um den 1. Hauptsatz der Wärmelehre zu verstehen, müssen wir den Begriff "innere Energie U" definieren.
Die Moleküle eines Gases besitzen Energie. Legen wir ein ideales Gas zu Grunde, so besteht
die Energie der Gasteilchen aus Translationsenergie. Andere Energieformen (chemische
Bindungsenergie, Kernenergie) sollen unberücksichtigt bleiben, da sie bei den von uns betrachteten
thermischen Prozessen unverändert bleiben.
Der thermische Anteil der inneren Energie U eines idealen Gases besteht nur aus der
kinetischen Energie (Translationsenergie) der Moleküle. Diesen wollen wir auch nur
betrachten.
m 2
v erkennen wir, dass die inneren Energie U eines Gases durch die
2
Masse der Gasmoleküle und deren Geschwindigkeit bestimmt wird. Eine Änderung der Geschwindigkeit der Moleküle ist
mit einer Temperaturänderung ΔT des Gases direkt verbunden.
Aus der Gleichung Ekin =
Eine Änderung der inneren Energie ΔU eines Gases erkennt man an der Änderung der Temperatur ΔT des Gases!
Treffen die Moleküle auf die Unterseite des beweglichen Kolbens, so können sie diesen anheben.
Das Gas verrichtet mechanische Arbeit W. Ein Teil der kinetischen Energie der Gasmoleküle wird über den Kolben
in Form von mechanischer Arbeit abgegeben. Dadurch wird die innere Energie des Gases um den Betrag ΔU
verringert. Die Temperatur T des Gases nimmt ab!
11
Welche Möglichkeiten gibt es, um die innere Energie U eines Gases zu verändern?
1. Möglichkeit:
IHV
Der Kolben soll unbeweglich sein.
Von außen wird über die Gefäßwand die Wärmemenge Q zugeführt. Die Temperatur T
steigt. Die innere Energie U nimmt um den Betrag ΔU = Q zu! (Q>0)
Die Moleküle werden schneller.
Bei Kühlung von außen wird dem Gas die Wärmemenge Q entzogen. Die innere Energie
nimmt um den Betrag ΔU = Q ab. (Q<0) Die Temperatur T sinkt.
Die Moleküle werden langsamer.
2. Möglichkeit:
Über die Gefäßwände soll keine Wärme Q ausgetauscht werden.
Mit einer Kraft F wird der Kolben nach unten gedrückt. Durch die Bewegung gegen die
Gasmoleküle werden diese vom Kolben angestoßen. Sie werden schneller. Dazu muss
am Kolben die Arbeit W verrichtet werden.
Die innere Energie U nimmt um den Betrag ΔU = W zu (W>0). Die Temperatur steigt an.
Wird der Kolben durch die kinetische Energie der Gasmoleküle weggeschoben,
nimmt die innere Energie um den Betrag ΔU = W ab (W<0). Die Temperatur nimmt ab.
Es können auch beide Möglichkeiten gleichzeitig ablaufen. Diese werden im 1. Hauptsatz der Wärmelehre
zusammengefasst:
Tauscht ein System mit seiner Umgebung die Wärme Q aus, verrichtet es mechanische Arbeit W oder
wird an ihm mechanische Arbeit verrichtet, dann ändert sich seine innere Energie U.
Die Änderung der inneren Energie ΔU ist gleich der Summe aus mechanischer Arbeit W und ausgetauschter Wärme Q.
Es gilt:
ΔU = W + Q
Festlegung für die Vorzeichen:
Große Bedeutung hat der 1. Hauptsatz der Wärmelehre für die Berechnung von Abläufen in Wärmekraftmaschinen.
(Dampfmaschine, Dieselmotor, Ottomotor, Stirlingmotor)
In Wärmekraftmaschinen wird dem Arbeitsgas von außen Wärme zugeführt, die in Form von mechanischer Arbeit
wieder nach außen abgegeben wird.
Wir wollen diese Prozesse genauer untersuchen.
Berechnung der mechanischen Arbeit W:
1. Mechanische Arbeit bei konstantem Volumen (isochore Erwärmung oder Abkühlung)
Der einfachste Fall liegt vor, wenn das Volumen konstant bleibt. Der Kolben bewegt sich nicht.
Es wird also keine Arbeit verrichtet. Die zugeführte bzw. abgegebene Wärme führt ausschließlich
zu einer Veränderung der inneren Energie des Gases.
Aus ΔU = W + Q wird mit W = 0
Q = mcvΔT und somit auch
ΔU = Q
ΔU = mcvΔT (cv: spezifische Wärmekapazität des Gases
bei konstantem Volumen)
12
2. Mechanische Arbeit bei konstantem Druck p (isobare Expansion und Kompression) IHV
Dem Gas wird von außen die Wärme Q zugeführt. Die kinetische Energie
der Teilchen nimmt zu. Das Gas dehnt sich aus und schiebt den Kolben
mit konstanter Kraft F um die Wegstrecke Δs nach außen.
Der Druck p im Zylinder bleibt konstant, da sich das Gas ausdehnen kann.
Für die verrichtete Arbeit W gilt:
F
folgt F = p·A
A
( A ist die Kreisfläche des Kolbens)
W = p·A· Δs ,wobei ΔV = A· Δs (Volumenformel Kreiszylinder)
W = F·Δs
Aus der Druckgleichung p =
W = p· ΔV
mit
ΔV = VEnde - VAnfang > 0 (Expansion)
ΔV = VEnde - VAnfang < 0 (Kompression)
Da das Gas Energie in Form von Arbeit nach außen abgibt, erhält die Gleichung ein negatives Vorzeichen.
W = - p· ΔV
Da sich durch die Arbeit W das Volumen des Gases verändert, wird sie auch als Volumenarbeit bezeichnet.
Darstellung im V-p-Diagramm:
Im Diagramm ist die isobare Kompression
dargestellt. (V1 > V2)
Die Arbeit W entspricht der Maßzahl der Fläche,
die die waagerechte Gerade durch p im Intervall
von V1 bis V2 mit der V-Achse einschließt.
Die vom Gas aufgenommene oder an die Umgebung abgegebene Wärme Q kann mit der Gleichung
Q = m·cp· ΔT
berechnet werden. (cp: spezifische Wärmekapazität des Gases bei konstantem
Volumen)
Es ergibt sich: ΔU = Q + W = mcpΔT + (- pΔV)
(selbständige Erarbeitung mit AB)
Man kann eine isobare Zustandsänderung modellhaft in drei Teilschritte zerlegen:
a) Dem Gas wird bei konstantem Druck Wärme zugeführt: Q = mcpΔT
b) Durch die Wärmezufuhr erhöht sich zunächst die
innere Energie des Gases bei konstantem Volumen:
ΔU = mcvΔT
c) Anschließend führt die Temperaturerhöhung im Gas
zu einer Expansion, bei der von Gas mechanische
Arbeit verrichtet wird:
W = - pΔV
In der Realität laufen alle 3 Prozesse gleichzeitig ab. Damit ergibt sich aus dem 1. Hauptsatz:
ΔU = Q
+
W
mcvΔT = mcpΔT + (- pΔV)
Bei der isobaren Zustandsänderung wird ein Teil der zugeführten Wärme Q durch die Ausdehnung
in Form von mechanischer Arbeit wieder abgegeben, bei der isochoren Zustandsänderung aber nicht.
Deshalb ist cp > cv!
13
Universelle Gasgleichung und 1. Hauptsatz:
ΔU = Q
ΔU = Q
Es ergibt sich:
+
W
+ (- pΔV)
ΔU = Q
-
pΔV
ΔU = Q
-
nRΔT
Bei der isobaren Zustandsänderung ist W = - pΔV.
universelle Gasgleichnung: pV = nRT
bzw:
pΔV = nRΔT
Aufgabe: In einem Zylinder mit beweglichem Kolben sind 5 kg trockene Luft eingeschlossen.
Welche Arbeit wird verrichtet, wenn diese Luft im Zylinder von 15° C auf 60° C erwärmt wird?
geg: m = 5 kg
1 = 15° C
2= 60° C  ΔT = 45 K
cp = 1,01 kJkg -1K -1
cV = 0,72 kJkg -1K -1
ges: W
Lösung: ΔU = Q +
W
mcvΔT = mcpΔT +
W
W = mcvΔT - mcpΔT
W = m ΔT(cv - cp) = 5 kg*45 K*(0,72 - 1,01) kJkg -1K -1 = - 65,3 kJ
Das negative Vorzeichen bedeutet: Es wird Arbeit vom Gas verrichtet.
3. Mechanische Arbeit bei konstanter Temperatur (isotherme Expansion und Kompression) IHV
Eine in einer Luftpumpe eingeschlossene Luftmenge wird durch langsames Hineindrücken des Kolbens
von 80 cm 3 auf 20 cm 3 komprimiert. Der anfängliche Druck beträgt 1000 hPa.
Die Temperatur gleicht sich durch die Langsamkeit an die Umgebungstemperatur an. (T = konstant)
Es gilt: pV = konstant = p1V1 = 100*10 3 Nm -2*8*10 -5 m 3 = 8 Nm (oder 80000 hPa cm 3)
p(V) = 8 Nm*
1
V
Durch Rechnung ergibt sich:
V in cm 3
p in hPa
80
1000
60
1333
40
2000
20
4000
Damit erhält man folgendes Diagramm:
Wie bei der isobaren Zustandsänderung gilt auch hier: Die Fläche entspricht der Arbeit W!
Da die Fläche jetzt aber krummlinig begrenzt wird, kann sie entweder nur durch Auszählung bestimmt oder
mit Hilfe der Integralrechnung berechnet werden.
Die Auszählung ergibt:
W ≈ 11 Nm
V2
Aus der Integralrechnung folgt: W = - 
p(V) dV mit p(V) =
V1
14
p1V1
V
V2
p1V1
W=-
 V dV
V2
1
= - p1V1  dV
V
V1
V1
W = - p1V1 [ ln V ]
V2
V1
W = - p1V1 ( ln V2 - ln V1)
W = - p1V1 ln
V2
= - 8 Nm*(- 1,39) = 11,1 Nm
V1
Die mechanische Arbeit W bei der isothermen Zustandsänderung lässt sich mit der Gleichung
W = - pV ln
V2
V1
berechnen.
Da die Temperatur konstant bleibt, ändert sich die innere Energie des Gases nicht!
ΔU = 0
 0 = Q + W oder W = - Q
Die adiabatische Zustandsänderung
Bei der adiabatischen Zustandsänderung erfolgt kein Wärmeaustausch mit der Umgebung.
(totale Wärmeisolation der Wände oder der Prozess läuft sehr schnell ab)
Schnell ablaufende Prozesse finden in Verbrennungsmotoren (z.B. Dieselmotor) oder Kompressoren statt.
Es gilt also: Q = 0 und somit ΔU = W
Die Temperatur verändert sich erheblich.
Es gelten folgende Gesetzmäßigkeiten:
pV κ = konstant bzw. p1V1 κ = p2V2 κ
(κ: kappa ist der Adiabatenexponent und
5
beträgt für einatomige Gase κ =
3
7
bzw.
für zweiatomige Gase κ = )
5
T1
V2
= ( ) κ-1
T2
V1
und
T1
p1 κ - 1
=( ) κ
T2
p2
Die molaren Wärmekapazitäten Cm,v und Cm,p
Um die Gleichungen Q = mcvΔT und Q = mcpΔT nutzen zu können, muss die Masse des eingeschlossenen
Gases bekannt sein. Oft ist aber nur die Stoffmenge des Gases gegeben oder über die Formel pV = nRT
bestimmbar. Ist bekannt, ob es sich um ein - oder zweiatomiges ideales Gas handelt, dann kann Q auch über
die molaren Wärmekapazitäten Cm,v und Cm,p bestimmt werden. (siehe Gedankenexperiment von Mayer)
Es gilt dann:
isochore Zustandsänderung
3
R (einatomige Gase)
2
5
Cm,v = R (zweiatomige Gase)
2
7
Cm,v = R (mehratomige Gase)
2
isobare Zustandsänderung
5
Qp = n Cm,pΔT
mit Cm,p = R (einatomige Gase)
2
7
Cm,p = R (zweiatomige Gase)
2
QV = n Cm,v ΔT
mit Cm,v =
Cm,p =
9
R (mehratomige Gase)
2
15
Gedankenexperiment von J. R. Mayer IHV
In der nachfolgenden Skizze sind zwei gleichgroße zylinderförmige Behälter B1 und B2 abgebildet,
die beide durch gleichschwere Kolben K abgeschlossen sind. Jeder Behälter ist mit der gleichen Menge
eines bestimmten Gases gefüllt, das als ideales Gas betrachtet werden soll.
Mit dieser Anordnung kann nach einer Idee von J. R. Mayer aus dem Jahre 1842 ein Gedankenexperiment
durchgeführt werden.


Durch Zuführung von Wärme wird die Temperatur der Gase in den beiden Behältern jeweils um
den gleichen Betrag ΔT erhöht.
Die Kolbenbewegung wird in B1 verhindert, während der Kolben in B2 reibungsfrei gleiten kann.
Den Gassystemen in den Behältern B1 (konstantes Volumen) und B2 (konstanter Druck) werden die
Wärmemengen QV und Qp zugeführt, so dass ihre Temperatur um den gleichen Betrag ΔT steigt.
Damit nimmt die innere Energie beider Systeme um den gleichen Betrag ΔU zu.
Trotzdem zeigt sich, dass dem Behälter B2 eine größere Wärmemenge zugeführt werden muss, da vom System
zusätzlich mechanische Arbeit W verrichtet wird.
Der Wert dieser Arbeit W entspricht der Differenz Q p - QV.
Dies entspricht der Aussage von J. R. Mauer, dass Wärme und Arbeit zwei äquivalente Prozessgrößen sind,
die die Energieübertragung zwischen Systemen realisieren können.
Mit dem 1. Hauptsatz folgt:
B1:
B2 :
ΔU = QV
ΔU = Qp + W, W < 0
QV = Qp + W
bzw. W = Qp - QV.
Qp - QV
= p·ΔV
(Cm,p - Cm,V )·n·ΔT = p·ΔV
(Cm,p - Cm,V )·n·ΔT = n·R·ΔT
mit Qp = n·Cm,p·ΔT und QV = n·Cm,V·ΔT
→ R = Cm,p - Cm,V
(universelle Gaskonstante)
Aufgabe: In jedem Behälter befinden sich 0,5 mol Luft (Cm,p = 29,10 Jmol -1K -1, Cm,V = 20,77 Jmol -1K -1),
deren Temperatur jeweils um ΔT = 10 K erhöht werden soll.
Berechnen Sie in beiden Fällen die erforderliche Wärme und begründen Sie den Unterschied zwischen
dem Tabellenwert von R und dem aus den Wärmekapazitäten der Luft resultierenden Werte.
Lösung:
Qp = n·Cm,p·ΔT = 0,5 mol·29,10 Jmol -1K -1·10 K = 145,5 J
QV = n·Cm,V·ΔT = 0,5 mol·20,77 Jmol -1K -1·10 K = 103,85 J
R = Cm,p - Cm,V = 8,33 Jmol -1K -1
Luft als Gemisch verschiedener Gase entspricht nur näherungsweise einem idealen Gas,
während sich der Tabellenwert auf das ideale Gas bezieht.
16
Zusammenfassung:
4-Takt-Ottomotor oder anschauliche Animation
Dampfmaschine
Beim Ottomotor wird im Vergaser ein BenzinLuftgemisch erzeugt oder das Benzin direkt
eingespritzt.
Das Benzin-Luftgemisch wird über den Zündfunken einer Zündkerze gezündet.
17
4-Takt-Dieselmotor
Die im Zylinder angesaugte Luft wird so stark verdichtet,
dass ihre Temperatur auf 500° C bis 700° C steigt.
Bei dieser Temperatur wird der Diesel mithilfe einer
Einspritzpumpe in den Zylinder eingespritzt.
Der Treibstoff entzündet sich selbst bei dieser Temperatur.
(Zweitaktmotor, Wankelmotor)
Bestimmung des mechanischen Wärmeäquivalents
IHV
Aus dem 1. Hauptsatz der Wärmelehre ergibt sich, dass mechanische Arbeit in Wärme und Wärme
in mechanische Arbeit umgewandelt werden kann.
Wärme und mechanische Arbeit sind also energetisch betrachtet zueinander äquivalente Größen.
J.P. Joule ermittelte experimentell das mechanische Wärmeäquivalent mit erstaunlicher Genauigkeit.
Infolge der Gewichtskraft sinkt das Massestück nach unten und
verrichtet Arbeit am Rührwerk.
Zugleich verringert sich dabei seine potenzielle Energie entsprechend.
Durch das Umrühren der Flüssigkeit vergrößert sich deren Temperatur.
Es wird also durch die mechanische Arbeit der gleiche Effekt erzielt
wie durch direkte Zufuhr von Wärme.
Aufgabe: Wie groß ist die Temperaturerhöhung, wenn sich im Gefäß 100 ml Wasser befinden, das
Massestück 5 kg schwer ist und 2 m herabsinkt?
(Reibungseffekte an der mechanischen Aufhängung werden vernachlässigt.)
geg: mW = 0,1 kg (V = 100 ml)
mG = 5 kg
h = 2,0 m
g = 9,81 ms -2 cW = 4,19 kJkg -1K -1
Lösung:
ges: ΔT
W
= Q
mG gh = mW cW ΔT
ΔT =
mG gh
5 kg*9,81 ms -2*2,0 m
=
= 0,23 K
mW cW 0,1 kg*4,19*10 3 Nmkg -1 K -1
Unter den gegebenen Bedingungen würde sich das Wasser um 0,23 K erwärmen.
18
Zustandsgröße Entropie S; Q = T·ΔS
IHV
Reversible und irreversible Vorgänge
Während die eine Kugel annähernd wieder ihren Ausgangszustand erreicht,
bleibt die andere Kugel am Boden liegen.
Vorgänge in Natur und Technik, die von einem Ausgangszustand aus
von allein wieder zu diesem Ausgangszustand führen, bezeichnet man
als reversible Vorgänge.
Beispiele für näherungsweise reversible Vorgänge:
- Sprünge einer elastischen Kugel,
- Bewegung eines Federschwingers,
- Bewegung der Erde um die Sonne,
Vorgänge in Natur und Technik, die von einem Ausgangszustand aus unbeeinflusst in einer bestimmten
Richtung ablaufen und bei denen von allein der Ausgangszustand nicht wieder erreicht wird, nennt
man irreversible Vorgänge.
Beispiele für irreversible Vorgänge:
- Abbremsen eines Autos,
- Abkühlung von Körpern auf Umgebungstemperatur,
- Durchmischung von Gasen,
Auch bei irreversiblen Vorgängen lässt sich der Ausgangszustand wieder herstellen. Das sind aber Vorgänge,
die nicht von allein erfolgen.
Betrachtet man reversible und irreversible Vorgänge aus energetischer Sicht, dann genügen sie alle dem
Energieerhaltungssatz und dem 1. Hauptsatz der Thermodynamik.
Der Energieerhaltungssatz erlaubt keine Entscheidung darüber, ob ein Vorgang reversibel oder
irreversibel ist!
Um die Irreversibilität eines konkreten Prozesses genauer beschreiben zu können, ist die Einführung
einer neuen Größe erforderlich. Diese Größe ist die Entropie.
Entropie
Formelzeichen: S
Einheit: 1
J
K
Entropie bei Durchmischung: Beispiel Verteilung von Gasteilchen
Nach Entfernen der Trennwand werden
sich die Gasteilchen im gesamten Volumen
V2 ausbreiten, wobei eine Gleichverteilung
die wahrscheinlichste Verteilung ist.
Die Wahrscheinlichkeit, dass sich alle
Teilchen wieder gleichzeitig im Volumen V1
befinden, ist äußerst gering. Diese
Wahrscheinlichkeit lässt sich berechnen.
Ein zufällig herausgegriffenes Teilchen befindet sich mit einer Wahrscheinlichkeit von w2 = 1 im Gesamtvolumen
V2. Die Wahrscheinlichkeit, es im halb so großen Volumen V1 anzutreffen, ist nur w1 = 1/2.
1 1
1
· = ( )2
2 2
2
Für zwei Teilchen gilt:
w1 =
Für N Teichen gilt:
w1 = (
1 N
)
2
Allgemein gilt: Ist w1 die Wahrscheinlichkeit für einen Ausgangszustand und w 2 die Wahrscheinlichkeit für einen
w2
Endzustand, dann gibt das Verhältnis W =
an, wie viel mal wahrscheinlicher der Endzustand
w1
als der Ausgangszustand eintreten wird.
Für die Änderung der Entropie ΔS gilt dann: ΔS ~ ln W
Merkmale für irreversible Vorgänge:
1. Wärme wird an die Umgebung abgegeben.
2. Das System gelangt in einen Zustand größerer Unordnung.
3. Die Energie und die Teilchen des Systems streben der wahrscheinlichsten
Verteilung, der Gleichverteilung, zu.
19
Entropie bei isothermen Vorgängen:
IHV
Den Zusammenhang ΔS ~ ln W kann man zwar für quantitative Betrachtungen, nicht aber für praktikable Messungen
der Entropieänderung verwenden.
Bei der isothermen Zustandsänderung ergibt sich eine Messvorschrift aus folgender Überlegung:
Ein heißer Körper der Temperatur T gibt Wärme an ein Gas in einem
Zylinder ab. Der frei bewegliche Kolben verschiebt sich. Die Gasteilchen
verteilen sich auf einen größeren Raumbereich, die Entropie nimmt zu.
Je mehr Wärme vom Gas aufgenommen wird, desto weiter dehnt sich das
Gas aus und desto stärker nimmt seine Entropie zu.
Es gilt:
ΔS ~Q, wobei Q die Wärme ist, die das System bei einer bestimmten Temperatur T aufnimmt
oder abgibt.
Für isotherme Zustandsänderungen (auch Aggregatzustandsänderungen) gilt die Gleichung:
ΔS =
Q
T
Aufgabe: Wie groß ist die Entropieänderung beim Schmelzen von 1 kg Eisen?
(Ergebnis: ΔS = 0,15 kJK -1)
2. Hauptsatz der Thermodynamik (Entropiesatz)
Während der 1. Hauptsatz der Thermodynamik eine Aussage über energetisch mögliche Prozesse macht,
gibt der 2. Hauptsatz der Thermodynamik Auskunft über die Richtung von Prozessen in abgeschlossenen
Systemen, die sich selbst überlassen sind.
2. Hauptsatz der Wärmelehre: In einem abgeschlossenen System verlaufen die natürlichen
Vorgänge immer so, dass die Entropie zunimmt.
andere Formulierungen: Ein Perpetuum mobile 2. Art ist unmöglich. (Perpetuum mobile 1.Art)
oder: Die Natur strebt aus einem unwahrscheinlicheren dem
wahrscheinlicheren Zustand zu.
Setzt man das Universum als ein abgeschlossenes System voraus, so nimmt bei allen Naturvorgängen die
Entropie des Weltalls ständig zu. Die Welt strebt damit einem Zustand der völligen Gleichverteilung aller
Energie zu. Bei dem schließlich zu erwartenden vollständigen Temperaturausgleich ist keine Energieumwandlung
und damit keine Veränderung mehr möglich. Man spricht vom Wärmetod des Weltalls.
Es lässt sich aber mit Sicherheit nicht sagen, ob das Universum ein abgeschlossenes System darstellt.
Auf offene Systeme lässt sich der 2. Hauptsatz nicht übertragen.
Wärmepumpen:
Wärmepumpen und Kühlschränke besitzen den gleichen
prinzipiellen Aufbau. Beim Kühlschrank wird aber die
Wärme von innen nach außen, bei der Wärmepumpe von
außen nach innen transportiert.
Ausgenutzt wird die bei unterschiedlichem Druck
unterschiedliche Siede- beziehungsweise Kondensationstemperatur einer Flüssigkeit.
Im Verdampfer wird Unterdruck erzeugt. Die Flüssigkeit
verdampft bei schon geringer Temperatur und entzieht dabei
der Umgebung Wärme. Im Verflüssiger kondensiert die
Flüssigkeit bei Überdruck und kann deshalb die Wärme bei
höherer Temperatur abgeben.
Das Temperaturgefälle zwischen dem Innen- und Außenraum nimmt zu (unwahrscheinlicherer Zustand).
Die Entropie nimmt ab. Um diesen Zustand zu erreichen, muss der Kompressor aber Arbeit verrichten
(führt zu einer Entropiezunahme). Betrachtet man beide Prozesse, so kommt es insgesamt zu einer
Entropiezunahme. Der 2. Hauptsatz bestätigt sich.
20