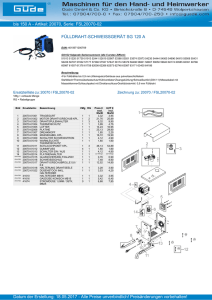
KAPITEL E - bei DuEPublico

Grundlagen der Physik I
Mechanik
Vorlesungsskript
A. Stampa
Universität GH Essen
(Version 1999)
1
INHALT
KAPITEL A: Einleitung
Seite
1. Was ist Physik?
6
2. Messen, Einheiten
8
a) Größen und Zahlenwerte
8
b) Zugeschnittene Größengleichung
9
c) Grundeinheiten im SI - System
9
3. Bemerkungen zu Fehlern
10
KAPITEL B: Kinematik
12
1. Die geradlinige Bewegung
12
a) Geschwindigkeit als Ableitung
12
b) Differenziationsregeln
14
c) Beispiel: die harmonische Schwingung
15
d) Ermittlung des Weg - Zeit - Gesetzes durch Integration
17
e) Geradlinige Bewegung mit konstanter Beschleunigung
19
2. Die krummlinige Bewegung von Teilchen
21
a) Vektoren
21
b) Einige Operationen mit Vektoren
22
c) Realisierung von Vektoraddition: Überlagerung von Bewegungen 22
d) Die Geschwindigkeit bei krummliniger Bewegung
24
e) Produkte von Vektoren
26
f) Beispiele für krummlinige Bewegung
30
α) Der waagerechte Wurf
30
β) Die gleichförmige Kreisbewegung
31
γ) Die Winkelgeschwindigkeit als Vektor
34
δ) Der schiefe Wurf
35
g) Approximation von Kurven
38
KAPITEL C: Dynamik von Massenpunkten
42
1. Die Newtonschen Axiome
42
a) Newtons Formulierung der Axiome
42
b) Das Trägheitsprinzip
42
c) Das Aktionsprinzip
43
α) Definition einer Kraftskala
43
β) Zerlegung von Kräften
44
d) Das Reaktionsprinzip
46
e) Historische Randbemerkungen
47
2. Kräfte
48
a) Die Grundkräfte
48
b) Die Gravitation
49
c) Kraft zwischen ausgedehnten Körpern
52
α) Integration über Massenelemente
52
β) Feldstärke
53
γ) Der Fluß
53
δ) Das Gesetz von Gauß
55
2
d) andere Grundkräfte
57
e) Kräfte zwischen makroskopischen Körpern
59
α) Kraft durch elastische Verformung
59
β) Reibungskraft
60
3. Beispiele für einfache Bewegungen
62
a) In zäher Flüssigkeit fallende Kugel
62
b) Reibungsfreie Bewegung auf einer schiefen Ebene
64
c) Die Atwoodsche Fallmaschine
65
d) Die Rakete
66
e) Dynamik der Kreisbewegung
67
f) Geladenes Teilchen im Magnetfeld
68
g) Kurvenneigung
69
h) Das Geoid
69
4. Drehimpuls und Drehmoment
70
a) Der Drehimpuls
70
b) Das Drehmoment
71
c) Der Flächensatz
72
5. Arbeit, Leistung, Energie
74
a) Grundbegriffe
74
b) Berechnung des Integrals ∫ F • ds
75
c) Die potentielle Energie
77
α) Was ist potentielle Energie?
77
β) Äquipotentialflächen
79
γ) Das Vorzeichen
80
δ) Arbeit im Potentialfeld
80
ε) Das Potential
81
η) Potentialkurven
82
d) Die Kinetische Energie
84
e) Der Energiesatz der Mechanik
86
f) Verschiedene Energieformen
86
g) Anwendung des Energiesatzes
87
α) Der Looping
87
β) Der harmonische Oszillator
88
γ) Das Fadenpendel
90
δ) Anwendung des Energiesatzes bei Anwesenheit von Reibung 91
ε) Leistung in einer Strömung
92
ζ) Ausströmgeschwindigkeit
92
h) Kraft bei mehrdimensionalen Potentialen
93
6. Das Keplerproblem
94
a) Historisches
94
b) Einige Eigenschaften von Kegelschnitten
97
c) Herleitung der Bahngleichung
100
7. Scheinkräfte
104
a) Was sind Scheinkräfte
104
b) Scheinkräfte im rotierenden System
106
α) Formale Herleitung
106
β) Die Zentrifugalkraft
109
3
γ) Die Corioliskraft
KAPITEL D: Dynamik von Massenpunktsystemen
1. Der Massenmittelpunkt
a) Das Hebelgesetz
b) Der Schwerpunkt beliebiger Massenpunktsysteme
c) Schwerpunkt als Mittelwert
d) Schwerpunkt kontinuierlicher Massenverteilungen
α) Übergang von diskreten zu kontinuierlichen Massen
β) Das Massenelement
γ) Wie berechnet man Volumenintegrale?
2. Bewegung des Schwerpunktes
a) Das Aktionsgesetz
b) Das Zweikörperproblem, reduzierte Masse
3. Dynamische Hilfsbegriffe
a) Der Impuls
b) Der Drehimpuls
c) Energie
4. Stoßgesetze
a) Was ist ein Stoß?
b) Grundbegriffe
c) Elastischer zentraler Stoß
d) Stoß mit seitlicher Impulsänderung
e) Der inelastische Stoß
KAPITEL E: Mechanik von Flüssigkeiten und Gasen
1.Vorbemerkungen über Gase, Flüssigkeiten und feste Körper
2. Druck in Gasen
3. Hydrostatik
a) Das Eigengewicht ist vernachlässigbar
b) Druck aufgrund des Eigengewichtes
c) Auftrieb
d) Die Barometrische Höhenformel
e) Die Oberflächenspannung
4. Hydrodynamik
a) Das Geschwindigkeitsfeld
α) Grundbegriffe
β) Der Fluß
γ) Die Kontinuitätsgleichung
δ) Anzahl der Stromlinien
b) Die Bewegungsgleichung
c) Der Satz von Bernoulli
d) Innere Reibung von Flüssigkeiten
α) Was ist Viskosität?
β) Die Grenzschicht
γ) Die stationäre Rohrströmung
δ) Das Stokesche Gesetz
ε) Die Reynoldszahl
KAPITEL F: Mechanik starrer Körper
110
113
113
113
114
115
116
116
117
118
121
121
122
124
124
124
128
129
129
130
130
134
135
137
137
137
140
140
141
142
144
146
150
150
150
150
151
151
152
153
157
157
158
159
161
162
164
4
1. Das Modell des starren Körpers
164
2. Statik
164
3. Grundbegriffe zur Beschreibung einer Rotation
167
a) Das Trägheitsmoment
167
b) Der Drehimpulsvektor
168
c) Berechnung des Trägheitsmomentes
170
4. Beispiele zur Bewegung starrer Körper
176
a) Achse raum- und körperfest, äußeres Drehmoment konstant
176
b) Achse körperfest, wird bei der Bewegung parallel verschoben 177
c) Achse körperfest, kein äußeres Drehmoment
178
d) Achse körperfest, Drehmoment senkrecht zu L
179
e) Anwendungen der Kreiselgesetze
181
α) Wendeanzeiger
181
β) Der Kreiselkompaß
181
γ) Der Spielkreisel
181
δ) Dynamische Stabilisierung des Fahrrads
182
KAPITEL G: Schwingungen
183
1. Allgemeines
183
2. Die harmonische Schwingung
183
a) Darstellung
183
b) Die Kinematik der harmonischen Schwingung
184
c) Schwingung eines Massenpunktes
185
d) Die Schwingung eines ausgedehnten Körpers
188
3. Überlagerung von Schwingungen gleicher Frequenz
191
a) Anwendung der Additionstheoreme
191
b) Zeigerdiagramm
192
c) Beispiele
193
4. Schwingung als komplexe Zahl
194
a) Komplexe Zahl
194
b) Algebraische Operationen mit komplexen Zahlen
195
c) Satz von Moivre
196
d) Anwendung der komplexen Zahlen auf Schwingungsprobleme 197
5. Die gedämpfte Schwingung
199
a) Die freie gedämpfte Schwingung
199
b) Die erzwungene Schwingung
201
6. Überlagerung bei ungleicher Frequenz oder Richtung
205
a) Schwebungen
205
b) Überlagerung von Schwingungen und ihren Oberschwingungen207
c) Überlagerung bei verschiedenen Schwingungsrichtungen
209
KAPITEL H: Spezielle Relativitätstheorie
211
1. Einleitung
211
a) Womit befaßt sich die Relativitätstheorie?
211
b) Der Äther
212
c) Versuche zur Bewegung der Erde durch den Äther
212
2. Aufbau der Relativitätstheorie
215
a) Die Grundpostulate
215
b) Direkte Folgerungen der Grundpostulate
215
α) Die Gleichzeitigkeit ist relativ
215
5
β) Gleich gebaute Uhren gehen nicht gleich schnell
γ) Längen werden unterschiedlich gemessen
c) Lorentztransformation
α) Herleitung der Transformationsformeln
β) Diskussion
d) Minkowski Diagramme
α) Was sind Minkowski Diagramme?
β) Zeitdilatation und Längenkontraktion im Minkowski Diagr.
γ) Gegenwart, Vergangenheit, Zukunft
δ) Der relativistische Dopplereffekt
ε) Ein Zwillingsparadoxon
e) Experimente mit Uhren
f) Experimente mit Elementarteilchen
g) Andere Evidenzen
216
217
218
218
220
227
228
229
229
231
231
233
234
235
6
KAPITEL A
Einleitung
1. Was Ist Physik?
Die Physik beschäftigt sich mit der unbelebten Natur, wobei im Gegensatz zur Chemie Änderungen der Stoffzusammensetzung weniger interessieren. Man erwartet von der Physik,
daß sie erklärt, wobei eine "Erklärung" sehr subjektiv ist. Z.B. finden manche Menschen, einen Sachverhalt als gut erklärt, wenn er auf das typische Verhalten von Menschen zurückgeführt wird: Die rollende Kugel kommt zum Stillstand, weil sie erschöpft ist. Andere verlangen eine mechanische Erklärung, etwa die Gravitationskraft als hervorgerufen durch den
Stoß vieler kleiner Teilchen. In der Physik soll eine Erklärung ein konsistentes Bild liefern
und Ereignisse vorhersagen. Die Anzahl der nicht beweisbaren Annahmen soll möglichst
klein sein, und das Gedankengebäude soll schön sein.
Aristoteles erklärte den Fall eines Steines, indem er sagte, jeder Körper ist bestrebt, den ihm
in der Welt zustehenden Platz einzunehmen. Damit wird der Fall erklärt und das Aufsteigen
leichter Gase. Das Verhalten von Mondmaterie auf der Erde wäre wahrscheinlich falsch vorhergesagt worden. Ebenso wurde die Geschwindigkeit beim freien Fall und der waagerechte
Wurf falsch vorhergesagt. Der Mangel an Erfolg in der der antiken griechischen Physik liegt
wahrscheinlich daran, daß die Kraft des Denkens überschätzt wurde.
Die Methode der Erkenntnisfindung in der Physik seit Galilei besteht aus zwei Elementen:
Dem Aufbau eines gedanklichen Modells, und der Überprüfung an der Wirklichkeit. Dieses
Wechselspiel von Hypothese und Experiment ist ein sehr universelles Verfahren, das alle Lebewesen zum Sammeln von Information über die Welt anwenden: In der Evolution geht man
davon aus, daß die Information in der Erbsubstanz codiert ist. Durch Mutation der Erbsubstanz wird als "Hypothese" eine neue Variante der Art vorgeschlagen. Wenn sie sich nicht
bewährt, stirbt sie aus. Das Experiment ist negativ ausgefallen. Wenn sie sich bewährt, wird
sie sich durchsetzen. Sie enthält im allgemeinen eine bessere Information über die Umwelt.
In diesem Fall entscheidet das Experiment über Leben und Tod. Beim Menschen gibt es im
täglichen Leben diese "harte" Überprüfung einer Hypothese etwa beim Überholmanöver. In
der Mehrheit der Fälle entscheidet die Überprüfung nicht unmittelbar über Leben und Tod,
sondern nur über die Richtigkeit der zugrunde gelegten Gesetze und Annahmen. Ein negativer Ausgang eines wichtigen Experimentes läßt erwarten, daß das Weltbild geändert wird.
7
Häufig bleibt die ursprüngliche Version des Weltbildes als Näherung des neuen gültig. Ein
Experiment, das anders als vorhergesagt verläuft, ist also keine Schande, sondern im allgemeinen ein Erfolg.
Man erkennt in der Geschichte der Physik Phasen, in denen die Entwicklung der Physik stark
behindert wurde, weil entweder das Experiment (die induktive Methode) oder die Theorie
(die deduktive Methode) überbewertet wurde. Ende des 19. Jahrhunderts haben sich die Positivisten mit Ernst Mach als prominenten Vertreter aus der Physik dafür eingesetzt, sich nur
mit Dingen zu beschäftigen, die beobachtbar sind. Dadurch ist die Entwicklung der
Atomtheorie und Kernphysik in Deutschland behindert worden. Heute scheut man sich nicht,
von Quarks als kleinsten Bausteinen der Materie zu sprechen und gleichzeitig zu fordern, daß
sie niemals einzeln in Erscheinung treten.
Oft wird von der Physik erwartet, daß sie eine Formel bereit hat, mit der es möglich ist, den
Lauf der Welt genau zu beschreiben. Dies kann die Physik nicht, denn
Man kennt diese Weltformel nicht. Man kennt nur eine näherungsweise Beschreibung der
Welt. Nur die Grenze der Ignoranz verschiebt sich.
Man kennt den augenblicklichen Zustand der Welt nicht. Im mechanischen Weltbild müßte man Ort und Geschwindigkeit aller Teilchen zu einem bestimmten Zeitpunkt kennen,
um ihr Verhalten für alle Zeiten vorhersagen zu können.
Weniger bekannt ist vielleicht, daß die qualitative Argumentation in der Physik eine wichtige
Rolle spielt.
Beispiel:
Warum sind bei großen Vögeln die Flügel lang und schmal, bei kleinen kurz und breit?
Argumentation: Die Auftriebskraft wird proportional der Fläche der Flügel sein, d.h (s.
Abb.1)
F A ∼ A ∼ LB
8
Abb. 1: Große Vögel haben im allgemeinen im Verhältnis
zur Körperlänge lange Flügel
Die Gewichtskraft wird proportional zum Volumen des Körpers sein und diese ist bei gleicher Gestalt proportional zu l3, wenn l die Länge des Körpers ist, also zu B3.
FG ∼ V ∼ B3
Da der Auftrieb die Gewichtskraft kompensieren muß, gilt FA = FG, und damit LB ~ B3, also
L ∼B
B
Qualitative Argumentationen sind Abschätzungen, die helfen, eine Situation besser zu
verstehen.
2. Messen, Einheiten
a) Größen und Zahlenwerte
Die natürliche Wahrnehmung ist unvollkommen. Bei technisch-physikalisch nicht vorbelasteten Menschen löst die Vorstellung, daß es Dinge gibt, die unsere Sinne nicht wahrnehmen,
häufig Angstgefühle aus. So ist ein Grund für die emotionale Ablehnung von Kerntechnik,
daß man radioaktive Strahlen nicht sieht. In der Physik lernt man, daß tatsächlich nur ein verschwindender Bruchteil der Wirklichkeit durch unsere Sinne wahrgenommen wird: Dem Auge ist im Spektrum nur ein ein kleiner Bereich zugänglich. Optische Täuschungen verzerren
die Wirklichkeit. Das Wärmeempfinden ist relativ.
Zur Objektivierung von Aussagen werden physikalische Größen gemessen. Dabei ist eine
Größe ein Produkt von Zahl und Einheit. Die Masse meines Körpers ist z.B mK = 85 kg. Die
Einheit ist [mK] = kg. 85 ist die Maßzahl und sie ergibt sich aus Größe durch Einheit.
85 = mK / kg
9
Verschiedene Einheiten, die ein und dieselbe Eigenschaften messen, werden zu einer Dimension zusammengefaßt. So haben g, kg, Unze, Pfund die Dimension Masse, Meile, Zoll Meter
Die Dimension Länge. Wir benutzen SI - Einheiten, die alle Einheiten auf kg, m, s, A, K,
mol, cd zurückführen. Man benutzt dann Einheit und Dimension synonym. Stellt man in einer graphischen Darstellung Zahlenwerte von Größen dar, ist die Achsenbezeichnung Größe/Dimension. Zum Umrechnen von Einheiten ersetzt man die alten Einheiten durch die neuen, indem man die Umrechnungsbeziehungen in die Gleichung einsetzt, als handele es sich
um algebraische Größen.
Abb. 2: In Graphiken werden Zahlenwerte wiedergegeben. Daher
wählt man für die Beschriftung der Achsen am besten Größe / Einheit.
Beispiel: Umrechnen von 15 km/h in m/s:
Umrechnungsbeziehungen:
1 km = 103m
1 h = 3,6 103 s
also:
3
v = 15 km = 15 1km = 15 10 m 3 = 15 m
h
1h
3, 6 ⋅ 10 s 3, 6 s
b) Zugeschnittene Größengleichung
In der Technik benutzt man häufig Gleichungen, bei denen man Zahlenwerte für bestimmte
Einheiten rechts einsetzt und Zahlenwerte für andere Einheiten links erhält. Solche Gleichungen nennt man zugeschnittene Größengleichungen.
Beispiel:
v = 3, 6 ⋅ l , wenn [l] = m, [t] = s und [v] = km/h.
t
Koeffizienten wie hier die 3,6 sorgen dafür, daß die Gleichung trotz der unterschiedlichen
Einheiten richtige Ergebnisse liefert. Einem Physiker sind derartige Koeffizienten, die als
Zahlenwerte erscheinen suspekt. Er vermeidet sie daher nach Möglichkeit.
c) Grundeinheiten im SI - System
Das SI - System (Systeme International) führt alle Einheiten auf die 7 Grundeinheiten kg, m,
s, A (Ampere, zur Messung der elektrischen Stromstärke), K (Kelvin, zur Messung der Temperatur), cd (Candela, zur Messung der Helligkeit) und mol (zur Messung der Stoffmenge)
10
zurück. Die Grundeinheiten werden durch Meßvorschriften festgelegt. Das Kilogramm und
das Meter waren ursprünglich die Masse eines Probekörpers, des Urkilogramms, bzw der
Abstand zweier Markierungen auf einem anderen Probekörper, dem Urmeter. Die Körper
wurden so hergestellt, daß man darauf vertraute , daß sie ihre Eigenschaften beibehalten.
Verbesserungen in der Meßtechnik führen dazu, daß Definitionen der Grundgrößen verändert
werden. So legt man heute das Meter damit fest, daß man der Lichtgeschwindigkeit einen bestimmten Wert zuordnet (etwa 3 108 m/s ) und sagt, 1 m ist die Entfernung die das Licht im
Vakuum in 1/3·10-8 s zurücklegt. 1 s kann sehr genau über die Schwingungszeit einer bestimmten Linie des Cäsiumisotops Cs133 bestimmt werden. Die Messung erfolgt praktisch in
einer Atomuhr. Die zurückgelegte Strecke kann über die Resonanz in Hohlräumen sehr genau bestimmt werden. Generell kann man sagen, daß die Grundeinheiten verläßlicher werden, wenn es gelingt, sie an atomare Eigenschaften anzuknüpfen. So kann man sich vorstellen, daß 1 A dadurch definiert wird, daß bei einer Stromstärke von einem Ampere die Ladung 1Coulomb in einer Sekunde durch einen Leiterquerschnitt transportiert wird. 1 Coulomb wäre dann die Ladung die durch einen Überschuß von einer bestimmten Anzahl von
Protonen oder elektrisch gleichwertigen Teilchen erzeugt wird. Heute wird 1A über die
Kraftwirkung zwischen zwei stromführenden Leitern definiert. Bei unseren Betrachtungen
benötigen wir die genauen Definitionen der Grundgrößen nicht. Die Definition der Temperatureinheit werden wir im Teil "Wärmelehre" kennenlernen. 1 mol können wir uns als die
Stoffmenge vorstellen, die eine ganz bestimmte Anzahl von Teilchen enthält. Die Helligkeit
von Licht werden wir an die Einheit der Leistung in der Mechanik anknüpfen, die mit den
mechanischen Grundeinheiten kg, m, s definiert werden kann.
Die Anforderungen an die Genauigkeit der Grundeinheiten sind im Laufe der Zeit kontinuierlich gestiegen. Während Heinrich I von England noch eine Elle über seine Armlänge festlegte, benötigt man heute für viele Zwecke eine Genauigkeit von 10 signifikanten Ziffern bei
der Festlegung einer Längeneinheit.
Oft wurden in der Physik Fortschritte dadurch erzeugt, daß Messungen für extreme Größen
entwickelt wurden, die bis dahin einer Messung nicht zugänglich waren. Man sollte sich daher klar machen, wie solche extremen Werte gemessen werden, etwa Längen im astronomischen oder mikroskopischen Maßstab, Zeiten im Femtosekundenbereich oder in geologischen Zeiträumen.
3. Bemerkungen zu Fehlern
11
Es gibt keine Messung ohne Fehler. Man unterscheidet absolute Fehler ∆x einer Meßgröße x
und relative Fehler ∆x/x. Ein absoluter Fehler ∆x = 2 mm kann eine sehr hohe Genauigkeit
bedeuten, etwa bei der Bestimmung des Abstandes zwischen Erde und Mond oder eine sehr
geringe Genauigkeit bei der Bestimmung der Größe einer Zelle. Selbst wenn der Stand der
Technik eingehalten wurde und systematische Fehler vermieden wurden, bleiben zufällige
Fehler. D.h. , wenn man eine Messung mehrmals hintereinander mit genügender Genauigkeit
ausführt, ergibt jede Einzelmessung im allgemeinen einen etwas unterschiedlichen Wert xi.
Trägt man die Anzahl der Messungen N(xi), die zu dem gleichen Wert xi führen gegen xi auf,
ergibt sich bei zufälligen Fehlern eine Gaußverteilung oder Normalverteilung.
N(x) = Ce −∆x
Hierin ist
2 /2s 2
C eine Konstante,
∆x die Abweichung des Meßwertes vom Mittelwert
x 1 + x 2 + ... + x n Σ i=1 x i
= n der Mittelwert,
n
1
(x i − x) 2 die Standardabweichung,
s=
n−1 Σ
∆s = s der Fehler des Mittelwertes.
n
s gibt die Breite der Verteilung an. Bei Verteilungen von Größen aus einer Gruppe unteri=n
x=
schiedlicher Objekte, etwa der Körpergröße einer Gruppe von Menschen, bleibt s unabhängig von der Anzahl der Messungen. Bei mehreren Messungen an einem Objekt gibt der Mittelwert das eigentliche Resultat an, und der Fehler des Mittelwertes ∆x wird um so kleiner, je
mehr Messungen man durchführt. Die Gaußverteilung wird im Teil "Wärmelehre" abgeleitet.
Die Behandlung von Fehlern wird in der Physik kultiviert. Geben Sie keinen Zahlenwert in
Ziffern an, die nicht signifikant sind, da zu viele Ziffern eine zu hohe Genauigkeit vortäuschen und die Angabe falsch machen. Man schreibt daher in der Physik Zahlenangaben, besonders von sehr großen oder sehr kleinen Zahlen, als Zahl mit Komma hinter der ersten Ziffer und Zehnerpotenz.
12
KAPITEL B
Kinematik
Die Kinematik befaßt sich mit der Beschreibung einer Bewegung, die im allgemeinen Fall
sehr kompliziert sein kann. Man beschreibt eine solche Bewegung durch Koordinaten oder
Parameter in Abhängigkeit von der Zeit, etwa die Bewegung eines Punktes im dreidimensionalen Raum durch die kartesischen Koordinaten x(t), y(t), z(t), die Bewegung eines ausgedehnten starren Körpers durch die Lage des Schwerpunktes im Raum und durch Winkel, die
seine Drehung angeben. Die Anzahl der unabhängigen Koordinaten, die zur Beschreibung einer Bewegung notwendig sind, nennt man die Zahl der Freiheitsgrade. Wir betrachten zunächst die Bewegung von Teilchen, d.h. alle Effekte, die mit der Ausdehnung eines Körpers
zusammenhängen, werden auf später verschoben. Ein Teilchen hat maximal drei Freiheitsgrade. Zunächst interessiert uns der Zusammenhang von Weg - Zeit - Gesetz, Geschwindigkeit und Beschleunigung.
1. Die geradlinige Bewegung
a) Geschwindigkeit als Ableitung
Wenn das Teilchen sich nur auf einer Geraden bewegen kann, wird die Bewegung durch die
Angabe der Position in Abhängigkeit von der Zeit, d.h. durch das Weg - Zeit - Gesetz x(t)
beschrieben. x kann positive oder negative Werte annehmen. Bei konstanter Geschwindigkeit
ist x(t) eine Gerade und v ist die Steigung der Geraden. Wenn man den Zeitnullpunkt so
wählt, daß bei ihm x = 0 ist, sind Weg und Zeit sogar proportional und
v=
x(t)
t
Abb. 3: Das Weg - Zeit - Gesetz bei konstanter Geschwindigkeit
Auch v kann positive und negative Werte annehmen. Bei einer beschleunigten Bewegung ist
x(t) im allgemeinen eine gekrümmte Kurve.
13
v =
x(t 2 ) − x(t 1 )
t2 − t1
Abb. 4: Das Weg - Zeit - Gesetz bei beschleunigter Bewegung
nennt man die mittlere Geschwindigkeit zwischen den Zeiten t1 und t2.
Beachte: Die mittlere Geschwindigkeit einer sinusförmigen Funktion bei Mittelung über ganze Perioden ist Null.
Die Momentangeschwindigkeit, d.h. die Geschwindigkeit zu einem bestimmten Zeitpunkt, ist
der Grenzwert, den man erhält, wenn man die mittlere Geschwindigkeit in der Umgebung
des betrachteten Zeitpunktes ausrechnet und den Grenzwert für verschwindende Zeitintervalle bildet:
•
v(t) = lim ∆x = dx =x (t)
dt
∆t→0 ∆t
Abb. 5: Das Geschwindigkeits - Zeit - Gesetz bei
beschleunigter Bewegung
v(t) ist die Steigung der Kurve x(t) an der Stelle t. Im allgemeinen gilt nicht v = x/t. Wenn
•
x(t) numerisch gegeben ist, kann x (t) durch die mittlere Geschwindigkeit für kleine Zeitin•
tervalle angenähert werden.  v ≈ ∆x/∆t  . In der Physik ist die Benutzung von ∆x/∆t statt x
für kleine Zeitintervalle ∆t legitim, da der Grenzübergang ∆t →0 oft physikalisch nicht sinnvoll ist, wenn z. B. Abstände kleiner werden als atomare Abstände. Ist die Funktion x(t) ana•
lytisch gegeben, liefert die Mathematik einen Ausdruck für x (t) .
Beispiel:
x = t2
•
x(t 2 ) − x(t 1 )
x = dx = lim ∆x = lim
dt ∆t→0 ∆t ∆t→0 t 2 − t 1
mit t 2 − t 1 = ∆t , also t 2 = t 1 + ∆t wird
14
2
2
2
2
2
∆x = (t 1 + ∆t) − t 1 = t 1 + 2∆tt 1 + ∆t − t 1 = 2t + ∆t
1
∆t
∆t
∆t
daraus folgt
lim ∆x = 2t 1
∆t
∆t→0
dy
statt y / (x) , denn
dx
α) Die unabhängige Variable, nach der abgeleitet wird, ist zu erkennen. Dies ist wichtig,
In der Physik schreibt man gerne
da man es in der Physik meist mit mehrere unabhängigen Variablen zu tun hat.
β) Die Dimension der durch die Ableitung entstehenden Größe ist zu erkennen:
 dx   x  [x]
 =  y  =
[y]
 dy 
dy ∆y
γ)Die Schreibweise suggeriert einen Näherungsausdruck für y/ (x):
≈
dx ∆x
b) Differenziationsregeln
Ähnlich wie oben für die Funktion y = t2 kann man durch Grenzwertbildung für eine Reihe
von Funktionen Ausdrücke für die Ableitung finden. Im folgenden werden die Ableitungen
für einige elementare Funktionen angegeben.
Ausgangsfunktion
differenzierte Funktion
sinx
cosx
(x im Bogenmaß: x/x° = 2π/360°)
cosx
-sinx
x2
2x
(1/2)ax2
ax
xn
nxn-1
const
0
ex (e = 2,718...)
ex
Durch einige Rechenregeln lassen sich Funktionen, die aus den elementaren Funktionen zusammengesetzt sind differezieren:
Rechenregeln:
15
Linearität:
wenn x = x 1 (t) + x 2 (t)
Beispiel: x(t) = x 1 (t) + c
folgt
Produktregel: wenn x(t) = x 1 (t) • x 2 (t)
Beispiel: x(t) = cx 1 (t)
Kettenregel:
•
x (t) = x 1 (t)
→
folgt
→
dx = c dx 1
dt
dt
wenn x = x 1 (x 2 (t))
Beispiel: x(t) = sin ω t
dx = dx 1 + dx 2
dt
dt
dt
dx = dx 1 x + x dx 2
2
1
dt
dt
dt
dx = dx 1 • dx 2
dt dx 2 dt
•
x (t) = ω cos ω t
folgt
→
Die Linearität besagt physikalisch, daß sich bei der Überlagerung zweier Bewegungen die
Geschwindigkeiten addieren, also, wenn ich in einem Fahrzeug sitze, das mit einer Geschwindigkeit von 80 km/h fährt, und mich jemand überholt, wobei seine Geschwindigkeit
von meinem Fahrzeug aus gemessen 40 km/h beträgt, hat er eine Geschwindigkeit von 120
km/h. In der Relativitätstheorie gilt die lineare Überlagerung der Geschwindigkeiten nicht
mehr.
Beschleunigung
Die mittlere Beschleunigung im Zeitintervall ∆t ist die Geschwindigkeitsänderung in dieser
Zeit geteilt durch ∆t:
−
a = ∆v
∆t
Die Momentanbeschleunigung ist
2
•
a = dv = v = d 2x = d  d x 
dt
dt dt
dt
d ist ein Operator. Ein Operator gibt eine Rechenvorschrift an, die auf den dahinter stehendt
den Ausdruck angewandt werden soll. Der Operator muß als Einheit betrachtet werden, in
der z.B. die Größen über und unter dem Bruchstrich nicht gekürzt werden dürfen.
c) Beispiel: die harmonische Schwingung
Betrachte die Projektion s eines mit konstanter Drehzahl rotierenden Punktes.
Nach Abb. 6 gilt
16
s = sin α.
R
Abb. 6: Die harmonische Schwingung kann als die Bewegung aufgefaßt werden, die die Projektion einer Kreisbewegung ausführt.
Der Drehwinkel α (im Bogenmaß gemessen) soll proportional zur Zeit anwachsen
α=ωt
Das Weg - Zeit - Gesetz der Projektion lautet also
s = R sin ω t
Die Konstante ω nennt man die Winkelgeschwindigkeit. Den Zusammenhang von Winkelgeschwindigkeit und Umlaufperiode findet man, indem man in der Gleichung, mit der ω definiert wurde, die Werte für eine Umdrehung einsetzt:
α = 2π,
t=T
T ist die Zeit für einen Umlauf, die Periode. Damit wird die Winkelgeschwindigkeit
ω = 2π
T
s hat sein Maximum, wenn sinωt = 1 ist. Dann ist also s = |R|. s0 = | R| nennt man die Amplitude. Das Weg - Zeit - Gesetz hat also die Form
s = s 0 sin ω t
Die Geschwindigkeit ergibt sich dann durch Differenziation
•
v = s = ω s 0 cos ω t =v 0 cos ω t
17
In der obigen Formel wurde die Größe vor dem Kosinus, d.h. die Amplitude der Geschwindigkeit mit v0 = ωs0 abgekürzt. Die Beschleunigung ergibt sich durch nochmalige
Differenziation
Abb. 7: Der Ort (oben), die Geschwindigkeit (Mitte) und
die Beschleunigung (unten) in Abhängigkeit von der Zeit bei
der harmonischen Bewegung.
•
a = v = −ω 2 s 0 sin ω t = a 0 sin ω
Die Amplitude der Beschleunigung ist also a0 = -ω2s0. Durch Vergleich des Beschleunigungs
- Zeit - Gesetzes und des Weg - Zeit - Gesetzes erkennt man, daß s(t) und a(t) bis auf den
konstanten Faktor -ω2s0 den gleichen Verlauf haben (s. Abb. 7):
a = -ω2s.
d) Die Ermittlung des Weg - Zeit - Gesetzes durch Integration
Im vorigen Abschnitt wurde gezeigt, wie man aus einem bekannten Weg - Zeit - Gesetz x(t)
die Geschwindigkeit und die Beschleunigung ermittelt. Im folgenden Abschnitt geht es um
die umgekehrte Aufgabe: v(t) sei bekannt und x(t) soll ermittelt werden. Diese Umkehroperation muß bei einer der Grundaufgaben der Mechanik bewältigt werden: bei bekannten
Kräften auf einen Körper, seine Bewegung auszurechnen. Da F = ma, ist primär a bekannt
und aus a muß v(t) und schließlich x(t) bestimmt werden.
Wenn v konstant ist, gilt x = v0t. x ist geometrisch die Fläche des durch v und t aufgespannten Rechtecks (Abb. 8 oben). Wenn v nicht konstant ist, teilt man die Gesamtzeit in Zeitintervalle ∆t ein, die so klein sind, daß sich innerhalb von ∆t v genügend wenig ändert. Für jedes
Teilintervall gilt ∆xi = vi∆t. ∆xi entspricht dem schraffierten Flächenstück unter der v(t) -
18
Kurve (Abb. 8 unten). Der gesamte zurückgelegte Weg ist geometrisch durch die Fläche gegeben, die
durch v(t), die t - Achse und durch die Parallelen zur v - Achse durch t1 und t2 begrenzt wird.
Man schreibt
Abb. 8: Bei konstanter Geschwindigkeit ist s = vt (oben). Daher ist
bei variabler Geschwindigkeit s die Fläche unter der Kurve v(t).
Σv i (t)∆t = ∫ t v(t)dt
∆t→0
t2
x = lim
1
Die Integration ist die Umkehrung der Differenziation. Man kann also die "Stammfunktion"
x(t) aus der Tabelle der Differenziationsformeln ablesen. Dabei ist zu beachten, daß die
•
Stammfunktion nicht eindeutig bestimmbar ist. Wenn v = at
ist v = a . Aber, wenn v =
•
at + c, ist ebenfalls v = a , da d c = 0. Die Integralfunktion ist also nur bis auf eine unbedt
stimmte Konstante bekannt. Sie heißt deshalb unbestimmtes Integral. Die additive Konstante
bestimmt man aus den Anfangsbedingungen. Das bestimmte Integral ist eine Zahl. Sie ergibt
sich aus:
t2
∫ t v(t)dt = [x(t)] t
t2
1
= x(t 2 ) − x(t 1 )
x(t) (wir schreiben im folgenden auch häufig s(t) ) ist die Stammfunktion von v(t). Analog
gilt
v = ∫ a(t)dt
Die wichtigsten Formeln für die Kinematik der geradlinigen Bewegung lauten also:
19
2
v = ds , a = dv = d 2s
dt
dt
s(t) = ∫v(t)dt, v(t) = ∫ a(t)dt
e) Geradlinige Bewegung mit konstanter Beschleunigung
Es soll vorausgesetzt werden:
a = const und zur Zeit t = 0 sei v = v0 und s = s0.
Dann ist
v = ∫ adt = at + c 1
Durch Einsetzen der Anfangsbedingung für v ergibt sich
v0 = a ⋅ 0 + c1,
also
v0 = c1
v = at+v 0
Durch nochmaliges Integrieren ergibt sich
s = ∫vdt = ∫ (at + v 0 )dt = 1 at 2 +v 0 t + c 2
2
Durch Einsetzen der Anfangsbedingung für s erhält man die Konstante s2
s 0 = 1 a ⋅ 0 2 +v 0 ⋅ 0 + c 2 ,
2
c2 = s0
Das Weg - Zeit - Gesetz lautet damit
s = 1 at 2 +v 0 t + s 0
2
Sonderfälle
α) Freier Fall
Hier ist a = g. g ist die Erdbeschleunigung. v0 und s0 sollen zur Zeit t = 0 verschwinden. Dann
ist der beim Fall zurückgelegte Weg
s = 1 gt 2
2
20
und die Geschwindigkeit nach der Zeit t
v = gt
β) Bremsvorgang
Hier wird für eine Abschätzung a ebenfallsals konstant angesehen. Der Zahlenwert ist negativ. Das hat allerdings auf die formelmäßige Ausrechnung keinerlei Auswirkung. Die Anfangsgeschwindigkeit ist jetzt ungleich Null v = v0. Der Bremsweg wird von dem Ort an gemessen, an dem sich das Fahrzeug zur Zeit t = 0 befand: s0 = 0. Das Weg - Zeit - Gesetz
heißt also:
s = 1 at 2 + v 0 t
2
Das Geschwindigkeits - Zeit - Gesetz
v = at+v 0 t
Die Bremszeit ergibt sich aus der Bedingung v(tB) = 0
v
t B = − a0
und mit dieser Zeit der zurückgelegte Weg aus dem Weg - Zeit - Gesetz
v 20
v 20
v0
1
1
s B = a 2 −v 0 a = − a
2 a
2
Als Anwendung wird die Bremsverzögerung ausgerechnet, die bei der Faustformel aus der
Fahrschule vorausgesetzt wird:
2
2
3
2
sB  v0
 =  v 0 ⋅ 3, 6 ⋅ 10 s  =v 2 3, 6 s 2
=
0
m  km/h ⋅ 10 
 10 3 m ⋅ 10 
100 m 2
Vergleich mit der Formel für den Bremsweg ergibt
−2a = 1002 m2
3, 6 s
→
a = −3, 86 m2
s
21
2. Die krummlinige Bewegung von Teilchen
a) Vektoren
α) Vektoren als Zahlentripel
Zur Beschreibung der Bewegung eines Teilchens in drei Dimensionen gibt man seine drei
Koordinaten, z.B. die Projektionen seines Aufenthaltsortes auf die drei kartesischen Achsen
an: x(t), y(t), z(t) (s. Abb. 9). Zur Vereinfachung sagt man, die Position ist gegeben durch
den Ortsvektor x.
 x(t)
x(t) =  y(t)

 z(t)





Allgemein ist
 ax 
a =  a y 


 az 
ax, ay, az sind die Komponenten von a. a enthält die Information über den Abstand des Punktes vom Koordinatenursprung. Dies ist der Betrag des Vektors
a = a = a 2x + a 2y + a 2z ,
und die Richtung der Verbindungslinie zwischen Koordinatenursprung und der Position des
Punktes. Man kann daher einen Vektor geometrisch als Pfeil darstellen, dessen Schwanz im
Koordinatenursprung ruht, während seine Spitze auf den betrachteten Punkt zeigt. Alle physikalischen Größen, für die die Angabe der Richtung wichtig ist, wie s, v, a, F, B werden
durch Vektoren dargestellt.
 v x (t)
v(t) =  v y (t)

 v z (t)

,



 Fx 
F =  F y 


 Fz 
Alle übrigen wie Masse, Energie, Zeit nennt man Skalare.
22
Abb. 9: Die Länge eines Vektors im dreidimensionalen Raum.
b) Einige Operationen mit Vektoren
Die Vektorschreibweise kürzt ab. Es bedeutet:
a + b = c:
ax + bx = cx
ay +by = cy
az +bz = cz
b = αa:
(α soll ein Skalar sein)
bx = αax
by = αay
bz = αaz
•
v =x
vx = x
•
vy = y
•
vz = z
x(t) = ∫ v(t)dt
x = ∫ v x (t)dt
y = ∫ v y (t)dt
z = ∫ v z (t)dt
•
Es gibt verschiedene Produkte zwischen Vektoren, die bestimmten Erfordernissen in der
Physik angepaßt sind (s. Abschnitt e).
c) Realisierung von Vektoraddition: Überlagerung von Bewegungen
Bewegt sich ein Fahrzeug mit x0(t) auf einer Straße und beschreibt man die Bewegung eines
Körpers auf dem Fahrzeug relativ zum Fahrzeug mit xrel(t), so ist die Gesamtbewegung des
Körpers von der Straße aus gesehen (s. Abb. 10)
23
Abb. 10: Überlagerung von Bewegungen,
erklärt am eindimensionalen Fall.
xges(t) =x0(t) + xrel(t)
Durch Differentiation erhält man
vges(t) = v0(t) + vrel(t)
ages(t) = a0(t) + arel(t)
Geschwindigkeiten und Beschleunigungen addieren sich zur Gesamtgeschwindigkeit bzw.
zur Gesamtbeschleunigung. Die Überlagerung von zweidimensionalen Bewegungen ist in
Abb. 11 dargestellt. Danach gilt hier:
Abb. 11: Addition von Bewegungen in der Ebene.
xges(t) = x0(t) + xrel(t)
yges(t) = y0(t) + yrel(t)
usw.
d.h.
xges(t) = x0(t) + xrel(t)
vges(t) = v0(t) + vrel(t)
ages(t) = a0(t) + a rel(t)
Geometrisch erhält man also die Vektoraddition, indem man durch Parallelverschiebung einen der Vektoren mit seinem Schwanz an den Kopf des anderen hängt. Der Summenvektor
24
ist dann der Pfeil zwischen Schwanz und Kopf des gesamten Gebildes (Abb. 12). Diese Konstruktion ist mit der Parallelogrammkonstruktion äquivalent. Der Differenzvektor ist der
Pfeil zwischen den Spitzen der Ausgangsvektoren (Abb. 13).
Abb. 12: Vektoraddition nach der Kopf - an Schwanz - Methode
Abb. 13: Die Differenz zweier Vektoren
d) Die Geschwindigkeit bei krummliniger Bewegung
Die Definition der Geschwindigkeit, wie sie oben vorgenommen wurde, weicht von dem Geschwindigkeitsbegriff, wie er im täglichen Leben verwendet wird, ab. In der Physik benötigt
man zur Charakterisierung der Geschwindigkeit eines Körpers im Raum drei Zahlen. Im täglichen Leben begnügt man sich mit einer Zahl, etwa der Anzeige des Tachometers im Auto.
Von der physikalischen Definition her ist dies der Betrag des Geschwindigkeitsvektors. Man
sagt auch die Bahngeschwindigkeit. Um uns den Zusammenhang zwischen dem Vektor der
Geschwindigkeit und seinem Betrag zu veranschaulichen, stellen wir uns vor, wir wollten die
Bahngeschwindigkeit eines Fisches, der in einem Aquarium auf einer gekrümmten Bahn
schwimmt, messen. Dazu nehmen wir mit drei Videokameras, die senkrecht auf drei Außenflächen des Aquariums ausgerichtet sind, den Fisch in gleichen Zeitabständen ∆t auf. In dieser Zeit ändert sich die Position in den drei Koordinatenrichtungen um ∆x, ∆y und ∆z. Der
Geschwindigkeitsvektor ist also


v =


∆x
∆t
∆y
∆t
∆z
∆t





Der Betrag der Geschwindigkeit ist durch den Betrag des zurückgelegten Weges
∆x = ∆x 2 + ∆y 2 + ∆z 2
25
geteilt durch ∆t näherungsweise gegeben. (Für den genauen Wert muß man den Grenzwert
bilden). Daher ist die Bahngeschwindigkeit näherungsweise
v ≈
∆x
=
∆t
∆x 2 + ∆y 2 + ∆z 2
=
∆t
 ∆x  +  ∆y  +  ∆z 
 ∆t 
 ∆t 
 ∆t 
2
2
2
und exakt nach dem Grenzübergang:
v =
2
2
2
 dx  +  dy  +  dz  = v 2 + v 2 + v 2 = v
x
y
z
 dt 
 dt 
 dt 
Die Bahngeschwindigkeit ist also identisch mit dem Betrag des Geschwindigkeitsvektors.
Entsprechendes gilt für den Betrag der Beschleunigung.
Beachte: Den Vektor der Beschleunigung erhält man aus der Differentiation des Vektors der
Geschwindigkeit, aber den Betrag der Beschleunigung erhält man im allgemeinen Fall nicht
aus Differentiation des Betrages der Geschwindigkeit.
Dies wird in den unten durchgerechneten Beispielen von krummlinigen Bewegungen (der
Kreisbewegung und dem waagerechten Wurf) deutlicher. Man kann es aber jetzt schon anschaulich einsehen. Bei einer Kreibewegung, die mit konstanter Bahngeschwindigkeit verläuft, ändert sich der Betrag der Geschwindigkeit definitionsgemäß nicht. Die Richtung der
Geschwindigkeit ändert sich aber ununterbrochen. Der Geschwindigkeitsvektor ist also
zeitabhängig und der Beschleunigungsvektor ungleich Null. Der Grund dafür, daß man in der
Physik einen anderen Geschwindigkeits- und Beschleunigungsbegriff als im täglichen Leben
benutzt, liegt daran, daß man damit die Dynamik einheitlicher formulieren kann.
Mit der Vektorschreibweise können wir jetzt Geschwindigkeit und Beschleunigung allgemein definieren:
v(t) = lim
∆x(t) dx(t)
=
∆t
dt
a(t) = lim
∆v(t) dv(t)
=
∆t
dt
∆t→0
∆t→0
Beispiel für die Überlagerung von Geschwindigkeiten:
26
Ein Windsurfer fahre mit der konstanten Geschwindigkeit v0. Der Wind habe die Geschwindigkeit vwind, von einem ruhenden Bezugssystem aus gemessen. Welche Richtung und welche
Stärke hat der Wind, vom Surfer aus gesehen?
Abb. 14: Windverhältnisse beim Segeln.
Die Verhältnisse sind in Abb. 14 dargestellt. Durch Vergleich mit der Betrachtung in Abb.
11 identifizieren wir vwind mit vges, und die Windgeschwindigkeit vom Surfer aus gesehen mit
vrel. Die quantitative Bestimmung würde über die Berechnung des Dreiecks der Geschwindigkeitsvektoren erfolgen, also z.B. nach dem Kosinussatz
v 2rel = v 2wind + v 20 − 2v wind v 0 cos α
e) Produkte von Vektoren
α) Das Skalarprodukt
Das Skalarprodukt ist definiert durch
a • b = ab cos α
wobei α der Winkel zwischen a und b ist. Bei der Verknüpfung der beiden Vektoren entsteht
ein Skalar. Das Skalarprodukt läßt sich aus den Komponenten der Einzelvektoren ermitteln.
Dazu stellen wir a und b in der kartesischen Basis ex, ey, ez dar (Abb. 15).
Abb. 15: Die Basisvektoren eines kartesischen Koordinatensystems.
1 
e x =  0  ,
 
0 
0 
e y =  1  ,
 
0 
0 
e z =  0 
 
1 
27
 ax 
1 
0 
0 






a =  a y  = a x  0  + a y  1  + a z  0  = a x e x + a y e y + a z e z
 
 
 


0 
0 
1 
 az 
In dieser Darstellung werden a und b multipliziert.
a • b = (a x e x + a y e y + a z e z ) • (b x e x + b y e y + b z e z )
Die Klammern werden wie gewohnt ausmultipliziert, wobei man beachtet, daß für i ≠ k , da
es sich um eine kartesische Basis handeln soll, α = 90°, cosα = 0 und daher e i •e k = 0 , für
i = k hingegen α = 0, cosα = 1, e i • e i = 1 gilt. Man erhält
a • b = axbx + ayby + azbz
Anwendungen des skalaren Produktes
i. Ermittlung des Winkels zwischen zwei Vektoren, die durch ihre Komponenten gegeben
sind.
Da a • b = ab cos α erhält man cos α =
axbx + ayby + azbz
a 2x + a 2y + a 2z
b 2x + b 2y + b 2z
ii. Arbeit, wenn F und s nicht parallel sind (Abb. 16).
Abb. 16: Das skalare Produkt erzeugt die Projektion eines
Vektors auf eine vorgegebene Richtung.
W = F s ⋅ s = Fs cos α = F • s
iii. Kosinussatz (Abb. 17)
Abb. 17: Der Kosinussatz ist mit dem Skalarprodukt leicht zu
beweisen.
c=a-b
28
c2 = (a - b)·(a - b) = a2 + b2 - 2a·b = a2 + b2 - 2 ab cosα
β) Das Vektorprodukt
Das Vektorprodukt ordnet zwei Ausgangsvektoren einem Produktvektor zu nach folgender
Vorschrift:
a × b = c.
heißt
c = ab sinα
Abb. 18: Die Korkenzieherregel legt die Richtung des Produktvektors im Vektorprodukt fest.
c steht senkrecht auf a und b
a, b und c bilden eine Rechtsschraube.
Die erste Bedingung legt den Betrag des Produktvektors fest, die zweite die Richtung, wobei
das Vorzeichen noch offen bleibt, das dann durch die dritte Bedingung geregelt wird. Diese
wird in Abb. 18 erläutert. Man legt den Griff eines Korkenziehers in Richtung des ersten
Vektors, hier a, dreht diesen auf dem kürzesten Weg so, daß er parallel zum zweiten Vektor
liegt. Der Korkenzieher schraubt sich dann - vorausgesetzt er ist nicht speziell als Sylvesterscherz mit Linksgewinde ausgestattet - in Richtung des Produktvektors.
Um die Komponentendarstellung des Vektorproduktes zu erhalten, verfahren wir wie oben
beim skalaren Produkt. Die Einzelvektoren werden in einer kartesischen Basis dargestellt
unddas Vektorprodukt gebildet:
a × b = (a x e x + a y e y + a z e z ) × (b x e x + b y e y + b z e z )
Berücksichtigt man jetzt, daß laut Definition des Vekterproduktes
e i × e k = 0 für i = k
und
29
ex × ey = ez
ey × ez = ex
ez × ex = ey
sowie die Tatsache, daß aufgrund der Korkenzieherregel das Produkt das Vorzeichen umkehrt, wenn die Reihenfolge der Faktoren umgekehrt wird, so erhält man
 aybz − azby
a × b =  a z b x − a x b z

 axby − aybx





x, y, z werden in jeder Zeile zyklisch vertauscht. Man kann die Komponentendarstellung formal gewinnen, indem man eine Determinante aus den drei Baisvektoren und den Ausgangsvektoren des Vektorproduktes bildet.
ex ax bx
a × b = ey ay by
ez az bz
Anwendungen des Vektorproduktes
i. Flächeninhalt eines Parallelogrammes
Abb. 19: Der Flächeninhalt eines Parallelogramms
ist durch Grundlinie mal Höhe gegeben.
Nach Abb. 19 ist die Fläche A gegeben durch
A = a·h = absinα
Nach der Definition des Vektorproduktes kann man also schreiben
A= a×b
Häufig ordnet man in der Physik einer Fläche einen Vektor A zu, dessen Betrag gleich dem
Flächeninhalt der Fläche ist und der senkrecht auf der Fläche steht. Dann gilt für den Vektor
der Fläche, die durch die Vetoren a und b aufgespannt wird
30
A=a×b
ii. Anwendungen aus der Physik
wir werden im Verlaufe dieses Grundkurses eine Reihe von weiteren Anwendungen des
Vektorproduktes kennenlernen. Die wichtigsten sind
das Drehmoment
M=r×F
der Drehimpuls
L=r×p
und die Lorentzkraft
F = Qv × B
f) Beispiele für krummlinige Bewegungen
α) Der waagerechte Wurf
Setzt man voraus, daß ein Fallversuch, den man in einem Wagen ausführt, der sich mit konstanter Geschwindigkeit geradlinig bewegt, gleich ausfällt, wie ein Fallversuch in einem ruhenden System - vernachlässigbarer Luftwiderstand sei vorausgesetzt - so sieht ein ruhender
Beobachter den im Wagen durchgeführten Fallversuch als waagerechten Wurf. Der waagerechte Wurf kann also aufgefaßt werden als Überlagerung einer horizontalen Bewegung mit
konstanter Geschwindigkeit - der Bewegung des Wagens - und eines freien Falles. Das
Experiment zeigt, daß bei waagerechtem Wurf der Boden gleich schnell erreicht wird wie bei
freiem Fall aus gleicher Höhe. Die beiden Bewegungen überlagern sich also ungestört. Bei
einer solchen ungestörten Überlagerung sagt man auch, das Galileische Relativitätsprinzip
gilt. Die horizontale Bewegung wird also dargestellt durch
Abb. 20: Der waagerechte Wurf kann als Überlagerung einer
geradlinigen, gleichförmigen waagerechten Bewegung mit
dem freien Fall aufgefaßt werden.
vx = v0
x = v0t
31
die vertikale durch
vy = gt
y = (1/2)gt2
Der Ortsvektor
 v0t 
x(t) =  1 2 
 2 gt 
ist die Bahnkurve in Parameterdarstellung, d.h., wenn man für t irgend welche positiven Zahlen einsetzt, erhält man für x Punkte der Bahnkurve. Die Bahn in kartesischen Koordinaten
folgt hieraus durch Elimination von t.
t = vx
0
also
g
y = 1 2 x2
2 v0
v 
v= 0 
 gt 
v = v 20 + (gt)
2
Die Wurfbahn ist eine Parabel.
β) Die gleichförmige Kreisbewegung
Ein Punkt bewege sich mit konstanter Bahngeschwindigkeit auf einem Kreis. Die geometrischen Verhältnisse sind in Abb. 21 dargestellt. Der Drehwinkel wächst proportional mit der
Zeit.
Abb. 21: Die geometrischen Verhältnisse bei der gleichförmigen Kreisbewegung.
α=ωt
32
•
ω ist konstant, daher gilt α = ω und ω gibt die Geschwindigkeit an, mit der α wächst. ω
wird daher Winkelgeschwindigkeit genannt. Der Zusammenhang mit der Umlaufszeit T ist
wie bei der Schwingung
ω = 2π = 2πf
T
f ist die Anzahl der Umläufe pro Sekunde, d.h. die Umlauffrequenz oder Drehzahl. Die zurückgelegte Strecke s ist die Bogenlänge. Um diese auf den Drehwinkel α zurückzuführen,
beachten wir, daß s proportional zu α ist: s = cα. Bei einer Umdrehung ist α = 2π und s =
2πR. Daher gilt
s = αR
•
•
s =α R
•
Mit α = ω erhält man
v = ωR
Da ω und R konstant sind, ist auch v konstant. Der Geschwindigkeitsvektor v ist nicht konstant, da er stetig seine Richtung ändert. ∆v und damit a ≈ ∆v zeigt, wie an Abb. 21 zu er∆t
kennen ist - zumindest im Grenzübergang - zum Kreismittelpunkt.
s
Aus ∆v
v = R , ∆v = a∆t und s =∆t folgt
a∆t = v∆t
v
RT
2
a = v = ω2R
R
und damit
Die Bewegung ist also beschleunigt, obwohl die Bahngeschwindigkeit v konstant ist.
Die oben durch geometrische Betrachtungen gewonnenen Ausdrücke für die Geschwindigkeit und die Beschleunigung bei der Kreisbewegung lassen sich ganz formal durch Differentiation des vektoriellen Weg - Zeit - Gesetzes finden. Nach Abb. 22 ist
x = R cos α
33
y = R sin α
Mit α = ωt sind also die Komponenten des Ortsvektors des bewegten Punktes gegeben durch
Abb. 22: Die Koordinaten des Ortsvektors r
x = R cos ωt
y = R sin ωt
Der Ortsvektor schreibt sich
 R cos ωt 
r=

 R sin ωt 
2
Sein Betrg ist
r = R 2 cos 2 ωt + R 2 sin 2 ωt =R (cos 2 α + sin α = 1).
Differentiation der Komponenten ergibt
•
v x = x = −Rω sin ωt
•
v y = y = Rω cos ωt
Der Geschwindigkeitsvektor ist
 −sin ωt 
v = Rω 
 cos ωt 
Sein Betrag
v = v 2x + v 2y = Rω
r • v = R 2 ω(−sin ωt cos ωt + cos ωt sin ωt) = 0
v steht also senkrecht auf r. Die Beschleunigung ergibt sich durch Ableitung der Komponenten des Geschwindigkeitsvektors.
•
a x = v x = −Rω 2 cos ωt
•
a y = v y = −Rω 2 sin ωt
 cos ωt 
a = −Rω 2 

 sin ωt 
34
a = a 2 = Rω 2
Durch Vergleich der Formeln für r und a erhält man
a = −ω 2 r
Der Vektor der Beschleunigung ist also zu jeder Zeit entgegengesetzt zum Ortsvektor gerichtet. Er zeigt also auf den Mittelpunkt des Kreises.
Abb. 23: Die Hintereinanderausführung zweier Drehungen ist nicht vertauschbar.
γ) Ergänzung: Die Winkelgeschwindigkeit als Vektor.
Zur Charakterisierung der Winkelgeschwindigkeit ist eine Richtung notwendig, nämlich die
Richtung der Drehachse, und ein Betrag. Es liegt daher nahe, auch der Winkelgeschwindigkeit einen Vektor zuzuordnen. Versucht man zunächst die Drehung um einen endlichen Winkel als Vektor aufzufassen, wobei die Hintereinanderausführung zweier Drehungen analog
zu der Hintereinanderausführung zweier Verschiebungen der Addition der Vektoren entspricht, so erleidet man Schiffbruch. Wie Abb. 23 zeigt, hängt das Ergebnis von der Reihenfolge der Operationen ab. Dahingegen sind infinitesimale Drehungen dα Vektoren (s. Abb.
24), da sie in einem Körper lineare Verschiebungen erzeugen, und diese sind durch Vektoren
darstellbar.
Abb. 24: Eine infinitesimale Drehung führt zu einer
infinitesimalen Verschiebung sämtlicher Punkte im
Körper. Diese haben Vektorcharakter.
35
dα
Vektorcharakter. Man definiert ω so, daß der
dt
Vektor parallel zur Drehachse ausgerichtet ist und mit der Drehrichtung eine Rechtsschraube
Da dα Vektorcharakter hat, hat auch ω =
bildet (Abb. 25). Außerdem ist ω = ω. Mit Dieser Definition kann man jetzt den Zusammenhang zwischen v und r bei der Kreisbewegung auch vektoriell schreiben.
Abb. 25: Die Winkelgeschwindigkeit als Vektor
Betrachte Abb. 25. Aus v = Rω folgt mit R = r sinγ v = rω sinγ. Da v senkrecht zu r und ω,
und ω, r, v eine Rechtsschraube bilden, kann man schreiben
v=ω×r
Der Ortsvektor r hat seinen Ursprung auf der Drehachse.
Für die Beschleunigung erhält man, wenn ω konstant ist
a = dv = ω × dr = ω × v = ω × (ω × r)
dt
dt
Abb. 26: Die Vektoren r, v, a bei der gleichförmigen
Kreisbewegung.
δ) Der schiefe Wurf
i. Die Bahn
Auch der schiefe Wurf kann als Überlagerung einer waagerechten, gleichförmigen Bewegung und einer senkrechten Bewegung mit konstanter Beschleunigung aufgefaßt werden. Als
Unterschied zum waagerechten Wurf gibt es eine senkrechte Anfangsgeschwindigkeit.
36
Abb. 27: Die Bahn beim schiefen Wurf.
v x (0) =v 0x = v 0 cos α
v y (0) =v 0y = v 0 sinα
Die Geschwindigkeit ist jetzt also gegeben durch
v x = v 0 cos α
v y = v 0 sin α − gt
und damit die Koordinaten des Wurfkörpers
x = v 0 t cos α
y = v 0 t sin α − 1 gt 2
2
Dabei wurden als Anfangsbedingungen vorausgesetzt, daß bei t = 0 auch x = 0 und y = 0 sein
sollen. Die Bahnkurve in kartesischen Koordinaten ergibt sich dann durch Elimination von t.
x
t = v cos
α eingesetzt
0
2
g
sin α
y = cos α x − 1 2 x 2
2 v cos α
(1)
Die Bahnkurve ist wie beim waagerechten Wurf eine Parabel, allerdings liegt jetzt der Scheitelpunkt der Parabel nicht im Abwurfpunkt.
ii. Bestimmung der Wurfhöhe
Die Wurfhöhe ist das Maximum der Wurfparabel. Man erhält es durch die Bedingung
dy dy dx
dy/dx = 0. Wegen der Kettenregel
und der Bedingung dx ≠ 0 ist dies gleichbe=
dt dx dt
dt
deutend mit vy = 0, wie anschaulich sofort zu verstehen ist.
Aus vy(tmax) = 0 folgt
v y = v 0 sin α − gt max = 0
→ t max =
v o sin α
g
37
Einsetzen in y(t) ergibt
h=
v 20 sin 2 α 1 v 20 sin 2 α v 20
−
=
sin 2 α
g
g
2
2g
iii. Bestimmung der Wurfweite xw
Abwurfhöhe und Auftreffhöhe sollen gleich sein. Aus Gleichung (1) ergibt sich dann für y =
0.
gx w
sin α
cos α x w − 2v 2 cos 2 α = 0
2
2 sin α cos α =
gx w
v2
Abb. 28: Eine bestimmte Wurfweite kann man mit zwei Abwurfwinkeln erreichen.
v2
x w = g0 sin 2α
Die maximale Wurfweite erhält man für sin2α = 1, d.h. αmax = 45°.
v 20
x w max = g
Vergleich mit h zeigt, daß sie doppelt so groß ist wie die maximal erreichbare Höhe. Wenn
die Wurfweite vorgegeben ist, ergeben sich für α ≠ 45 zwei Winkel mit α2 = 90 - α1. Wenn
x und y des Auftreffpunktes vorgegeben sind, läßt sich der Abwurfwinkel aus der Bahngleichung berechnen.
cos 2 α =
a ± a 2 − bc
2c
mit a = 1 - y/2h, b = (x/2h)2, c = 1 + (y/x)2, 2h = v02/g
38
h ist die Wurfhöhe bei senkrechtem Wurf bei gleichem v0.
g) Approximation von Kurven
α) Die Taylorentwicklung
Die Taylorentwicklung ermöglicht die Beschreibung des Verlaufs einer Kurve in der Umgebung eines Anfangspunktes, indem nur ihre Eigenschaften in diesem Anfangspunkt ausgenutzt werden. Betrachte z.B. die Preisentwicklung im Laufe der Zeit P(t) (Abb. 29).
Abb. 29: Preisanstieg und Änderung der Preisanstiegsrate.
Nullte Näherung
Man nimmt an, die Preise bleiben konstant P = P(t0).
Erste Näherung
Die Preise erhöhen sich gemäß der augenblicklichen Preissteigerungsrate
P = P(t 0 ) +  dP  (t − t 0 )
dt t
P = P 0 + P / (t 0 )∆t
Zweite Näherung
Die Änderung der Preissteigerungsrate wird mit einem quadratischen Ansatz berücksichtigt:
P = a 0 + a 1 ∆t + a 2 ∆t 2
Man bestimmt die Konstanten a0, a1 und a2 so, daß die ursprüngliche Funktion P(t) und das
Polynom für ∆t = 0 in der nullten, ersten und zweiten Ableitung übereinstimmen.
Nullte Ableitung: P(∆t) = a0 +a1∆t + a2∆t2. Aus ∆t = 0 folgt a0 = P(t0).
Erste Ableitung: P/(t) = a1 + 2a2∆t. Aus ∆t = 0 folgt a1 = P/(t0).
zweite Ableitung: P//(t) = 2a2. Aus ∆t = 0 folgt a2 = (1/2)P//(t0)
39
Die zweite Näherung lautet also:
P = P 0 + P / (t 0 )∆t + 1 P // (t 0 )(∆t) 2
2
Im Prinzip kann man so fortfahren. Diese Entwicklung heißt Taylorentwicklung. Mit ihr läßt
sich bei bekannten Ableitungen am Punkt t = t0 der weitere Verlauf einer analytischen Funktion beliebig genau vorhersagen. Die Approximation ist um so besser, je kleiner ∆t ist. In der
Physik begnügt man sich in den allermeisten Fällen mit der Entwicklung bis zur ersten Ordnung. Die zweite Ordnung wird dann allenfalls zur Abschätzung des Fehlers verwendet.
Abb. 30: Die Tangente der Kurve r(t) ist durch ihre Ableitung gegeben.
β) Approximation von Raumkurven (Bogenlänge, Krümmung und Torsion)
Eine Raumkurve sei durch eine Parameterdarstellung r(t) gegeben. Einige Formeln werden
besonders übersichtlich, wenn man als Parameter die Bogenlänge s der Kurve vom Anfangspunkt aus wählt. Die Bogenlänge ergibt sich aus
v = ds = v 2x + v 2y + v 2z
dt
•2
•2
•2
s = ∫ x +y +z dt
i. Lineare Näherung
In erster Näherung wird die Kurve r(t) durch die Tangente beschrieben. Die Richtung der
•
Tangente ist gegeben durch v = r . Der Tangenteneinheitsvektor ist daher e t = dr 1v . Mit
dt
ds
dr
dt
dr
⋅ =
v =
erhält man e t =
dt ds ds
dt
40
e t = dr
ds
•
Manchmal ist es bequemer mit e t = vr zu rechnen.
ii. Quadratische Näherung
Für die quadratische Näherung sucht man den Kreis, dessen erste und zweite Ableitung im
Berührungspunkt mit den entsprechenden Ableitungen der Kurve gleich ist. Dieser Kreis
heißt Schmiegungskreis. Sein Radius R ist der Krümmungsradius der Kurve, κ = 1/R ist die
Krümmung. Jede Bewegung auf einer gekrümmten Bahn läßt sich in der Umgebung eines
Punktes durch eine Kreisbewegung annähern. In einer ebenen Bewegung liegt der Krümmungskreis in der Bewegungsebene. Zur Angabe der Ausrichtung des Schmiegungskreises
in einer allgemeinen Bewegung benötigt man den Normalen Einheitsvektor. Er steht senkrecht auf dem Tangentenvektor und in der Ebene des Schmiegungskreises. Um ihn aus der
gegebenen Raumkurve zu berechnen, betrachten wir die Beschleunigung, wobei v(t) mit Hilfe des Tangenten Einheitsvektors dargestellt wird, der selbst zeitabhängig ist.
v = v(t) ⋅ e t (t)
dv = dv e +v de t = dv e + v 2 de t
t
t
dt
ds
dt dt
dt
(2)
a setzt sich zusammen aus der Tangentialbeschleunigung
a t = dv e t
dt
und der Normalbeschleunigung
a n =v 2
de t
ds
Die Bewegung verläuft also in der Ebene, die durch at und an aufgespannt wird. Dies ist definitionsgemäß die Schmiegungsebene. Bei der gleichförmigen Kreisbewegung ist at = 0 und
de
an = v2/R. Die obige allgemeine Formel ergibt für at = 0 a n = v 2 t . Durch Vergleich erhält
ds
man
41
d 2 r(s)
de t
=
=1
2
R
ds
ds
Die zweite Ableitung des Ortsvektors nach der Bogenlänge ergibt die Krümmung der Kurve.
de t
Der Vektor
liegt also, da er proportinal zur Normalbeschleunigung ist, senkrecht zur
ds
Tangente der Kurve und außerdem in der Schmiegungsebene. Der Normaleneinheitsvektor
ist damit
en = R
de t
ds
et, en, und e b = e t × e n bilden eine rechtwinklige Basis, die im Punkte r(t) an die Kurve geheftet ist. Bei Durchlaufen des Parameters t läuft die Basis an der Kurve entlang und ändert im
allgemeinen die Richtung seiner Achsen. Diese Basis nennt man das begleitende Dreibein. eb
3
ist der Binormalenvektor. d r gibt ein Maß für die Torsion. Eine ebene Kurve hat die Torsi3
on Null.
42
KAPITEL C
Dynamik von Massenpunkten
1. Die Newtonschen Axiome
a) Newtons Formulierung der Axiome
Die Dynamik soll die Bewegung eines Körpers aus den Kräften, die auf den Körper wirken
"erklären", d.h. auf Axiome zurückführen. Ein Axiomensystem soll in sich widerspruchsfrei,
vollständig und frei von überflüssigen Annahmen sein. Im Grunde beruht das Axiomensystem
der klassischen (nichtrelativistischen) Mechanik auf den von Isaak Newton (1643 -1727) ausgesprochenen Prinzipien. In vereinfachter Form sind dies:
Das Trägheitsprinzip
Ein kräftefreier Körper bewegt sich gleichförmig, geradlinig.
Das Aktionsprinzip
Wirkt auf einen Körper eine Kraft F, so erhält er eine Beschleunigung a = F/m.
Das Reaktionsprinzip
Übt ein Körper A auf B eine Kraft F aus, so übt B auf A eine Kraft -F aus.
b) Das Trägheitsprinzip
Das Trägheitsprinzip widerspricht in vieler Hinsicht menschlicher Erfahrung: Ein nicht gezogener Wagen kommt zum Stillstand. Das Trägheitsprinzip wurde zuerst von Galileo Galilei
(1564 - 1624) formuliert. Galileis Vorstellungen zur Mechanik entwickelten sich an den Bemühungen, die Widersprüche in der bis dahin geltenden Bewegungslehre des Aristoteles (384
- 322 v. Chr., Schüler Platons und Lehrer Alexander des Großen) und seiner Nachfolger
(Scholastiker, Peripatetiker) zu vermeiden. Nach Aristoteles fallen z.B. schwere Körper
schneller als leichte. Ein leichter Körper müßte also eigentlich einen schwereren bremsen. Andererseits müßte das Gesamtsystem aus leichtem und schwerem Körper schneller als die Einzelkörper fallen, da es ja insgesamt schwerer als jeder einzelne Teil ist. Galilei versuchte
durch genaue Experimente seine Aussagen zu belegen. Um die Meßgenauigkeit zu erhöhen Zeiten wurden durch ausfließende Wassermengen gemessen - untersuchte Galilei später statt
des freien Falls die Bewegung auf einer schiefen Ebene. Er fand als erster experimentell die
Gesetze der gleichförmig beschleunigten Bewegung und formulierte sie mathematisch. Die
Popularität verdankt Galilei seinen astronomischen Entdeckungen (Mondkrater, Jupitermonde) und dem Inquisitionsprozeß der katholischen Kirche gegen ihn.
43
Abb. 31: Eine Kugel rollt um so
weiter, je weniger die rechte Ebene geneigt ist, im Grenzfall gegen
unendlich, wenn Reibung vernachlässigt werden kann.
Das Trägheitsgesetz begründete Galilei mit einem Gedankenexperiment (Abb. 31): Eine Kugel rolle eine schiefe Ebene herunter, und nachdem sie unten angekommen ist, an der anderen
Seite mit ihrem Schwung eine schiefe Ebene hinauf. Ohne Reibung würde die Kugel bis zur
Ausgangshöhe hinaufrollen. Gibt man nun der zweiten schiefen Ebene unterschiedliche Neigungen, so würde im Grenzfall der Neigung Null die Kugel bis ins Unendliche laufen. Ähnlich wie bei einer schiefen Ebene erreicht auch bei einem reibungsfreien Pendel die Kugel die
Ausgangshöhe, auch wenn man das Pendel bei der Bewegung verkürzt wie beim Galileischen
Pendel (Abb. 32).
Abb. 32: Das Fadenpendel erreicht die ursprüngliche Höhe,
auch wenn ein Hindernis in den Weg des Fadens geschoben
wird.
c) Das Aktionsprinzip
α) Definition einer Kraftskala
Das Aktionsprinzip wurde von Newton formuliert. Es führt gegenüber der Kinematik zwei
neue Größen ein: die Masse und die Kraft. Newton stellt sich die Masse als eine dem Volumen proportionale Stoffeigenschaft vor. In heutiger Sprechweise würde man sagen, die Masse
ist proportional der Anzahl Protonen und Neutronen. Um genauer zu sein muß man eine Massenskala definieren. Man kann z.B. mit ein und derselben Kraft mit verschiedenen Massen Beschleunigungsversuche machen. Eine Kraftskala ergibt sich dann aus Beschleunigungsversuchen mit einer Masse und verschiedenen Kräften. Wenn a und m festgelegt sind, definiert das
Aktionsgesetz die Kraft. Die Definition der Kraft über die Beschleunigung kann leicht zu dem
Mißverständnis führen, daß in einer statischen Situation keine Kräfte vorhanden sind. Dies ist
aber nicht richtig. Zwar verschwindet dann die Summe aller Kräfte auf einen Körper, aber es
kann innere Kräfte in einem Körper geben, die z.B. bei Festigkeitsbetrachtungen eine Rolle
spielen. Ein anderes Beispiel ist ein Magnetvertschluß.
44
Das Aktionsgesetz
F = ma
legt die Dimension der Kraft fest: [F] = [m] [a] =kgm/s2 . Hierfür gilt die Abkürzung N (Newton). Ein Newton ist die Kraft, die notwendig ist, einen Körper der Masse 1kg die Beschleunigung 1m/s2 zu erteilen. Ein Körper der Masse 1kg wird im Erdfeld an der Erdoberfläche im
freien Fall um 9,81 m/s2 beschleunigt, d.h. auf 1kg wirkt die Gravitationskraft von 9,81 N.
Wenn die Kräfte, die auf einen Körper wirken, und seine Masse bekannt sind, kann man das
Aktionsgesetz benutzen, um die Beschleunigung zu ermitteln und daraus durch zweimalige Integration die Bewegung r(t) abzuleiten. Dies ist eine der Grundaufgaben der Dynamik.
Beispiele:
Schiefer Wurf:
Fx = 0, also ax = 0.
Fy = -gm, also ay = -g.
Die weitere Rechnung wurde oben in der Kinematik vorgeführt.
Kreisbewegung:
a = Rω2 = v2/R
Die Kreisbewegung wird durch eine Kraft F = mRω2, die auf den Kreismittelpunkt gerichtet
ist, erzwungen (Zentripetalkraft).
β) Zerlegung von Kräften
Da Kräfte durch F = ma definiert sind, haben sie wie a Vektorcharakter. Man kann daher eine
Kraft als Summe mehrerer Kräfte auffassen (Kraftzerlegung) oder mehrere Kräfte zu einer resultierenden zusammenfassen. Dabei gilt die bei Vektoren eingeführte Dreiecks -, bzw.
Parallelogrammkonstruktion.
Beispiel:
Schiefe Ebene (s. Abb. 33)
Welche Gesamtkraft beschleunigt den Körper auf der schiefen Ebene? Lösung: Zerlege die
Gewichtskraft FG in eine Tangentialkomponente Ft und eine Normalkomponente Fn. Fn wird
durch die Kraft, die durch die Auflage auf den Körper ausgeübt wird, kompensiert. Die
45
Abb. 33: Kräftezerlegung an der schiefen Ebene
Ft = FG sinα
Fn = FGcosα
Abb. 34: Kräftezerlegung beim Fadenpendel
resultierende Kraft ist Ft. Die gleiche Zerlegung gilt für das Fadenpendel. Der Faden übt eine
Kraft aus, die die Richtung des Fadens besitzt (Abb. 34).
Daß die Kraft entlang eines gewichtslosen Fadens überall gleich ist, erleichtert manchmal die
Lösung dynamischer Probleme. Betrachte das Beispiel von Abb. 35 . Hier gilt
Ma = F1
mg - F2= ma
F1 = F2
daraus folgt
und
mg - Ma = ma
mg
a=
M+m
a=g 1M
1+
Abb. 35: Hier wird über den Faden eine zusätzliche Kraft zu
der Schwerkraft ausgeübt
46
d) Das Reaktionsprinzip
α) Begründung des Reaktionsprinzips
Das Reaktionsprinzip besagt, daß Kräfte zwischen Körpern immer in entgegengesetzt gleichen
Paaren auftreten. Man spricht daher in der Physik anstatt von Kräften häufig von Wechselwirkungen. Das Reaktionsprinzip zeigt die Erfahrung. Heute würde man es am deutlichsten mit
der Unmöglichkeit eines Perpetuum Mobile begründen (s. Abb. 36).
Abb. 36: Würde das Reaktionsprinzip nicht gelten, müßte
sich das Gebilde von zwei Massen von selbst in Rotation
versetzen.
Bringt man zwei Körper m1 und m2, von denen m1 auf m2 die Kraft F21 und m2 auf m1 die
Kraft F12 ausübt, am Umfang eines Rades an, so würde dieses einen Antrieb erfahren, wenn
F12 ungleich -F21 wäre.
Die Angriffspunkte der entgegengesetzten Kräfte liegen im allgemeinen an unterschiedlichen
Stellen. Bei Körpern, die auf einer Unterlage liegen, wird die Schwerkraft von der elastischen
Kraft der Unterlage kompensiert.
β) Definition des Impulses
Betrachtet man zwei Körper mit den Massen m1 und m2, zwischen denen eine Kraft wirkt
(Abb. 37), so gilt
Abb. 37: Zur Definition des Impulses
•
F 12 = m 1 v 1 ,
•
und F 21 = m 2 v 2
•
•
•
•
wegen F12 = - F21 folgt daraus m 1 v 1 = −m 2 v 2 , d.h. m 1 v 1 + m 2 v 2 = 0 und daher
m 1 v 1 + m 2 v 2 = const.
Physikalische Größen, die bei bestimmten Prozessen konstant bleiben, sind angenehm für die
Beschreibung von Vorgängen. Man nennt sie Erhaltungsgrößen. Man definiert daher
47
mv = p
p ist der Impus eines Körpers (englisch momentum). Bei mehreren Körpern ist
pges = m1 v1 + m2 v2 + ... = Σmi vi
der Gesamtimpuls. Der Gesamtimpuls ist die vektorielle Summe der Einzelimpulse. Das Aktionsgesetz schreibt sich dann
•
F= p
γ) Der Impulssatz
Aus dem im vorigen Abschnitt gesagten folgt sofort, daß der Gesamtimpuls von Körpern, die
nur inneren Kräften ausgesetzt sind, konstant bleibt. In der klassischen Mechanik ist der Impulssatz äquivalent mit dem Reaktionsprinzip. In der relativistischen Mechanik zeigt sich, daß
das Reaktionsprinzip nicht mehr gilt, während der Impulssatz nicht angetastet wird. Nach einem Satz von Emmy Nöther (1882 - 1935) ist der Impulssatz eine Folge der Tatsache, daß der
Raum homogen ist, d.h. daß Experimente an verschiedenen Stellen des Raumes gleich
ausfallen.
Beispiele:
In Antriebssystemen von Raketen, Flugzeugen und Schiffen wird Masse nach hinten ausgestoßen. Da der Gesamtimpuls - bei Vernachlässigung der Reibung - konstant bleiben muß, resultiert ein Antrieb des Fahrzeuges. Bei Hochheben eines Gewichtes wird die Erde - wenigstens
im Prinzip - beschleunigt. Die Impulserhaltung wird mit Personen auf Rollbrettern demonstriert, die aufeinander Kräfte ausüben.
e) Historische Randbemerkungen
Im 16. Jahrhundert wurde die Physik in drei Richtungen erweitert:
Die Bedeutung des quantitativen Experimentes wurde erkannt.
Man erkannte, daß die auf der Erde gültige Physik auch am Himmel gilt.
Die Begriffe von Masse und Kraft kristallisierten sich heraus.
Aus heutiger Sicht muß man sagen, daß die Newtonschen Axiome weder vollständig noch minimal sind. Das erste folgt aus dem zweiten. Der besondere Hinweis des ersten Axioms ist historisch verständlich. Wie man aus relativistischen Effekten weiß, enthält Newtons Mechanik
48
die nicht korrekte Annahme vom absoluten Raum und absoluter Zeit, d.h. man setzt voraus,
daß unabhängig von Körpern ein fundamentales Bezugssystem und eine Uhrzeit definiert werden können, die für alle anderen Bezugssysteme gilt. Da dies nicht möglich ist, wird es
schwierig, ein "Inertialsystem" anzugeben, d.h. ein Koordinatensystem, in dem sich ein kräftefreier Körper ohne Beschleunigung bewegt. Auf der Erde gibt es nur in gewisser Näherung
ein Inertialsystem, da die Erde um ihre eigene Achse rotiert und eine Umlaufbahn um die Sonne vollführt. Auch die Sonne bewegt sich im Milchstraßensystem auf einer gekrümmten Bahn.
2. Kräfte
a) Die Grundkräfte
Um die Bewegung aus der Wirkung der Kräfte berechnen zu können, benötigt man genauere
Angaben über die Kräfte. Die verschiedenen in der Natur auftretenden Kräfte lassen sich auf
wenige Grundkräfte zwischen Elementarteilchen zurückführen.
Gravitation (Massenanziehung)
elektrostatische Kraft (Kraft zwischen ruhenden Ladungen)
magnetische Kraft (zusätzliche Kraft zwischen bewegten Ladungen)
starke Wechselwirkung (Kräfte zwischen Quarks)
schwache Wechselwiorkung (Kraft zwischen Neutrinos)
Nach heutigem Wissen können die elektrostatische, die elektromagnetische und die schwache
Kraft als verschiedene Erscheinungsformen einer Kraft verstanden werden. Dies leistet die
"vereinheitlichte Theorie". Alle diese Kräfte sind Fernkräfte in dem Sinne, daß keine Berührung zwischen Oberflächen von wechselwirkenden Körpern stattfindet. Zwischen den Elementarteilchen sind in jedem Fall, auch wenn wir nicht den Eindruck haben, riesige Zwischenräume. Die im täglichen Leben vorkommenden Kräfte lassen sich entweder auf Gravitation
oder - wie bei Reibung, Elastizität, Kräften durch chemische Prozesse oder Wärme - auf elektromagnetische Kräfte zurückführen. Scheinkräfte wie die Corioliskraft oder die Zentrifugalkraft muß man in Rechnung stellen, wenn man eine Bewegung in einem beschleunigten Bezugssystem beschreibt. Im unbeschleunigtem System, also einem Inertialsystem, sind Scheinkräfte überflüssig.
49
b) Die Gravitation
α) Historische Vorbemerkungen
An der Erdoberfläche ist die Gravitationskraft FG = mger. Newton bemerkte, daß ein waagerechter Wurf mit zunehmender Anfangsgeschwindigkeit stetig in eine Umlaufbahn um die Erde übergeht (Abb. 38).
Abb. 38: Wie man einen waagerechten Wurf in eine Planetenbahn überführen kann.
Umgekehrt kann man eine Umlaufbahn etwa des Mondes um die Erde lokal als Näherung einer Wurfparabel betrachten. Aus der kinematisch bekannten Wurfparabel ergibt sich die Erdanziehung im Abstand des Mondbahnradius von der Erde. Diese kann man nun vergleichen
mit der bekannten Erdanziehung an der Erdoberfläche und so eine Aussage über die Abhängigkeit der Erdanziehung in Abhängigkeit vom Abstand des Körpers vom Erdmittelpunkt erhalten. Wir gehen diesen Weg im folgenden nicht, sondern einen etwas eleganteren, indem wir
die Erdanziehung der Zentripetalkraft mrω2 gleichsetzen. Das Ergebnis ist das gleiche wie wie
bei einem Vergleich mit der Wurfparabel. Die Abhängigkeit der Kraft vom Abstand der Massen ergibt sich dann aus Keplers dritten Gesetz, das die Halbachsen der Bahnellipsen der Planeten mit ihrer Umlaufszeit T verknüpft. In der Näherung von Kreisbahnen mit dem Radius r
3
besagt das Keplersche Gesetz: r 2 = const und damit r 3 ω 2 = const für alle Planeten. Setzt man
T
voraus, daß die Zentripetalkraft von der Massenanziehung herrührt, die eine Funktion des Abstandes zwischen Sonne und Planeten ist, also die Form |F| = f(r) besitzt, so gilt für zwei
Planeten
m 1 r 1 ω 21 = f(r 1 )
m 2 r 2 ω 22 = f(r 2 )
Rechnet man ω auf die Umlaufszeit T um und dividiert beide Gleichungen, so erhält man
T 21
T
2
=
m 1 r 1 f(r 2 )
m 2 r 2 f(r 1 )
50
Das 3. Keplersche Gesetz ist nur erfüllt, wenn
f(r) ∼ m2
r
d.h. wenn
f(r 1 ) =
m1c
m c
und f(r 2 ) = 22 .
2
r
r
β) Das Gravitationsgesetz
Abb. 39: Zwei Massen im Abstand r ziehen sich an.
Wir verallgemeinern die Anziehung zwischen Sonne und Planeten auf die Anziehung zweier
beliebiger Körper mit den Massen m1 und m2 (Abb. 39). Vorläufig sehen wir von speziellen
Effekten, die durch die Ausdehnung der Körper hervorgerufen werden ab, d.h. wir stellen uns
die Körper als kleine Kugeln vor. Wegen der Symmetrie der Anordnung nehmen wir an, daß
die Anziehungskraft F zwischen den Körpern beiden Massen proportional ist. Wir schreiben
daher für den Betrag der Kraft
F=γ
m1m2
r2
(1)
und vektoriell
F = −γ
m1m2 r
r2 r
Die Proportionalitätskonstante γ nennt man die Gravitätskonstante. Für sie ergibt sich experimentell der Wert γ = 6,67 10−11 Nm2/kg2 (s. nächsten Abschnitt). Aus Gleichung (1) folgt für
einen Körper an der Erdoberfläche (r = RE)
und damit g = γ M2
mg = γ mM
2
R
R
(RE : Radius der Erde, M: Masse der Erde, m: Masse des Körpers) Wenn γ bekannt ist, läßt
sich also aus den bekannten Größen Erdbeschleunigung g und Radius der Erde RE die Masse
der Erde bestimmen.
51
In Laborexperimenten rechnet man gewöhnlich mit einer konstanten Erdanziehung. Um den
relativen Fehler zu bestimmen, den man macht, wenn man für g den Wert an der Erdoberfläche nimmt, obwohl man sich in einer Höhe h befindet, entwickelt man F(r) in der Umgebung
von r = RE in einer Taylorreihe.
F(h) =
γmM
(R E + h)
2
=
γmM
R 2E
1
1 + h 
RE 

2
df
Für die Funktion f(∆x) = (1 + ∆x)n ergibt die Taylorentwicklung f(∆x) ≈ f(0) +  
∆x
 dx  ∆ =
df
= n erhhält man (1 + ∆x)n ~ 1 + n∆x. Mit
mit f(0) = 1 und f/(∆x) = n(1 + ∆x)n - 1, also  
 dx  ∆x=0
∆x = h/RE und n = 2 ergibt sich schließlich
F(h) =
γmM 
1−2 h 
2 
RE 
R
Der prozentuale Fehler ist also 2h/RE.
γ) Messung der Gravitationskonstanten
Abb. 40: Gravitationswaage nach Cavendish.
Die Massen M können auf die andere Seite der
Massen m herumgeschwenkt werden.
Die Gravitationskonstante kann durch Messungen im Labor bestimmt werden. Dies erfolgte
erstmals durch Cavendish 1787 (Henry Cavendish 1731 - 1810). Zwei Massen m hängen an
einem Torsionsfaden, dessen Verdrehung über einen Spiegel empfindlich gemessen werden
kann (Abb. 40). Bringt man zur Zeit t = 0 zwei Massen M in die Nähe der aufgehängten Massen, so fangen diese aufgrund der gegenseitigen Anziehungskraft an, sich zu bewegen. Aus
der Beschleunigung dieser Bewegung und aus der neuen Ruhelage ergibt sich γ.
52
c) Kraft zwischen ausgedehnten Körpern
α) Integration über Massenelemente
Bei ausgedehnten Körpern muß über die Kräfte zwischen allen Einzelteilchen summiert werden. Für die Kraft zwischen einem punktförmigen Teilchen der Masse mp und einer homogenen Kugel ergibt sich (s. Abb.41)
Abb. 41: Um die Kraft auf einen homogenen Körper auszurechnen, muß im allgemeinen Fall integriert werden.
F ≈ γm p Σ
∆m i r i
r2 ri
Nach dem Grenzübergang
F = γm p ∫ r3 dm
r
dm = ρdxdydz
r = r p − s = (x p − x) + (y p − y) + (z p − z)
2
2
2
Die Integration ist nach geeigneter Transformation durchführbar (s. z.B. Alonso - Finn BdI,
Kap. 13.7). Es ergibt sich der Satz: Homogene Kugeln haben im Außenraum die gleiche Gravitationswirkung wie ein Massenpunkt der gleichen Masse im Mittelpunkt der Kugel. Vorsicht: Dieser Satz gilt für Kugeln. Für Körper mit anderen Formen gilt er im allgemeinen
nicht, auch wenn man den Mittelpunkt durch den Schwerpunkt ersetzt, wie man sofort am
Beispiel des Ringes erkennt. Würde nämlich ein Ring durch einen Massenpunkt im Scherpunkt, der im Mittelpunkt des Ringes liegt, zu ersetzen sein, ergäbe sich auf einen anderen
Körper, der sich im Schwerpunkt befindet, eine unendliche Kraft
F =lim γ
r→0
mM R
2
In Wirklichkeit heben sich die Kräfte, die alle Teilelemente des Ringes auf eine Masse im
Mittelpunkt ausüben, gegenseitig auf. Es gibt eine sehr elegante Möglichkeit, zu beweisen,
daß eine Kugel im Außenraum die gleichen Anziehungskräfte hat wie ein Massenpunkt im
53
Zentrum. Zu diesem Zweck symmetrisiert man das Problem, indem man nicht die Wechselwirkung zwischen zwei Massen betrachtet, sondern die Veränderung des Raumes, die durch
eine Masse in ihrer Umgebung hervorgerufen wird. Diese Veränderung nennt man Feld.
β) Feldstärke
Die Kraft in der Umgebung einer Masse M hängt von M aber auch von der Probemasse mp ab,
auf der diese Kraft ausgeübt wird. Um eine von der Probemasse unabhängige Größe zu erhalten, definiert man die Feldstärke G des Gravitationsfeldes:
G = mF = −γ M2 rr
p
Jedem Punkt in der Umgebung der Masse M ist also ein Feldstärkevektor zugeordnet. Man
sagt, in der Umgebung der Masse M existiert ein Feld, in diesem Fall ein kugelsymmetrisches
Feld. G hat die gleiche Richtung wie F. Man erhält die Kraft, die im Feld G auf eine Masse m
ausgeübt wird aus
F = mG
γ) Der Fluß
Wir stellen uns jetzt eine strömende Flüssigkeit vor. An jedem Ort in einem gewissen Raum
hat die Flüssigkeit eine lokale Geschwindigkeit v(r). Es liegt also ein Geschwindigkeitsfeld
vor. Als Fluß durch die Fläche A bezeichnet man dann das Flüssigkeitsvolumen, das in einer
Zeiteinheit durch A strömt.
Beispiel: Wie hängt der Verkehrsfluß mit der Verkehrsdichte und der Geschwindigkeit der
Fahrzeuge zusammen?
Abb. 42: Die Anzahl der Fahrzeuge (schwarze Punkte),
die in einem Zeitintervall die Kontrollfläche K passieren,
sind alle die, die sich zwischen K und dem letzten Fahrzeug befinden, das K in dem betrachteten Zeitintervall K
N: Gesamtzahl der Wagen, l: Gesamtstrecke, n = N/l: Verkehrsdichte
In der Zeit ∆t fahren alle Fahrzeuge durch die Kontrolle K, die nicht weiter als l = v∆t vom
Kontrollpunkt entfernt sind. Durch die Verkehrsdichte ausgedrückt sind dies ∆N = ln also
∆N = vn∆t Fahrzeuge. Als Fluß ergibt sich also
54
Φ = ∆N = nv
∆t
Abb. 43: Im dreidimensionalen Fall strömt das schaffrierte
Volumen durch die Fläche A.
In einer dreidimensionalen Strömung definiert man als Dichte n = N/V, worin V das Volumen
ist, das N Teilchen enthält. Um alle Teilchen zu erfassen, die durch die Fläche A strömen, muß
man jetzt die Flüssigkeitsmenge betrachten, die in der Zeit ∆t durch A strömt. In Abb. 43 ist
sie schraffiert gezeichnet. Das Volumen dieser Flüssigkeitsmenge ergibt sich aus Grundfläche
A mal Höhe h = l cosα. Die Anzahl der Teilchen, die in der Zeit ∆t durch A strömen ist also
∆N = nV = nAh = nAl cos α = nAv∆t cos α
und der Fluß
∆N = nA • v
∆t
Mit N = nV wird daraus für den Fluß
∆V = A • v
∆t
Man definiert daher für ein beliebiges Vektorfeld v(r) den Fluß des Feldes durch die Fläche A
als Φ = A•v , wenn v über A konstant ist, sonst Φ = ∫ v • dA . Die Bedeutung des Begriffes
Fluß rührt daher, daß der Gesamtfluß, der durch eine Fläche geht, die eine Quelle ganz umschließt, unabhängig von der Form und Größe der Fläche ist. Als Fluß des Gravitationsfeldes
definiert man
Φ = A • G , oder allgemein
Φ = ∫ G • dA
Wir stellen uns dieses Integral als Summe aller Flüsse durch die Flächenelemente ∆Ai vor.
Φ ≈ Σ Gi • Ai
55
δ) Das Gesetz von Gauß
Für eine Punktmasse gilt für den Fluß durch eine Kugeloberfläche mit dem Radius r, in deren
Mittelpunkt die Masse liegt
Φ = A • G = AG = 4πr 2
γM
= 4πγM = const
r2
Der Gesamtfluß ist also unabhängig vom Radius der Fläche. Daraus folgt sofort, wie aus der
Analogie zum Fluß in einem Strömungsfeld mit einer lokalisierten Quelle zu ersehen ist, daß
der Gesamtfluß durch eine geschlossene Fläche, die die Masse umgibt, auch unabhängig von
der Form der Fläche ist, denn im stationären Zustand muß die gesamte Flüssigkeitsmenge, die
die Quelle liefert, auch durch diese Fläche strömen. Die obige Formel für den Gesamtfluß des
Gravitationsfeldes einer Punktmasse gilt aber auch für beliebige Massenverteilungen mit der
Gesamtmasse M. Dies liegt daran, daß sich die Flüsse einzelner Massen linear superponieren,
d.h., daß der Fluß durch ein Flächenelement A von mehreren Massen gleich der Summe der
Flüsse der einzelnen Massen durch dieses Flächenelement ist (Abb. 44).
Abb. 44: Der Fluß des Feldes der einzelnen Massen addiert
sich zum Gesamtfluß.
 m 
m

Φ ges = γ  Σ 3i r i  • A = γ Σ  3i r i • A  = Σ Φ i
 r 
r

Der Fluß durch eine geschlossene Fläche kann durch Summierung der Flüsse durch die
Teilflächen erhalten werden. D.h. der Gesamtfluß durch eine geschlossene Fläche um eine
Masse M, die sich aus Teilmassen mi zusammensetzt: M = m1 + m2 + ... = Σmi ist gleich der
Summe der Flüsse durch diese geschlosene Fläche die von den einzelnen Teilmassen ausgehen. Da der Fluß für jede Teilmasse unabhängig von der Größe und Form der geschlossenen
Fläche ist, gilt das auch für den Gesamtfluß aller Massen und damit für den Fluß von M. Diese
Tatsache wird als Gesetz von Gauß bezeichnet. Wir formulieren es so:
56
Der gesamte Fluß der Gravitationsfeldstärke einer Masse M durch eine geschlossene Fläche,
die M ganz umgibt, ist Φ = 4πγM , unabhängig von der Form und Größe der Fläche.
Der Gesamtfluß kann also sofort angegeben werden.
ε) Beispiele
i. Gravitationsfeld einer ausgedehnten Kugel im Abstand r
Abb. 45: Aus dem Fluß im Abstand r läßt sich bei einer Kugel die Feldstärke des Gravitationsfeldes berechnen.
Der Fluß durch eine konzentrische Kugelfläche mit dem Radius r (wobei r größer als der Kugelradius sein muß) ist nach dem Gesetz von Gauß
Φ = ∫ G • dA = 4πγM
Da aus Symmetriegründen G konstant und G parallel zu A ist, gilt
∫ G • dA = G ⋅ 4πr 2
Daraus folgt G = γ M2 undF = γ mM
2
Für die Kraftwirkung außerhalb einer homogenen Kugel kann diese durch einen Massenpunkt
der Masse M im Mittelpunkt der Kugel ersetzt werden.
ii. Kraft im Innern einer Kugelschale
Abb. 46: Zur Berechnung des Gravitationsfeldes im Innern
einer Kugelschale.
Die Kugelschale ist in Abb. 46 schraffiert gezeichnet. Um die Feldstärke im Innern auszurechnen wird eine Kugelfläche betrachtet, die ganz im Innern der Schale liegt. Wegen der gleichen
57
Symmetrie wie im vorigen Beispiel erhält man das gleiche Ergebnis. Nur umschließt die Kugelfläche in diesem Falle keine Masse, d.h. M = 0. Daraus folgt Φ = 0 und damit G = 0. Im Innern der Kugelschale gibt es keinerlei Gravitationskraft. Während das Ergebnis von Aufgabe
i. oft intuitiv richtig geraten wird, ist das von Aufgabe ii. weit weniger unmittelbar einsichtig.
Mit dem Gesetz von Gauß kann man also Feldstärken und damit auch Kräfte ausrechnen.
Dummerweise funktioniert das Verfahren nur, wenn man, wie in den obigen Beispielen aus
Symmetriegründen von vorneherein sagen kann, daß die Feldstärke - zumindest über bestimmte Raumbereiche - konstant bleibt. In praxi gibt es also nur sehr wenige Situationen, in
denen man das Gaußsche Gesetz zur Berechnung einer Feldstärke wirklich anwenden kann.
Für Abschätzungen und grundsätzliche Betrachtungen ist es aber ein sehr mächtiges
Hilfsmittel.
d) Andere Grundkräfte
α) Die elektrostatische Kraft
Für die Kraft zwischen ruhenden geladenen Teilchen gilt das Coulombgesetz.
F=
Q1Q2 1 r
4πε 0 r 2 r
Die Form ist identisch mit dem Gravitationsgesetz. Daher gelten die Ausführungen, die für
das Gravitationsgesetz gemacht wurden auch für das Coulombgesetz. Q sind Ladungen, die im
Gegensatz zur Masse auch negative Werte annehmen können. Die Dielektrizitätskonstante ε0
ist wie γ eine experimentell zu ermittelnde Konstante
1 = 9 ⋅ 10 9 Nm 2
4πε 0
(As) 2
Die Ladungen von Elementarteilchen sind ganze Vielfache der Elementarladung
e 0 =1, 6 ⋅10 −19 As . Ausnahmen bilden die Quarks mit 1/3 und 2/3 der Elementarladung. Diese
werden aber nicht einzeln beobachtet. Das Gesetz von Gauß heißt in der Elektrostatik
Q
∫ E • dA = ε
E ist die elektrische Feldstärke, die ähnlch wie bei der Gravitation gebildet wird
58
E= F
Qp
F ist die Kraft, die durch das Feld auf die Probeladung ausgeübt wird.
β) Die Lorentzkraft
Bewegte Ladungen erfahren zusätzlich die Lorentzkraft
F = Qv × B
γ) Kernkräfte
In der Kern- und Elementarteilchenphysik spielen außer den bisher behandelten Kräften die
starke und die schwache Wechselwirkung eine Rolle. Es gibt Teilchen wie die Neutrinos, die
nur die schwache Wechselwirkung zeigen. Andere wie die Elektronen zeigen die schwache
und die elektromagnetische Wechselwirkung. Die Quarks zeigen neben diesen beiden Wechselwirkungen die starke Wechselwirkung, die dann alle übrigen Kräfte dominiert. Die starke
Wechselwirkung kann auf eine Größe zurückgeführt werden, die der Ladung in der Elektrostatik analog ist. Man nennt sie Farbladung. Es gibt drei verschiedene Farbladungen und ihre
komplementären Ladungen. Die Quarks streben die Gesamt"farbe" weiß an. Dies ist möglich,
indem sich zwei Quarks mit komplementären Farben verbinden. Man erhält dann Mesonen. Es
ist aber auch möglich, indem sich drei Quarks mit allen drei unterschiedlichen Grundfarben
verbinden. Man erhält dann Baryonen, z.B. Protronen und Neutronen. In der Quantenfeldtheorie benötigt man weitere Teilchen, die für den Quantencharakter bei der Kraftüberttragung
sorgen. Bei der Gravitation sind dies Gravitonen, bei der Elektromagnetik Photonen, bei der
starken Wechselwirkung Gluonen, bei der schwachen Wechselwirkung W und Z Teilchen.
Die Kraftteilchen können selber Kräften ausgesetzt sein wie bei den Gluonen oder neutral erscheinen wie bei den Photonen.
e) Kräfte zwischen makroskopischen Körpern
Bisher wurden Kräfte zwischen einzelnen Körpern betrachtet, von deren Ausdehnung abgesehen wurde. Streng genommen gelten die besprochenen Kraftgesetze für Massenpunkte. In praxi können wir uns darunter die elementaren Teilchen der Materie vorstellen. Die Kräfte zwischen zusammengesetzten Körpern ergeben sich dann durch Addition der Kräfte zwischen allen Elemenarteilchen. Diese Addition ist in den seltensten Fällen wirklich durchführbar. In einigen Fällen gibt es für die Kraft eines zusammengesetzten Körpers einfache Erfahrungssätze.
Diese werden im folgenden besprochen. Sie haben natürlich nicht den fundamentalen
59
Charakter wie die Grundkräfte und deswegen auch nur einenbegrenzten Gültigkeitsbereich.
Typisch für diese makroskopischen Kräfte sind Materialkonstanten, die durch eine übergeordnete Theorie oder experimentell bestimmt werden müssen.
α) Kraft durch elastische Verformung
Abb. 47: Das Spannungs - Dehnungs - Diagramm von
festen Körpern.
Dehnt man einen Körper, etwa einen Draht mit dem Querschnitt A, indem man an beiden Enden eine Kraft F aufwendet, so ergibt sich für die relative Längenänderung dl/l in Abhängigkeit von der angewandten Spannung σ = F/A typischerweise das in Abb.47 dargestellte Verhalten: Bei kleinen Auslenkungen ist die Dehnung der Spannung proportional
σ = F = E dl
A
l
Die Proportionalitätskonstante E nennt man den Elastizitätsmodul. Diese lineare Näherung des
eigentlichen Spannungs/Dehnungs Gesetzes nennt man das Hookesche Gesetz, den Bereich, in
dem es gilt, den Proportionalitätsbereich (in Abb. 47 geht er bis zum Punkt P). Überschreitet
man den Bereich, muß man höhere Glieder der Taylorentwicklung mit berücksichtigen. Ab einer bestimmten Grenze (E) verformt sich ein Körper bleibend. Der Elastizitätsbereich ist überschritten. Bei noch größeren Verformungen fängt der Körper an, zu fließen (F) oder er bricht.
Die Festigkeit eines Körpers ist die Grenzspannung, bei der er reißt. Ähnliche Gesetze wie für
die Dehnung gelten für die Scherung, d.h. die Belastung eines Körpers mit einer Kraft, die
parallel zur belasteten Fläche ausgerichtet ist. Bei der Dehnung einer Spiralfeder wird der
Draht torsionell verformt. Für den Zusammenhang von äußerer Kraft und Längenenderung der
Feder gilt in einem weiten Bereich das Hookesch Gesetz
F = Dx
D ist die Federkonstante, die die Steifigkeit der Feder beschreibt.
60
β) Reibungskraft
i. Reibung zwischen festen Körpern
Abb. 48: Ein fester Körper mit glatter Oberfläche auf einer festen Unterlage.
Bei festen Körpern mit ebenen Grenzflächen ist die Reibungskraft FR parallel zur Berührungsfläche ausgerichtet und der Kraft, die beide Körper aufeinanderdrückt, der sogenannten Normalkraft, proportional (Abb. 48). Bei Grenzflächen zwischen festen Körpern ist FR von der
Flächengröße unabhängig. Der Grund liegt darin, daß nur wenige Auflagepunkte existieren,
deren Anzahl etwa unabhängig von der Flächengröße ist.
F R = µF N
Der Reibungskoeffizient µ wird experimentell bestimmt. Er unterscheidet sich für Haft-,
Gleit-, und Rollreibung. Eine nahezu reibungsfreie Bewegung kann auf einer Luftkissenbahn
realisiert werden. Durch das Wechselspiel von Gleit- und Haftreibung können interessante Bewegungsabläufe resultieren etwa wie bei dem Spielzeug Hackspecht.
Eine einfache Möglichkeit zur Bestimmung des Reibungskoeffizienten besteht darin, einen
Körper auf eine schiefe Ebene zu lege und den Neigungswinkel zu messen, bei dem er anfängt
zu gleiten (dies ergibt den Koeffizienten der Haftreibung), oder bei dem er gerade noch gleitet
(dies ergibt den Koeffizienten der Gleitreibung). Nach Abb. 49 ist
Abb. 49: Bestimmung des Reibungskoeffizienten auf
der schiefen Ebene.
F t = mg sin α
F N = mg cos α
61
Im Grenzfall ist Ft = FR = µFN, also mg·sinα = µmg·cosα und µ = tan α
ii. Reibung in Flüssigkeiten und Gasen
Wir stellen uns zunächst einen Körper in einer mit der Geschwindigkeit v strömenden Flüssigkeit vor, etwa ein Fahrzeug, das sich mit der Geschwindigkeit v in der umgebenden Luft
bewegt. Bei hohen Geschwindigkeiten erzeugen die anströmenden Teilchen die Reibung
durch Stoß auf die Wand. Man erhält dann eine Reibungskraft, die proportional zum Impusverlust aller Teilchen ist. Der Impulsverlust wird ein bestimmter Bruchteil ihres Anfangsimpulses sein. Wenn ∆N Teilchen in der Zeit ∆t anströmen, gilt
F R ∼ ∆N mv
∆t
Nach Abschnitt C.2.c gilt ∆N = vnA . Hierin ist n die Anzahl der Teilchen pro Volumen. Die
∆t
Reibungskraft ist also proportional
F R ∼ Anmv 2
F R = c W A 1 ρv 2
2
Man schreibt
cW ist der Widerstandsbeiwert, der von der Form und der Oberflächenbeschaffenheit des Körpers abhängt, nm = ρ ist die Dichte der Flüssigkeit bzw. des Gases.
Bei kleineren Geschwindigkeiten stoßen die strömenden Teilchen nicht mehr frontal gegen
den Körper, sondern sie umströmen ihn auf einer glatten Bahn. Man spricht dann von laminarer Strömung. Die Reibung entsteht durch Impulsaustausch von Teilchen, die zwischen aneinander vorbeigleitenden Flüssigkeitsschichten ausgetauscht werden. Diese Reibung nennt man
innere Reibung von Flüssigkeiten. Sie wird durch den Koeffizienten der Viskosität η beschrieben. Nach Newton definiert man für eine ebene Strömung in Richtung x, deren Geschwindigdv
keit sich in einer Richtung y senkrecht zu den Flüssigkeitsschichten ändert: x ≠ 0
dy
FR = η
dv x
A
dy
Im Gegensatz zur Reibung zwischen festen Körpern ist die innere Reibung von der Fläche abhängig. Der Viskositätskoeffizient hat gemäß der obigen Definition die Dimension
62
[η] = Ns/m2. Strömungen werden genauer im Kapitel Hydrodynamik (Kapitel D.4.c) behandelt. Zur Berechnung einfacher Bewegungen unter dem Einfluß einer Reibungskraft benötigen
wir im folgenden nur die Reibung auf eine Kugel mit dem Radius R bei laminarer Strömung
(s. Abb. 50).
Abb. 50: Die Stromlinien bei laminarer Strömung um eine Kugel.
Hierfür gilt das Stokesche Gesetz
F R = 6πηRv
Bei laminarer Strömung ist die Reibungskraft also proportional zur Geschwindigkeit. Bei höheren Geschwindigkeiten ist sie, wie wir gesehen hatten, proportional zu v2. In der Nähe der
Schallgeschwindigkeit nimmt FR dramatisch zu. Insgesamt ergibt sich für FR/v2 in Abhängigkeit von v nebenstehender Verlauf (Abb. 51). Bei kleinen Geschwindigkeiten ist FR/v2 ~ 1/v
(FR ~ v), in einem weiten Bereich ist FR/v2 konstant (FR ~ v2).
Abb.51: Wie die Reibungskraft an einem Körper in einer
Strömung von der Geschwindigkeit der Strömung abhängt.
3. Beispiele für einfache Bewegungen
a) In zäher Flüssigkeit fallende Kugel
Abb. 52: Auf eine in einer zähen Flüssigkeit fallenden Kugel wirkt neben der Schwerkraft die Reibungskraft, eventuell noch die Auftriebskraft.
63
Die Bewegungsgleichung lautet
•
m v = FG − FR
FG ist die um den Auftrieb verringerte Gewichtskraft. Im folgenden wird angenommen, daß
der Auftrieb vernachlässigbar ist FG = mg. Für die Reibungskraft wird das Stokessche Gesetz
vorausgesetzt: FR = mαv, wobei α = 6πηR/m. Damit erhält man aus der Bewegungsgleichung
eine Differentialgleichung für v
•
v = g − αv
Man dividiert durch die rechte Seite und kann sofort integrieren.
dv
dt
dt
∫ g − αv = ∫ g − αv = t
dv
Das erste Gleichheitszeichen verwendet die Substitutionsregel ∫ F[z(x)]dx = ∫ F(z) dx dz
dz
Man substituiert g - αv = z. Mit dz = -αdv erhält man
1
−α
∫
dz = − 1 ln z − c = − 1 ln (g − αv) − c = t
z
α
α
Die Integrationskonstante c wird aus den Anfangsbedingungen bestimmt. Es soll gelten für
t = 0 v = 0. Dies in die Endformel eingesetzt ergibt
1 ln g
c = −α
Damit wird das Gesamtergebnis
1 ln (g − αv) + 1 ln g = t
−α
α
ln
g − αv
g = −αt
ln (g − αv) − ln g = −αt
64
Um das v(t) Gesetz zu erhalten, muß nach v aufgelöst werden. Zunächst wird nach dem Argument von ln: (1 - αv/g) über die Beziehung lnex = x aufgelöst
-
α
1 − g v = e −αt
Das v(t) Gesetz lautet damit
g
v = α (1 − e −αt ) =v 0 (1 − e −αt )
Für t >> 1/α wird v = v0. v0 ist die asymptotisch erreichte Grenzgeschwindigkeit.
g
gm
∼ R 2 da m = ρ 4π R 3
v0 = α =
6πηR
3
Abb. 53: Oben: die e - Funktion. Unten: die Entwicklung der
Geschwindigkeit des fallenden Tropfens.
Die Grenzgeschwindigkeit v0 ist nach einigen Zeiten t0 = 1/α erreicht, was u.U. eine sehr kurze Zeit sein kann. Man kann also so rechnen, als ob der Körper abgesehen von einer kurzen
Anfangsphase mit der Geschwindigkeit v0 fliegt. Daher fallen große Regentropfen schneller
als kleine. In Wolken sind die Wassertröpfchen extrem klein. Sie fallen daher so langsam, daß
sie praktisch schweben. In der anfänglichen Beschleunigungsphase entspricht das Verhalten
von v dem der Ladung Q beim Aufladen eines Kondensators. dv/dt nimmt laut Bewegungsgleichung mit steigendem v ab. Beim Kondensator nimmt dQ/dt durch das Gegenfeld ab.
b) Reibungsfreie Bewegung auf einer schiefen Ebene
Die antreibende Kraft in Bewegungsrichtung ist (s. Abb. 54) Ft = mg·sinα. Es ergibt sich also
eine konstant beschleunigte Bewegung mit der gegenüber dem freien Fall reduzierten
Beschleunigung
a = g·sinα
65
Abb. 54: Die schiefe Ebene eignet sich dazu, eine gleichförmig beschleunigte Bewegung zu untersuchen.
Um v(t) und s(t) zu finden geht man also wie bei der Behandlung der gleichförmig beschleunigten Bewegung in Kap. B.e vor.
c) Die Atwoodsche Fallmaschine
Abb. 55: Bei der Atwoodschen Fallmaschine ist die Trägheit
durch die Summe der Massen, die antreibende Kraft durch
die Differenz der Gewichte der Massen gegeben.
Betrachtet wird ein System aus zwei Massen, die an den beiden Seiten eines Fadens hängen,
der über eine Rolle geführt wird (Abb. 55). Auf die Massen wirkt neben der Schwerkraft die
Kraft, die von der jeweils anderen Masse über den Faden übertragen wird. Wenn man in solcher Situation unsicher ist, ob eine Kraft übertragen wird, schneide man den Faden in einem
Gedankenexperiment durch und prüfe, ob die Dynamik sich ändert. Die Kraft F, mit der der
Faden gespannt wird, wird zunächst als Unbekannte eingeführt. Es ergeben sich zwei Bewegungsgleichungen für die Massen m1 und m2, aus denen die unbekannte Kraft F eliminiert
werden kann.
••
m2g − F = m2 x
••
F − m1g = m1 x
Durch Addition beider Gleichungen erhält man
••
(m 2 − m 1 )g = (m 1 + m 2 ) x
••
x=
m2 − m1
g
m1 + m2
66
Bei dieser Betrachtung wurde die Trägheit der Rolle vernachlässigt. Man erhält also wieder
eine gleichförmig beschleunigte Bewegung. Die zu beschleunigende Masse ist hier m1 + m2,
die antreibende Kraft (m2 - m1)g. Die Fadenspannung ergibt sich aus einer der beiden Ausgangsgleichungen zu
F=
2m 1 m 2
g
m1 + m2
die Kraft, die die Aufhängung aufbringen muß ist 2F
d) Die Rakete
Abb. 56: Zur Ableitung der Raketengleichung. dm ist ein Massenelement des Treibstoffs. Alle Geschwindigkeiten werden in
Vorwärtsrichtung als positiv gerechnet.
Betrachtet wird eine Rakete im Weltraum in so großer Entfernung von den anderen Himmelskörpern, daß die Gravitationskräfte keine Rolle spielen. Im ruhenden Bezugssystem ist die Geschwindigkeit der Rakete v, die des Gases vgas, die Ausströmgeschwindigkeit des vom Antrieb
ausgestoßenen Gases von der Rakete aus betrachtet ve, wobei die positive Richtung für alle
Geschwindigkeiten in Bewegungsrichtung der Rakete zeigen soll. ve und vgas hängen über die
Raketengeschwindigkeit v voneinander ab. v + ve = vgas. Um auszurechnen, wie sich v in Abhängigkeit vom Massenausstoß entwickelt, wird der Impulssatz dp/dt = 0 für das gesamte System betrachtet. Wenn die Raketenmasse um |dm| abnimmt, nimmt die Masse des ausgestoßenen Gases um |dm| zu: dmRakete = - dmgas.
p(t + dt) = (m + dm)(v +dv) − dmv gas
Beim Grenzübergang verschwinden Terme zweiter Ordnung
p(t + dt) = mv +mdv + vdm − dmv gas
Da v + ve = vgas und damit vdm - vgasdm = -vedm, wird daraus
67
p(t + dt) = mv +mdv - v e dm
Die Impulsänderung dp = p(t + dt) - p(t) wird damit
dp = mdv - vedm
Diese soll verschwinden, da nur innere Kräfte wirken
mdv = vedm, d.h. dv = v e dm
m
Diese Gleichung läßt sich sofort integrieren: v = velnm + C
Die Integrationskonstante C wird durch die Anfangsbedingungen festgelegt: v = v0, wenn
m = m0. Eingesetzt ergibt dies: C = v0 - velnm0 und
v = velnm + v0 - ve lnm0
mit dem Ergebnis
m
v = v 0 − v e ln m0
Da m0 > m und nach Definition ve < 0, nimmt v zu. Bei chemischen Raketen kann die Ausströmgeschwindigkeit ve einen gewissen Wert nicht überschreiten. Außerdem hat m0/m einen
maximalen Wert, da man ein gewisses Strukturgewicht m0 braucht, um den Treibstoff m - m0
zu halten. Als Konsequenz kann die Rakete eine gewisse Endgeschwindigkeit nicht überschreiten. Als Ausweg bieten sich mehrstufige Raketen an und elektrische Antriebe, die sehr
viel höhere Ausstoßgeschwindigkeiten erlauben als chemische Antriebe, meisten allerdings
nur relativ kleine Massendurchflüsse.
e) Dynamik der Kreisbewegung
Für den allgemeinen Fall spaltet man die Bewegungsgleichung in einen tangentialen und einen
normalen Anteil auf (s. Abb. 58). Da p = p·et und et von der Zeit abhängt, gilt
F=
dp •
•
=p e t + p e t
dt
68
Abb. 57: Die Kreisbewegung wird in eine tangentiale und
eine normale Bewegung aufgespalten.
•
•
Hier sind F t =p e t die tangentiale Impulsänderung und F n = p e t . Nach dem bei der Kinematik der Kreisbewegung gesagtem (Kap. B.2.f) kann man hierfür schreiben
F n = mRω 2 e n
•
Bei einer gleichförmigen Kreisbewegung ist p = 0 . Der Körper erfährt nur eine Beschleunigung mRω2 senkrecht zur Bahn. Diese muß durch eine Kraft, die senkrecht zur Bahn steht und
konstanten Betrag besitzt, erzeugt werden. Umgekehrt kann man sagen, daß ein Körper, der
nur eine konstante Beschleunigung senkrecht zu v erfährt, eine Kreisbewegung ausführt.
f) Geladenes Teilchen im Magnetfeld
Abb. 58: Die Lorentzkraft steht immer senkrecht auf der
Geschwindigkeit. Daher ergibt sich eine Kreisbewegung.
Die Kraft auf ein geladenes Teilchen der Ladung e0 im Magnetfeld ist
F = e0v × B
Nach Definition des Vektorproduktes (s. Abb. 58) steht F immer senkrecht zu v. Damit steht
auch a senkrecht zu v. Die Teilchen vollführen also eine Kreisbahn. (Wenn v eine Komponente in B - Richtung hat, laufen sie auf einer Spirale). Die Zentripetalkraft ist die Lorentzkraft.
mrω 2 = e 0 vB
Mit v = ωr erhält man
mrω 2 = e 0 ωrB. Hieraus ergibt sich die Kreisfrequenz des Um-
laufes, die Gyrations- oder Zyklotronfrequenz ωc und der Radius der Kreisbahn, der sogenannten Gyrationsradius.
e0B
ωc = m
v = vm
rc = ω
e0B
69
Abb. 59: Prinzipieller Aufbau eines Zyklotrons
Im Zyklotron (Abb. 59) werden Teilchen beschleunigt, indem sie durch ein Magnetfeld nahezu auf Kreisbahnen gehalten werden und dadurch wiederholt in einem elektrischen Feld zwischen den D förmigen Elektroden eine Beschleunigung in Bahnrichtung erhalten. Der Radius
der Bahn nimmt mit zunehmender Geschwindigkeit zu, die Frequenz bleibt, solange klassisch
gerechnet werden kann, konstant. Eine andere Anwendung der Gyrationsbewegung ist der
Einschluß von geladenen Teilchen in heißen Gasen senkrecht zum Magnetfeld.
g) Kurvenneigung
Abb. 60: Die Fahrbahn muß in der Kurve geneigt sein, um
eine radiale Kraftkomponente der Schwerkraft zu erhalten,
die die Kreisbewegung ermöglicht.
Die optimale Neigung der Fahrbahn liegt dann vor, wenn der Motorradfahrer bei Kurvenfahrt
senkrecht zur Straßendecke steht (s. Abb. 60). Die Schwerkraft hat zwei Aufgaben: Aufbringen der Auflagekraft FN und der Zentripetalkraft Fp. Wir zerlegen daher die Schwerkraft in eine horizontale Komponente und eine, die senkrecht auf der Fahrbahn steht. Dann ist der Winkel α in dem Kräfteparallelogram in Abb. 60 gerade der Neigungswinkel der Bahn. Aus dem
Kräfteparallelogramm ermittelt man
tan α =
F p mRω 2 v 2
= mg =
FG
Rg
h) Das Geoid
Abb. 61: Die Oberfläche stellt sich so ein, daß sie senkrecht auf
der Komponente steht, die übrig bleibt, wenn man die Zentripetalkraft die die Kreisbewegung besorgt, abzieht. Anschaulicher ist
die Erklärung über Scheinkräfte (s. Abb. 106).
70
Ein frei bewegliches Massenelement an der Oberfläche der Erde bewegt sich auf der Oberfläche solange, bis es keine parallel zur Oberfläche wirkende Kraft mehr spürt. Die Schwerkraft
FG, die zum Erdmittelpunkt gerichtet ist, muß die Normalkraft FN und die für die Kreisbewegung erforderliche Zentripetalkraft Fp aufbringen. Die entsprechende Kraftzerlegung wird in
Abb. 62 gezeigt. Man erkennt, daß die Erdoberfläche, die sich ja senkrecht zu FN einstellen
muß, gegen der Kugeloberfläche geneigt ist. Die radiale Richtung, die auf den Erdmittelpunkt
zeigt, ist verschieden von der vertikalen Richtung, die ein Lot anzeigt.
4. Drehimpuls und Drehmoment
Während die Grundgesetze der Dynamik wie die meisten Grundgesetze der Physik leicht hinzuschreiben sind, ist ihre Anwendung im allgemeinen außerordentlich mühselig. In der Regel
muß man daher fast immer drastische Vereinfachungen vornehmen. Selbst dann wären viele
Probleme nicht zu bewältigen, wenn man nicht auf einige nützliche Hilfsbegriffe wie Impuls,
Drehimpuls, Energie zurückgreifen könnte. Um diese Hilfsbegriffe geht es in den folgenden
Abschnitten.
Drehimpuls und Drehmoment sind Größen, die besonders für die Beschreibung von Drehbewegungen geeignet sind. Sie sind aber für eine beliebige Bewegung eines Massenpunktes definiert. Drehmoment und Drehimpuls erfordern einen Bezugspunkt. Bei einer Drehung um eine Achse wählt man häufig als Bezugspunkt einen Punkt auf dieser Drehachse. Bei einer
Bahnbewegung etwa der Planeten ist das Kraftzentrum ein geeigneter Punkt. Man kann aber
auch jeden beliebigen anderen Punkt wählen.
a) Der Drehimpuls
Man definiert den Drehimpuls eines Massenpunktes bezüglich eines Bezugspunktes als
(2)
L=r×p
Abb. 62: Zur Definition des Drehimpulses
Dies ist gleichbedeutend mit L = mr × v . r ist dabei der Vektor, der vom Bezugspunkt zum
Massenpunkt zeigt. Da bei einer ebenen Bewegung, wenn r in der Bahnebene liegt, der
71
Vektor ω senkrecht zu r und v steht, steht in dieser Geometrie L parallel zu ω, und man kann
schreiben
L = mr2ω
Wenn r nicht in der Bahnebene liegt, hat L nicht die gleiche Richtung wie ω. Die Richtung
von L ändert sich während der Bewegung. Zerlegt man v in einen radialen und einen azimutalen Anteil (s. Abb.63)
Abb. 63: Zerlegung der Geschwindigkeit in Radial - und Azimutalanteil.
v = vθ +vr
erhält man, da r × v r = 0
L = mr × (v θ + v r ) = mr × v θ + mr × v r = mr × v θ
Für den Drehimpuls ist also nur die zu r senkrechte Geschwindigkeitskomponente maßgeblich. Für eine ebene Bewegung, bei der r in der Ebene der Bewegung liegt, gilt
•
•
v θ = rω, ω =θ und damit L = mr 2 θ = mrv θ
b) Das Drehmoment
Durch Ableitung des Drehimpulses nach der Zeit erhält man
dL = dr × p + r × dp
dt
dt dt
Da dr = v und p = mv, verschwindet der erste Term auf der rechten Seite. Da außerdem
dt
dp
= F , erhält man
dt
dL = r × F
dt
72
Abb. 64: Zur Definition des Drehmomentes. Die radiale Komponente von F liefert keinen Beitrag.
Es ist daher sinnvoll, die rechte Seite als eine neue Größe zu definieren. Man nennt sie das
Drehmoment.
(3)
M= r×F
Man erhält dann für die Änderung des Drehimpulses eine Gleichung, die völlig analog zum
Aktionsgesetz ist. Man muß nur die Kraft durch das Drehmoment und den Impuls durch den
Drehimpuls ersetzen.
(4)
M = dL
dt
Das Drehmoment übernimmt also bei Drehbewegungen die Rolle der Kraft in Translationen,
der Drehimpuls die Rolle des Impulses. Mit der gleichen Argumentation wie oben beim Drehimpuls findet man, daß zum Drehmoment nur die Kraftkomponente beiträgt, die senkrecht auf
r steht. Bei der Beschreibung von Drehbewegungen ist es häufig zweckmäßig, Polarkoordina•
•
ten einzuführen. Statt s nimmt man den Drehwinkel θ, statt v = s nimmt man ω = θ . Der
Vergleich von p = mv und L = mr2ω zeigt, daß man statt der Masse bei Drehbewegungen
zweckmäßigerweise das Trägheitsmoment J = mr2 verwendet. Man definiert daher das Trägheitsmoment eines Massenpunktes auf einer Kreisbahn mit Radius R:
(5)
J = mR 2
c) Der Flächensatz
Abb. 65: Beim Flächensatz geht es um die Fläche, die der
Fahrstrahl r überstreicht.
73
Wenn kein äußeres Drehmoment wirkt (M = 0), d.h. wenn F = 0, oder wenn F parallel zu r
steht, d.h. eine Zentralkraft wirkt, wird nach Gleichung (4) dL = 0 und L bleibt konstant. Dardt
aus folgt zunächst, daß die Bewegung eben ist. Außerdem ist L = mrv konstant, d.h. je größer
r, z.B. der Abstand zum Kraftzentrum ist, desto kleiner wird die Geschwindigkeit. Nach Kepler drückt man diese Tatsache mit dem Flächensatz aus. Die bei dem Fortschreiten um einen
Winkel dθ vom Fahrstrahl, d. h. dem Strahl, der vom Kraftzentrum zum umlaufenden Körper
zeigt, überstrichene Fläche ist nach Abb. 65
dA = 1 r ⋅ rdθ
2
Die Gesamtfläche bei Fortschreiten um einen endlichen Winkel ist dann
θ2
Σ 12 r 2 ∆θ = 12 ∫ θ
∆θ→0
A = lim
r 2 dθ
1
Damit wird die Geschwindigkeit, mit der die überstrichene Fläche sich ändert
dA = dA dθ = 1 r 2 dθ
dt dθ dt 2 dt
Dieser Ausdruck ist konstant, da nach dem Drehimpulssatz beim Fehlen äußerer Drehmomente L = mr2dθ/dt konstant ist. Der Drehimpulssatz und der Flächensatz beschreiben also den
gleichen Sachverhalt. Für die Planetenbewegung besagt der Drehimpulssatz, daß der Fahrstrahl von der Sonne zu einem Planeten in gleichen Zeiten gleiche Flächen überstreicht.
Man beachte, daß der Drehimpuls eines Körpers auf einer Bahn auch dann noch konstant bleiben kann, wenn äußere Kräfte auf den Körper wirken, nämlich, wenn diese Zentralkräfte sind.
Man beachte außerdem, daß auch ein gleichförmig geradlinig bewegter Körper einen Drehimpuls bezüglich eines Punktes, der nicht auf seiner Bahn liegt, hat. Für eine geradlinige Bewegung ist L = mrv sinα = m·d·v = const. (s. Abb.66).
Abb. 66: Auch eine geradlinige Bewegung hat einen
Drehimpuls
74
5. Arbeit, Leistung, Energie
a) Grundbegriffe
Der Begriff Arbeit leitet sich aus den schon in der Antike bekannten Tatsachen her, daß man
mit einfachen Maschinen wie Hebelarmen oder Flaschenzügen zwar die Kraft, die notwendig
ist, ein Gewicht zu heben, verkleinern kann, dafür aber eine entsprechend größere Strecke zurücklegen muß. D.h. F·s bleibt gleich. Man sagt daher, wenn ein Körper durch eine Kraft verschoben oder verformt wird, leistet die Kraft eine Arbeit. Bei konstanter Kraft ist die Arbeit
W = Fs·s, wobei Fs die Komponente der Kraft in Richtung der Verschiebung ist. Bei unterschiedlicher Richtung von F und s kann man die Kraftkomponente von F in Richtung s durch
F und den Winkel ausdrücken: W = F·s·cos α.
Abb. 67: Nur die Kraftkomponente in Richtung der
Verschiebung leistet Arbeit.
Für eine veränderliche Kraft gilt für genügend kleine Wegstrecken ∆s
∆W = F(s) · ∆s
Daher ist die allgemeine Definition der Arbeit
s2
W = ∫ F • ds
(6)
s1
Die Dimension der Arbeit ist [W] = Nm = kgm2/s2 =J(Joule).
Die Leistung ist ein Maß dafür, wieviel Arbeit pro Zeiteinheit verrichtet wird
P = dW
dt
Die Dimension der Leistung ergibt sich aus der Definition [P]=Nm/s = Joule/s = W (Watt).
75
Energie ist die Fähigkeit, Arbeit zu leisten. Sie hat also die gleiche Dimension wie Arbeit.
Wirkungsgrad η ist das Verhältnis von Nutzarbeit zu aufgewendeter Arbeit, ist also eine dimensionslose Konstante, im allgemeinen kleiner als eins.
b) Berechnung des Integrals ∫ F • ds
∫ F • ds ist eine neue Form eines Integrals. Bisher war ds ein Skalar. Es gibt verschiedene
Möglichkeiten, aus dem Skalarprodukt Integrale der üblichen skalaren Schreibweise zu erhalten, indem man formal die verschiedenen Schreibweisen des Skalarproduktes anwendet.
F • ds = F x dx + F y dy + F z dz
∫ F • ds = ∫ F x dx + ∫ F y dy + ∫ F z dz
Man erhält die Summe von drei Integralen über die verschiedenen Koordinaten. Oder
F • ds = (F cos α)ds
Hier muß man sich Gedanken machen, wie sich in dem konkreten Beispiel α entlang des Weges ändert. Ist diese Funktion bekannt, liegt wieder ein normales Integral vor. Besonders einfach wird die Berechnung in diesem Fall, wenn α konstant oder wenigstens stückweise konstant ist. Wenn Fs (s) = Fs(s)cosα(s) bekannt ist, erhält man
s2
W = ∫ F s (s)ds
s
mit der Umkehrung
F s (s) =
dW(s)
ds
Wenn die Bahnkurve in Parameterdarstellung bekannt ist, r = r(t), transformiert man im Integral die Variablen x,y,z auf t:
r2
t2
W = ∫ F(r) • dr = ∫ F[r(t)] • dr = ∫  F(t) • dr  dt
r1
t1
dt
76
Die Arbeit hat ein Vorzeichen. Wenn man als Kraft die äußere Kraft wählt, die auf das System
wirkt, heißt positive Arbeit, daß an dem System Arbeit geleistet wird. Die Energie des Systems erhöht sich. Negative Arbeit ist vom System geleistete Arbeit. Nach dem Reaktionsprinzip existiert zu jeder Kraft eine gleich große Gegenkraft. Wenn man diese Gegenkraft, die
vom System auf die Umgebung wirkt, zur Berechnung der Arbeit verwendet, ist positive Arbeit die, die das System leistet.
Man sagt, ∫ F(r) • dr ist ein Kurvenintegral entlang der Kurve C.
C
Beispiel:
i. Welche Arbeit benötigt man zum Ausziehen einer Feder um die Strecke h?
Kraftgesetz: F = Dx
h
h
W = ∫ Dxdx =  1 Dx 2  = 1 Dh 2
0
2
0 2
ii. Arbeit der Zentripetalkraft bei gleichförmiger Kreisbewegung
Parameterdarstellung der Bahn (s. Abb. 68):
x = Rcos ωt
y = Rsin ωt
dx = -Rωsin ωt
dy = Rωcos ωt
Fx = -(mv2/R)cosωt
Fy = -(mv2/R)sinωt
W = ∫ F x dx + ∫ F y dy = mv 2 ω  ∫ sin ωt cos ωtdt − ∫ cos ωt sin ωtdt  =
Abb. 68: Welche Arbeit leistet die Zentripetalkraft?
77
Dieses Ergebnis ergibt sich auch sofort aus der Bedingung, daß die Zentripetalkraft senkrecht
auf der Bewegungsrichtung des Körpers steht.
c) Die potentielle Energie
α) Was ist potentielle Energie
Bei manchen Kraftfeldern F(r) wie dem Gravitationsfeld ist die Arbeit, die man benötigt, um
einen Körper von einem Anfangspunkt zu einem Endpunkt zu bewegen, unabhängig von der
Form des dazwischen liegenden Weges. Diese Kraftfelder heißen konservativ. Als Beispiel
wird im folgenden gezeigt, daß das Gravitationsfeld in der Nähe der Erdoberfläche, d.h. bei
F = const konservativ ist. Dazu betrachten wir einen Körper, der in diesem Feld auf einer
schiefen Ebene von A nach B bewegt wird (Abb. 69).
Abb. 69: Die Arbeit beim Heben einer Masse m auf der
schiefen Ebene.
Dabei leistet das Gravitationsfeld die Arbeit
W = Fts = mgs sin α = mgH
Die Arbeit ist die gleiche, wie wenn der Körper senkrecht die Strecke H fallen würde. Daher
ist sie auch auf einer aus schiefen Ebenen mit unterschiedlicher Neigung zusammengesetzten
Bahn wie in Abb. 70 und folglich für eine Bahn beliebiger Form mgH.
B
B
A
∫ A F • ds =∫ A F • ds = −∫ B F • ds
C
C
(7)
C
Abb. 70: Die Arbeit ist nur von H, nicht von der Neigung der
Ebene abhängig. daher ergibt sie sich auch bei zusammengesetzten Ebenen aus der Gesamthöhe.
Im Integral ganz rechts durchläuft man die Bahn C2 von B nach A. Gleichung (7) besagt, daß
die bei der Bewegung des Körpers von A nach B hinengesteckte Energie vollständig
78
Abb. 71: Die Arbeit entlang eines geschlossenen Weges
zurückgewonnen werden kann, wenn der Körper zum Anfangspunkt zurückkehrt. Dabei kann
die Form des Rückweges sich von der des Hinweges unterscheiden. Gleichung (7) kann auch
geschrieben werden
B
A
∫ A F • ds +∫ B F • ds
C
=0
C
In einem konstanten Kraftfeld ist die Arbeit entlang eines geschlossenen Weges unabhängig
von der Form des Weges 0
∫ F • ds
=0
Der Kreis am Integralzeichen zeigt bei einem Linienintegral an, daß über einen geschlossenen
Weg integriert werden muß. Das Integral besagt anschaulich, daß man bei einer Radtour in
bergigem Gelände, die zum Ausgangspunkt zurückführt, genau so viel Energie in den Gefällestrecken gewinnt, wie man auf den Steigungen hineingesteckt hat, unabhhängig davon, wie
Strecken mit Steigung und Gefälle auf der gesamten Tour angeordnet sind. Reibungseffekte
müssen allerdings vernachlässigbar sein.
Die obige Überlegung kann man sofort auf ein Zentralfeld, in dem die Kraft nur vom Abstand
zum Zentrum abhängt, erweitern. An jedem Ort kann die Kraft F und das Wegelement ∆s in
eine radiale und eine azimuthale Komponente zerlegt werden.
F = F θ + Fr
Damit wird die Arbeit entlang ∆s
∆W = F·∆s = Fθ ∆sθ + Fr ∆r
79
Da Fθ = 0 - Dies gilt für alle Zentralfelder- ist ∆W = Fr∆r, und
rB
W = ∫ F r dr
rA
Die Arbeit längs des krummlinigen Weges von A nach B ist die gleiche wie wenn der Körper
vom Anfangs- zum Endradius bewegt wird und und deshalb unabhängig von der Form des
Weges.
Konservativ sind alle Zentralfelder, ebenso elastische Kräfte. Nichtkonservativ sind Reibungskräfte. Bei konservativen Kräften kann man die Arbeit, die angewandt werden muß, um einen
Körper von einem festen Anfangspunkt zu einem beliebigen anderen Punkt im Raum zu bringen als Feldgröße definieren. Da diese Arbeit bei festem Anfangs - und Endpunkt unabhängig
vom Weg ist, kann man jedem Punkt im Raum einen bestimmten Arbeitswert zuordnen. Diesen nennt man potentielle Energie. Merke:
Eine potentielle Energie kann nur bei konservativen Kräften sinnvoll definiert werden
Die Potentielle Energie ist bezüglich eines beliebigen Anfangspunktes definiert.
Den Anfangspunkt muß man am Anfang einer Betrachtung festlegen.
β) Äquipotentialflächen
Abb. 72: Das Gravitationsfeld einer Kugel besteht aus radial gerichteten Kräften und kugelförmigen konzentrischen
Äquipotentialflächen.
Bewegt man sich in einem Kraftfeld senkrecht zur örtlichen Kraftrichtung, so wird keine Arbeit geleistet. Alle Punkte, die durch eine solche Bewegung erreichbar sind, haben gleiche potentielle Energie. Sie liegen auf einer Fläche. Man nennt diese Flächen daher Äquipotentialflächen. Bei kugelsymmetrischen Massen sind es konzentrische Kugelflächen, in homogenen
Kraftfeldern (F = const.) sind es parallele Ebenen.
Zur Definition der potentiellen Energie benutzt man daher statt eines Anfangspunktes eine
Anfangs Äquipotentialfläche, der man willkürlich das Potential 0 erteilt. Die Willkür stört in
der Anwendung nicht, da man sich nur für Differenzen der potentiellen Energie interessiert.
Bei ebenen Problemen nimmt man häufig die Fläche mit der niedrigst vorkommenden
80
potentiellen Energie, z.B. den Laborfußboden. Bei kugelsymmetrischen Anordnungen bevorzugt man eine Fläche im Unendlichen.
γ) Das Vorzeichen
Man definiert die potentielle Energie des Kraftfeldes F(r) über
r
W pot (r) = −∫ F(r) • dr
(8)
r0
r0 ist ein Punkt auf dem Anfangsniveau. Durch das Minuszeichen erreicht man, daß Wpot posi-
tiv wird, wenn man Arbeit in das System hineinsteckt, d.h. wenn ∫ F ext • dr > 0, aber zur Berechnung der potentiellen Energie nicht die äußere Kraft Fext sondern die Kraft des Feldes
F = -Fext verwendet wird.
Abb. 73: In der Definition des Potentials steht die innere
Kraft des Systems. Diese ist z.B. beim Erdfeld nach unten
gerichtet.
Bewegt sich z.B. ein Körper im Erdfeld etwa auf grund seiner anfänglichen kinetischen Energie nach oben, so ist er nur der Anziehungskraft ausgesetzt, und diese ist entgegen seiner Bewegungsrichtung ausgerichtet (Abb. 73).
FG = -mg
h
W pot = −∫ (−mg)dx = mgh
Die potentielle Energie nimmt also zu, wie wir erwarten, wenn ein Körper angehoben wird.
δ) Arbeit im Potentialfeld
Der Potentialbegriff erlaubt es, Arbeit, die an einem Körper bei der Bewegung im Potentialfeld geleistet wurde, durch Differenzen der potentiellen Energie auszudrücken. Die Arbeit, die
die innere Kraft bei einer Bewegung von A nach B leistet, ist
B
r0
B
A
B
A
A
r0
r0
r0
W AB = ∫ F • dr = ∫ F • dr + ∫ F • dr = −∫ F • dr + ∫ F • dr
81
W AB = W pot (A) − W pot (B)
(9)
Beispiel: Die potentielle Energie des Gravitationsfeldes einer Punktmasse M
Die Kraft auf eine Probemasse m im Abstand r ist gegeben durch
r
F = −γ Mm
2 r
Damit wird die potentielle Energie
W pot = −∫
r
r0
r
r 1
−γmM
 1  = −γmM  1 − 1 
=
γmM
=
−γMm
dr
dr
∫ r0 r 2
 r r0 
 r 0  r0
r2
Das Anfangsniveau setzt man so, daß der zweite Term in der eckigen Klammer verschwindet
r0 = ∞
Die potentielle Energie ist also
W pot = −γMm 1r
Abb. 74: Das Gravitationspotential einer Punktmasse oder
einer Kugel.
ε) Das Potential
Um eine Größe unabhängig von der Probemasse m zu erhalten, definiert man ähnlich wie bei
der Feldsstärke G =F/m das Potential
W pot
V= m
Damit wird das Potential eines Massenpunktes (oder einer Kugel) der Masse M
82
γM
V=− r
η) Potentialkurven
Abb. 75: Potentialkurven erlauben eine anschauliche Vorstellung von den möglichen Bewegungsvorgängen.
Bewegt sich ein Körper reibungsfrei im Gravitationsfeld der Erde in der Nähe der Erdoberfläche (bei F = const) auf einem Höhenprofil h(x), so hat er die potentielle Energie mgh(x) und
das Potential gh(x). Dieses bestimmt die Kraft und damit die Bewegung. Die tangentielle
Komponente der Schwerkraft ist Ft = mg sinα. Für α << 1 gilt sin α ~ tanα ~ α und damit
F t ≈ mgα ≈ mg
dh(x)
dx
(α ≈ tan α =
dh(x)
)
dx
Andererseits bewegt sich ein Körper in einem vorgegebenen Feld mit der potentiellen Energie
W(x) unter der Kraft
Fx =
dW(x)
dx
Wenn man mgh(x) mit W(x) und Ft mit Fx identifiziert - was bei kleinen Winkeln nicht all zu
kühn ist - erkennt man, daß beide Bewegungen gleich sind. Wir können uns also die Bewegung eines beliebigen Körpers im Potential V(x) durch die Bewegung einer Kugel im Höhenprofil h(x) ~ V(x) veranschaulichen. Da uns von unserer Erfahrung Bewegungen im Potentialgebirge an der Erdoberfläche vertraut sind, gibt uns dies die Möglichkeit intuitiv Bewegungsabläufe voraus zu sagen und damit Lösungsansätze für die Differentialgleichungen, zu denen
theoretische Betrachtungen führen, anzugeben. Dieses Verfahren läßt sich auch auf zweidimensionale Potentialverteilungen V(x,y) erweitern. Man betrachtet dann die Bewegung einer
Kugel im Gebirge h(x,y), das sich über der xy - Ebene erhebt.
Beispiele:
83
i. Molekül mit Ionenbindung
Abb. 76: Typisches Potential für die Bindung in einem Molekül. r ist der Abstand der Atome.
Für Ionenbindung kann die Bewegung eines Atoms im Feld des anderen oft durch ein Lennard
- Jones Potential angenähert werden.
6
r
r
W pot = −2  r0  +  r0 
12
Der Verlauf ist in Abb. 76 dargestellt. Der Gleichgewichtsabstand ergibt sich aus
−12
r 60
7
+ 12
r 12
0
13
dW pot
= 0.
dr
= 0 , mit der Lösung r = r0. Für r < r0 hat man eine abstoßende Kraft, für r > r0
eine anziehende. Die Energie W0 ist erforderlich, um den Abstand der Atome von r0 auf unendlich zu vergrößern. Dies entspricht der Dissoziation der Moleküls. W0 ist die
Dissoziationsarbeit.
ii. Die Wasserstoffusion
Abb.77: Außerhalb von r0 herrscht das Coulombpotential, innerhalb die Kernkräfte.
Bei der Verschmelzung zweier Deuteronen, d.h. zweier Kerne, die aus einem Proton und einem Neutron bestehen, zu Helium wird Energie frei. Bei großen Abständen gilt das
Coulombpotential
V pot =
1 e0
4πε 0 r
84
Etwa im Abstand des Deuteronendurchmessers r0 = 10-15 m beginnen die anziehenden Kräfte
der starken Wechselwirkung. Das Potential hat qualitativ den Verlauf von Abb. 77. Die zu
überwindende Potentialbarriere hat die Höhe
2
1, 6 2 (19 −19 )
e0
1
9
= 9 ⋅ 19
eV 0 =
Joule ≈ 2, 7 ⋅ 10 −13 Joule
4πε 0 r 0
10 −15
Dies entspricht nach der Definition E kin = 3 kT einer Temperatur
2
T=
2, 7 ⋅ 10 −13
E kin
=
= 10 10 K
−23
1, 5k 1, 5 ⋅ 1, 4 ⋅ 10
Quantenmechanisch gibt es eine gewisse Wahrscheinlichkeit, daß Teilchen mit kleinerer Energie den Potentialwall überwinden.
d) Die kinetische Energie
Abb. 78: Am Ende des Falls kann der Körper noch Arbeit
leisten. Er besitzt also Energie.
Um festzustellen, ob irgendein System einen Energieinhalt hat, kann man untersuchen, ob es
möglich ist, mit diesem System eine Spiralfeder zusammen zu drücken oder ein Gewicht zu
heben. Eine Masse mit der Geschwindigkeit v hat die Fähigkeit, eine Feder zusammenzudrükken. Also besitzt sie aufgrund ihrer Bewegung eine Energie. Wir nennen diese Energie kinetische Energie. Die kinetische Energie bestimmt man über die Arbeit, die bei der Beschleunigung von v0 auf v aufgewandt wurde.
Behauptung: diese ist bis auf eine Konstante W = 1 mv 2
2
Beweis:
Wir beweisen, daß d W(s) = F s (s) , wobei wir für W = 1/2 mv2 setzen und Fs die Kraft ist, die
ds
die Beschleunigung erzeugt hat.
d  1 mv 2  = mv dv = mv dv dt = m dv = F
s

ds  2
ds
dt ds
dt
85
Dies gilt für einen beliebigen Weg, entlang dem sich der Körper in einem beliebigen Kraftfeld
bewegt hat. Durch Integration erhält man
∫ F s ds = 2 mv 2 + C
1
Die Integrationskonstante C ergibt sich durch die Anfangsbedingungen: bei s = 0 sei v = v0.
Also
C = -(1/2)mv02
Die aufgewendete Arbeit findet sich vollständig in der Zunahme von (1/2)mv2 wieder.
∫ F s ds = 2 mv 2 − 2 mv 0
1
1
2
(10)
Am konkreten Beispiel der schiefen Ebene läßt sich verfolgen, wie man zu der Form
Ekin = (1/2)mv2 kommt. Wir stellen uns dazu vor, der Begriff der kinetischen Energie (und damit der Energiesatz) seien noch nicht bekannt. Um die Endgeschwindigkeit auf der schiefen
Ebene auszurechnen, stellen wir die Bewegungsgleichung auf und drücken die Endgeschwindigkeit durch H aus. Die Bahnbeschleunigung auf der schiefen Ebene ist (s. Abb. 54)
a = g sinα
Durch zweimalige Integration erhält man
v = gt sin α + v
s = (1/2)gt2sinα + v0t
Durch Elimination von t erhält man mit t =
s=
g(v-v 0 ) 2 g sin α
2g sin α
2
2
+v 0
v - v0
g sin α
(v-v 0 )
g sin α
gs sin α = gH = 1  (v-v 0 ) 2 + 2v 0 (v-v 0 ) =
2
1  v 2 − 2vv + v 2 + 2vv − 2v 2 
0
0
0
0
2
86
gH = 1 v 2 − 1 v 20
2
2
Die Endgeschwindigkeit ist nur von der durchlaufenen Höhe und der Anfangsgeschwindigkeit
abhängig, nicht von α, daher auch nicht von der Bahnform abhängig. Multipliziert man mit m,
erhält man den Energiesatz für dieses Problem
mgH + 1 mv 20 = 1 mv 2
2
2
e) Der Energiesatz der Mechanik
Aus den Gleichungen (9) und (10) ergibt sich sofort der Energiesatz für die Bewegung eines
Körpers unter dem Einfluß einer konservativen Kraft.
W kin (A) + W pot (A) = W kin (B) + W pot (B)
(11)
Die Summe aus kinetischer und potentieller Energie eines Körpers bleibt konstant, solange
nur konservative Kräfte auf ihn wirken. Beim Auftreffen eines Körpers auf einer Unterlage
nach dem freien Fall wird zumindest ein Teil der kinetischen Energie in Energie der chaotischen Bewegung der Atome umgewandelt. Diese heißt Wärme. Wenn Wärme eine Rolle
spielt, gilt der Energiesatz in der obigen Form nicht. Dies ist der Grund, warum sich der Energiesatz erst verhältnismäßig spät durchgesetzt hat. Im allgemeinen Fall muß man neben der kinetischen und der potentiellen Energie andere Energieformen mit berücksichtigen.
Die Grundkräfte zwischen Teilchen sind im allgemeinen konservativ, d.h. man kann für sie eine potentielle Energie definieren. Nur bei der magnetischen Kraft liegen die Verhältnisse
komplizierter. Bei der Bewegung eines ausgedehnten Körpers bewegt sich jedes der Teilchen,
aus denen der Körper besteht, in einem Potentialfeld. Wenn keine Energie in kinetische oder
potentielle Energie der ungeordneten Bewegung ("innere Energie") überführt wird, gilt der
Energiesatz in der einfachen Form der Gleichung (11) für das gesamte System. Daher ist die
Arbeit, die man bei einem Hebel oder Flaschenzug an einer Seite hineinsteckt, die gleiche, wie
die an der anderen Seite geleistete.
f) Verschiedene Energieformen
Die meisten Energieformen, mit denen man es im täglichen Leben zu tun hat, kann man auf
die potentielle Energie einer der Grundkräfte und die kinetische Energie zurückführen.
87
Chemische Energie ist die elektrostatische Energie der Moleküle, Kernenergie beruht im wesentlichen auf der potentiellen Energie der starken Wechselwirkung. Bei der Kernenergie wird
eine Eigenart der Energie wichtig, die für alle Energien gilt, aber klassisch im allgemeinen
keine Rolle spielt: Erhöht man die Energie in einem System, so erhöht sich laut Relativitätstheorie die Masse nach der Einsteinschen Formel
W = mc02 .
Darin ist c0 = 3·108 m/s die Lichtgeschwindigkeit. Im täglichen Leben ist die Massenerhöhung
wegen des Faktors c2 im allgemeinen verschwindend klein. Für Kernbausteine ist die Massenänderung durch Veränderung der Anregungsenergie ein entscheidender Faktor.
Wärmeenergie hat mit der Energie der ungeordneten Bewegung der Teilchen zu tun. Die genaue Begriffsbildung ist verwickelt und wird im Teil Wärme dieses Kurses erörtert. Einfach
definiert sind die Begriffe innere Energie und Temperatur. Die innere Energie U ist die Summe von mittlerer kinetischer und potentieller Energie der ungeordneten Bewegung aller Teilchen eines Körpers. Die Temperatur ist proportional zur mittleren kinetischen Energie der
Translation der ungeordneten Bewegung pro Teilchen. Man definiert für N Teilchen
1 mv 2 = 1
N
2
i=N
Σ= 12 m i v 2i = 32 kT
Hierin sind k = 1,38·10-23 J/K die Boltzmann Konstante und T die absolute Temperatur in Kelvin, wobei die Umrechnung in die Celsiusskala durch eine lineare Abhängigkeit mit
273K = 0C und 373K = 100C gegeben ist.
g) Anwendungen des Energiesatzes
α) Der Looping
Abb. 79: Ein Körper wird bei A losgelassen und rutscht reibungsfrei herunter. Fällt er bei B herunter?
88
Ein Fahrzeug werde im Punkt A losgelassen, um reibungsfrei eine schleifenförmige Bahn zu
durchfahren (s. Abb. 79). Bei welcher Höhe h muß es starten, um bei B nicht herunter zu
fallen?
Der Grenzfall liegt vor, wenn bei B die Schwerkraft gerade gleich der Zentripetalkraft ist.
(Dann ist die Auflagekraft gerade Null).
2
mg = m v
R
→
v 2 = Rg
Nach dem Energiesatz
Wpot(A) + Wkin(A) = Wpot(B) + Wkin(B)
gilt für v0 = 0 Wpot(A) = mgH, Wkin(A) = 0, Wpot(B) = 0, Wkin(B) = (1/2)mv2
gH + 0 = 0 + 1 mv 2
2
mit v2 = Rg und H = h - 2R wird daraus
g(h − 2R) = 1 Rg
2
→
h = 5R
2
β) Der harmonische Oszillator
Eine Masse m hänge an einer elastischen Feder. Für die Kraft, die die Feder auf die Masse
ausübt, wenn sie um die Strecke x aus der Gleichgewichtslage ausgelenkt wird, gilt F = -Dx.
Daher lautet das Aktionsgesetz
••
m x = −Dx
Für die Bewegung erhält man eine Differentialgleichung
••
x= − D
mx
89
Wer die Theorie der Differentialgleichungen kennt, hat vermutlich keine Schwierigkeit mit
der Lösung. Man macht eine sinusförmige Bewegung als Lösungsansatz Wir finden einen
solchen Lösungsansatz über das Potential und die Analogie mit der Bewegung einer Kugel in
dem entsprechenden Gebirge.
Die potentielle Energie ist
W pot = −∫ Fdx = 1 Dx 2
2
Das Potential hat also einen parabelförmigen Verlauf. Eine Kugel in einem derartigen Gebirge
würde eine Schwingung vollführen. Wir machen also den Ansatz
x = sinωt
und setzen dies in die Differentialgleichung ein, wobei
•
x = x 0 ω cos ωt
••
x = −x 0 ω 2 sin ωt
Es ergibt sich
−x 0 ω 2 sin ωt = − D
m x 0 sin ω
Der Ansatz löst also die Differentialgleichung, wenn ω2 = D/m. Der Körper schwingt sinusförmig (harmonisch) mit der Kreisfrequenz
ω=
D
m
Die Schwingungsfrequenz beträgt damit f = 1 D
, die Periode T = 2π m .
2π m
D
Berücksichtigt man, daß zur Zeit t = 0 die Schwingung nicht im Nulldurchgang sein muß (anders ausgedrückt, daß der Anfangspunkt der Zeitmessung willkürlich ist), erkennt man, daß
x = x0sin(ωt + ϕ0)
90
auch eine Lösung ist. Dies ist sogar die allgemeine Lösung. ϕ0 heißt die Anfangsphase und
wird im Bogenmaß gemessen. ϕ = ωt variiert während einer Schwingungsperiode von 0 bis
2π. x0 ist die Amplitude der Schwingung. Formal ergeben sich die Konstanten ϕ0 und x0 aus
den Anfangsbedingungen, d.h. der Auslenkung und Geschwindigkeit zur Zeit t = 0.
γ) Das Fadenpendel
Abb. 80: Das Fadenpendel, manchmal auch "mathematisches
Pendel" genannt.
Wenn man von der Bewegungsgleichung (= dem Aktionsgesetz) ausgeht, muß man einmal integrieren, um die Geschwindigkeit zu erhalten. In den meisten Fällen kann man schon diese
Integration nicht wirklich ausführen. Der Energiesatz bringt hier eine große Hilfe, da er v ohne Integration liefert. Als Beispiel wird das Fadenpendel (Abb. 80) betrachtet. Die Differentialgleichung für die Bewegung läßt sich leicht hinschreiben. Da Ft = -mg sinα und der zurück••
gelegte Weg die Bogenlänge ist s = lα, wird die Bewegungsgleichung F t = m s
••
−mg sin α = l α m
und die Differentialgleichung der Bewegung
••
g
α = − sin α
l
Für kleine Winkel gilt die Näherung sinα = α erhält man die gleiche Differentialgleichung wie
bei der harmonischen Schwingung. Es ergibt sich also auch hier eine harmonische Schwingung. Man erhält mit dem gleichen Verfahren wie beim Federpendel
ω 2 = gl ,
T = 2π
g
l
Für große Amplituden ist man auf den Energiesatz angewiesen. Setzt man im Aufhängepunkt
des Fadens Wpot = 0, schreibt sich der Energiesatz
91
-mgl cosα0 = -mgl cosα + mv2/2
v2 = 2gl(cosα - cosα0)
ldα
v kann man auf α umschreiben mit v = ds =
.
dt
dt
dα =
dt
2gl
l
cos α − cos α 0
2g
dα
= dt
l
cos α − cos α 0
t
2g
=∫
l
dα
cos α − cos α 0
Das Integral enthält das Weg - Zeit Gesetz implizit. Dieses kann z.B. durch numerische Integration oder Reihenentwicklung gewonnen werden. Integrale dieser Art definieren elliptische
Funktionen.
Qualitativ kann man aus dem Energiesatz folgern, daß auch bei großen Amplituden noch eine
periodische Schwingung vorliegt. Diese ist allerdings nicht harmonisch, da die Bewegung
nicht durch die Differentialgleichung einer harmonischen Schwingung beschrieben wird.
δ) Anwendung des Energiesatzes bei Anwesenheit von Reibung.
Abb. 81: Im Gebiet (1) wird der Wagen beschleunigt. Im
Gebiet (2) durch die Reibung abgebremst.
Ein Wagen fahre reibungsfrei eine schiefe Ebene hinunter und laufe anschließend waagerecht
aus (Abb. 81). Wie weit kommt er?
Da der Wagen am Anfang und am Ende des Vorgangs ruht, wird seine gesamte anfängliche
potentielle Energie in Reibungsarbeit auf den beiden Streckenabschnitten l und L 2 verbraucht.
Wpot = WR1+ WR2
92
WR1 = FRl = µFNl = µmglcosα = µmgL1
WR2 = FRL2 = µmgL2
mgh = µmgL1 + µmgL2
L2 =
H − µL 1 H
= µ − L1
µ
ε) Wieviel Leistung liefert maximal ein Fluß mit einer Durchflußmenge Q = dm/dt und einem
Gefälle von H?
Ein Massenelement Wasser hat am Anfang des Gefälles die potentielle Energie dmgH. Pro Sekunde liefert der Fluß (dm/dt)gH = QgH an Energie. Diese Leistung steht zur Verfügung.
P = Qmg
Die vollständige Umsetzung setzt voraus, daß am Ende die kinetische Energie des Wassers
verschwindet und daß keine Energie in Wärme umgewandelt wurde.
ζ) Mit welcher Geschwindigkeit fließt eine Flüssigkeit am Boden eines bis zur Höhe H gefüllten Behälters aus?
Betrachte die Gesamtenergie des Systems, bevor und nachdem dm ausgeströmt ist. Die Abnahme der potentiellen Energie ist dmgH, die Zunahme der kinetischen Energie (1/2)dmv2.
Abb. 82: Wie man den Energiesatz bei Strömungsproblemen anwenden kann.
dmgH = (1/2)dmv2
Es folgt die Ausströmgeschwindigkeit
v 2 = 2gH
93
h) Kraft bei mehrdimensionalen Potentialen
Im eindimensionalen Potential, d.h. einem Potential, das nur von einer Ortsvariablen s abhängt, gilt
Fs = −
dW(s)
ds
Bei mehrdimensionalen Potentialen, etwa einem Höhenprofil W(x,y) = mgh(x,y) kann man das
Problem auf das eindimensionaler Potentiale zurückführen, indem man zunächst eine der Ortsvariablen konstant läßt.
Für die Kraftkomponente in x - Richtung erhält man F x = − dW (y bleibt konstant)
dx
dW
Für die Kraftkomponente in y - Richtung
Fy = −
(x bleibt konstant)
dy
∂W
∂x
∂W
Fy = −
∂y
Fx = −
Man schreibt
 Fx 
Der Vektor 
 gibt an jeder Stelle die Richtung des maximalen Gefälles im Potentialge Fy 
birge an (Abb. 85). Man schreibt F = - grad W oder F = −∇W (sprich "Gradient W"). Der
Operator


∇=


∂
∂x
∂
∂y
∂
∂z


 heißt der Nabla - Operator.


Abb. 83: Die Äquipotentiallinien sind die Höhenlinien im
Potentialgebirge. Sie gestatten es, die Größe und Richtung
der Kraft zu ermitteln.
94
6. Das Keplerproblem
a) Historisches
Unter dem Keplerproblem verstehen wir die Aufgabe, bei gegebenen Kraftfeld F =
γmM
2
die
Bahnkurve eines Satelliten r = r(θ) zu bestimmen. Es zeigt sich, daß die Bahnkurve ein Kegelschnitt ist, d.h. je nach Anfangsenergie eine Ellipse, Parabel oder Hyperbel.
Abb. 46 und 85:Satellitenbahnen sind Kegelschnitte.
Die Kepleraufgabe ist nicht nur in der Astronomie von Bedeutung sondern auch für Stöße
zwischen Teilchen, bei denen die Coulombkräfte, für die von der Form her das gleiche Kraftgesetz wie bei der Gravitation gilt, maßgeblich sind. Solche Stöße verwendet man in der
Kernphysik zur Untersuchung der Materie. In der Plasmaphysik bestimmen sie die "Transportphänomene" wie elektrische Leitfähigkeit, Wärmeleitfähigkeit, Diffusion und Viskosität.
Bei bekannten Daten der Planetenbahn (s. Abb.86) (Halbachse a, Exzentrizität ε, Neigung gegen die Erdbahn i, Ausrichtung der Schnittlinie Ω und der Ellipsenachse ω) und bekanntem
Bewegungsablauf, kann die Bahn am Himmel bestimmt werden.
Abb. 86: Bestimmungsgrößen (= Bahnelemente) von
Satellitenbahnen.
Die Bewegung am "Himmel" wird in einem Koordinatensystem dargestellt, das in den Fixsternen verankert ist, dem sogenannten Äquatorialsystem. Die wesentliche scheinbare Bewegung
der Fixsterne kommt durch die Erdrotation zustande (Abb. 87). Die Bahnbewegung der Erde
erzeugt wegen des großen Abstandes der Fixsterne gegen den Bahnradius nur für einzelne
95
Abb. 87: Im Äquatorialsystem haben Fixsterne eine im wesentlichen feste Position. Das Horizontsystem ist im Beobachtungsort fest verankert.
Sterne Abweichungen an der Grenze der Meßmöglichkeit. Wegen der Neigung der Erdachse
gegen die Erdbahn umwandert die Sonne im Laufe eines Jahres am Himmel einen Großkreis,
der gegen den Äquator geneigt ist, die Ekliptik.
Abb. 88 und 89: Die Ekliptik ist der Weg am Himmel, den die Sonne nimmt.
Wenn alle Planetenbahnen in einer Ebene verlaufen würden, würden die Planeten von der Erde aus gesehen auf der Ekliptik entlang wandern (Abb. 90). Dabei ergibt sich beim Überholvorgang eine kurzzeitige rückläufige Bewegung, wie in Abb.90 am Beispiel des Mars demonstriert wird. Wegen der leicht unterschiedlichen Neigungen der Bahnen laufen der Mond und
die Planeten auf einer Straße endlicher Breite entlang der Ekliptik. Während der rückläufigen
Bewegung ergeben sich am Himmel charakteristische Schleifen (Abb.91).
Abb. 90: Erde (innen) und Mars (außen) auf ihren Bahnen.
Der Abstand der Punkte entspricht einem Monat. Die Linien
geben die Blickrichtung an, unter der der Mars von der Erde
erscheint.
Abb. 91: Durch den in Abb. 90 beschriebenen Mechanismus
ergibt sich am Himmel eine schleifenförmige Bahn.
96
Abb. 92: So stellte sich Klaudius Ptolomäus das Zustandekommen der Schleifenbahn vor.
Die Aufgabe der Astronomie bis Kepler bestand darin, diese Scleifenbahnen zu erklären und
vorherzusagen. Bis Kopernikus (1473 - 1543) herrschte das geozentrische Weltsystem vor.
Zur Erklärung der scheinbaren Planetenbahn wurde angenommen, daß sich der Planet auf einem Kreis bewegt, dessen Mittelpunkt wiederum auf einer Kreisbahn um die Erde umläuft.
Die klassische Beschreibung dieses Weltbildes stammt von Klaudius Ptolomäus (70 - 147 n.
Ch.) und ist uns über die Araber im "Almagest" überliefert. Um Unregelmäßigkeiten im Laufe
der Sonne zu verstehen, wird die Erde als außerhalb des Kreiszentrums angenommen, ähnlich
für Mond und Planeten. Aus heutiger Sicht entspricht dies der Approximation der eigentlichen
Ellipsenbahn durch eine exzentrische Kreisbahn. Daß am Himmel der idealen Figur des Kreises gegenüber der Ellipse der Vorzug zu geben ist, war im Altertum selbstverständlich.
Abb. 93: Wie Eratosthenes den Erdradius bestimmte
Es gab bereits im Altertum Ausmessungen des Planetensystems. Eratosthenes (276 - 195
v.Ch.) bestimmte den Erdradius ziemlich genau aus den unterschiedlichen Sonnenhöhen an
verschiedenen gegraphischen Breiten (Abb. 93). Aristarch v. Samos (280 v. Ch.) bestimmte
das Verhältnis Mondbahnradius RM zu Erdbahnradius RS aus dem Winkel zur Sonne bei Halbmond. Hipparch von Niccea (160 - 125 v. Ch.) bestimmte durch Parallaxenmessung, d.h.
durch Bestimmung der Verschiebung des Mondes gegenüber den Fixsternen bei Beobachtung
von verschiedenen Orten der Erde, den Abstand Erde - Mond recht genau zu 59 Erdradien.
Abb. 94: Aus dem Winkel zwischen Sonne und Mond bei
Halbmond läßt sich das Verhältnis der Entfernungen Erde/Mond und Erde/Sonne bestimmen.
97
Mit der gleichen Methode bestimmte er den Sonnenabstand zu 1200 Erdradien. Der wahre
Wert beträgt etwa RS/RE = 24000. Diese Messung war also mit einem Fehler von einem Faktor
20 behaftet, war trotzdem um vieles genauer als alles andere, was es zu der Zeit gab. Die allgemeine Ansicht war, die Sonne befände sich direkt über den Wolken.
Kepler (Johannes Kepler, 1541 - 1630) leitete seine Gesetze aus sehr genauen Beobachtungen
von Tycho Brahe (1546 - 1601) am Planeten Mars her. Tycho Brahe war Hofastronom am
Kaiserhof in Prag, Kepler sein Assistent und späterer Nachfolger. Kepler fand für die Bewegung der Planeten:
Die Planeten bewegen sich auf Ellipsenbahnen, in deren einen Brennpunkt die Sonne
steht.
In gleichen Zeiten werden vom Fahrstrahl gleiche Flächen überstrichen.
a3/T2 ist gleich für alle Planeten. (a ist die große Halbachse der Ellipsenbahn, T die
Umlaufszeit).
b) Einige Eigenschaften von Kegelschnitten
Kegelschnitte sind die Schnittkurven, die man erhält, wenn man einen Doppelkegel mit einer
Ebene schneidet (Abb. 85).
α) Die Ellipse
Abb. 95: Geometrie der Ellipse
Die Ellipse ist die Menge aller Punkte, deren Summe der Abstände zu zwei festen Punkten
konstant ist. Die festen Punkte nennt man Brennpunkte. Mit dieser Definition wird zunächst
die Ellipsengleichung in Polarkoordinaten abgeleitet (s. Abb. 95).
r/ + r = 2a
Nach dem Kosinussatz gilt
also r/ = 2a - r
98
r/2 = r2 + (2εa)2 - 2(2εa)r cosθ
r/ wird ersetzt
(2a - r)2 = r2 + 4ε2a2 - aεar cosθ
4a2 - 4ar + r2 = r2 + 4ε2a2 - 4εar cosθ
a2(1 - ε2) = ar(1 - εcosθ)
1 1 − ε cos θ
r = a(1 − ε 2 )
(12)
ε ist die Exentrizität. Sie läßt sich aus a und b ausdrücken. Nach Abb. 96 gilt
a2 = b2 + (εa)2
b2 = a2(1 - ε2)
(13)
Abb. 96: Zusammenhang von a, b und ε.
In kartesischen Koordinaten gilt
2
x2 + y = 1
2
2
Die Ellipse ist also ein in y - Richtung um den Faktor b/a gestauchter Kreis. Die Fläche wird
durch die Stauchung um den Faktor b/a gegenüber der Kreisfläche reduziert. A = πa2b/a =
πab.
A = πab
99
Damit r im Endlichen bleibt, muß für die Ellipse ε < 1 gelten.
β) Die Hyperbel
Abb. 97: Geometrie der Hyperbel
Die Hyperbel ist die Menge aller Punkte mit konstanter Abstandsdifferenz r/ - r = 2a. Es ergeben sich mit dieser Definition zwei Hyperbeläste. Geht r vom linken Brennpunkt aus und zeigt
auf den rechte Hyperbelast (Abb. 97), so leitet man wie oben bei der Ellipse die Darstellung in
Polarkoordinaten ab. Die funktionale Abhängigkeit r(θ) ist die gleiche wie bei der Ellipse.
Zum Unterschied ist hier ε > 1, und es gibt daher einen gewissen Winkel θ = θa, bei dem r gegen unendlich strebt: cosθa =1/ε. Die Asymptoten bei den Winkeln ±θ a haben die Steigung
tan 2 θ a =
1 − 1 = ε2 − 1 =  b 
(
) a
cos 2 θ
2
Der Scheitelpunkt liegt wie bei der Ellipse im Abstand a vom Zentrum der Figur, der Brennpunkt im Abstand εa. In kartesischen Koordinaten erhält man
2
x2 − y = 1
2
2
γ) Die Parabel
Läßt man in der allgemeinen Polarkoordinatendarstellung ε gegen 1 und a gegen unendlich
gehen, so daß (1 - ε2) konstant bleibt, erhält man eine Parabel (Abb. 98).
r=
p
1 − cos θ
Abb. 98: Die Parabel in Polarkoordinaten. F ist der Brennpunkt.
100
Für θ → 0 geht r → ∞ und tanθ → ∞. Es gibt keine Asymptote.
Einen gedrehten Kegelschnitt erhält man, indem man in der Polarkoordinatendarstellung θ
durch θ - θ0 ersetzt. Nach dem Additionstheorem gilt
cos(θ - θ0) = cosθ cosθ0 + sinθsinθ0
und damit für einen beliebigen Kegelschnitt mit der Abkürzung p = a(1 - ε2)
1 = 1 (1 − ε cos θ cos θ − ε sin θ sin θ)
0
0
r p
Statt der Konstanten ε und θ0, die sich aus den Anfangsbedingungen ergeben, kann man
schreiben
-εcosθ0 = A und -εsinθ0 = B
Wenn man außerdem statt der Konstanten a nach der Definition von p die Konstante p einführt, hat die allgemeine Gleichung eines Kegelschnittes in Polarkoordinaten daher die Form
1 = 1 (1 + A cos θ + B sin θ)
r p
c) Herleitung der Bahngleichung
α) Die Differentialgleichung der Bahn
Wir gehen aus vom
•
Drehimpulssatz
L = mr 2 θ = const
und Energiesatz
1 mv 2 + 1 mv 2 − γmM = E
r
2 r 2 θ
γmM
Bei abstoßenden Kräften würde der das Potential beschreibende Term − r das umgekehrte
Vorzeichen haben. E ist die Gesamtenergie. Im folgenden werden vr und vθ durch r, L und
dr/dθ ausgedrückt.
101
•
dθ
= r/ L 2
v r =r = dr = dr
dt
dθ
dt
•
L
v θ = r θ = r L 2 = mr
(r/ =dr/dθ)
Der Energiesatz hat damit die Form
1 mr /2 L 2 + 1 m L 2 − γmM = E
2 4
2 2
r
2
2
2
r /2 + 1 = 2γm M 1 + 2mE
2
2
2
4
r
Da die Ellipsenbahn besonders einfach in 1/r darzustellen ist, wird transformiert
ρ = 1r
→
ρ /2 + ρ 2 =
dρ
= − 12 dr
dt
r dθ
2γm 2 M
2
ρ + 2mE
2
Die Konstanten auf der rechten Seite werden abgekürzt α =
ρ /2 + ρ 2 = αρ + β
2γm 2 M
2
, β = 2mE
2
(15)
Durch Differenzieren nach θ wird daraus eine lineare Differentialgleichung mit konstanten
Koeffizienten
ρ // + ρ = 1 α
2
(16)
β) Lösung der Differentialgleichung
Man löst eine solche inhomogene Differentialgleichung, indem man zuerst die dazugehörige
homogene Gleichung löst:
ρ// + ρ = 0
mit der allgemeinen Lösung
102
ρ
= ρ0sin(θ - θ0)
= ρ0(sinθ cosθ0 - cosθ sinθ0)
=Bsinθ + Acosθ
und dann eine spezielle Lösung der ursprünglichen inhomogenen Gleichung rät. Hierfür bietet
sich die rechte Seite der inhomogenen Gleichung an. Man geht also mit dem Ansatz
ρ = (1/2)α + Acosθ + Bsinθ
in die Gleichung (16) und stellt fest, daß hiermt die Gleichung gelöst wird. Die Bahnkurve ist
also ein Kegelschnitt.
γ) Abhängigkeit der Bahndaten von E und L
Durch geeignete Wahl der Anfangsrichtung, für die θ = 0 gilt, genügt es von der Lösung
ρ = (α/2) - Bcosθ
(17)
auszugehen. Durch Vergleich mit der Form von Gleichung (12) erkennt man, daß
α
1
ε
=
und B =
2 a(1 − ε 2 )
a(1 − ε 2 )
(18)
Andererseits soll nach Gleichung (15) gelten
ρ /2 + ρ 2 = αρ + β
mit
α=
2γm 2 M
2
und β = 2mE
2
(19)
Wir gehen also mit dem Lösungsansatz Gleichung (17) in diese Gleichung ein, wobei
ρ / = B sin θ = B 2 − B 2 cos 2 θ und ρ /2 = B 2 − B 2 cos 2 θ
Durch das Einsetzen erhält man
103
B 2 − B 2 cos 2 θ +
α2
α2
− αB cos θ + B 2 cos 2 θ =
− αB cos θ + β
4
2
Die linke Seite vereinfacht sich zu
B2 +
α2
− αB cos θ
4
Man erkennt, daß beide Seiten für alle θ übereinstimmen, wenn
B2 +
α2 α2
=
+β
4
2
(20)
Aus Vergleich der Gleichungen (18) und (19) ergibt sich sofort der Gesamtimpuls
2γm 2 M
2
=
2
L
a(1 − ε 2 )
L 2 = a(1 − ε 2 )γm 2 M
(21)
Aus dieser Beziehung ergibt sich das dritte Keplersche Gesetz. Nach dem Flächensatz ist,
wenn jetzt A die vom Fahrstrahl überstrichene Fläche ist,
•
•
A = 1 r2 θ = 1 L
2
2m
•
Da die Fläche der Ellipse AE = πab/T ist, gilt für einen Umlauf A = πab und damit
T
•2
2 2
L 2 = 4m 2 A = 4m 2 a b2 π 2
In Gleichung (21) eingesetzt
2 2 2
4m 2 π a 2 b = a(1 − ε 2 )γm 2 M
(1 - ε2) kann nach Gl. (13) durch die Halbachsen der Ellipse ausgedrückt werden:
1 - ε2 = b2/a2. Dies ergibt
a 3 = γM
T 2 4π 2
104
unabhängig von ε und m.
Setzt man in Gleichung (20) die Beziehungen Gl. (18) ein, erhält man
1
ε2
−
= 2mE
2
2 2
2
2 2
L2
a (1 − ε )
a (1 − ε )
oder
E = −L 2
1
. Setzt man hier L2 aus Gl. (21) ein, ergibt sich für die
2
2ma (1 − ε )
2
Gesamtenergie
E=−
γmM
2a
(22)
Die Gesamtenergie hängt nur von a ab, ist also bei gleichem a unabhängig von der Exzentrizität der Ellipse. Bahnen mit unterschiedlicher Exzentrizität unterscheiden sich im Drehimpuls.
Die Gesamtenergie ebenso die kinetische Energie beim Abstand a sind vom Betrage her halb
so groß wie die negative potentielle Energie im Abstand a. Für alle anderen Abstände verringert sich die kinetische Energie in dem Maße, wie sich die potentielle erhöht (s. Abb. 99).
Abb. 99: Bei der Keplerbewegung hat die kinetische
Energie und die Gesamtenergie den gleichen Betrag.
Um zu berechnen, wo sich ein Körper zu einer vorgegebenen Zeit auf dem Kegelschnitt befindet, dient die Keplersche Gleichung.
Für Hyperbeln, die z.B. beim Stoß gleich geladener Teilchen vorkommen, gilt Gl. (22) mit
positivem Vorzeichen von E.
7. Scheinkräfte
a) Was sind Scheinkräfte ?
Befindet sich ein Fahrer der Masse m in einem mit der Beschleunigung a beschleinigten Fahrzeug, so muß dieses die Kraft F = ma aufbringen, um den Fahrer mit zu beschleunigen. Der
105
Abb. 100: Der Fahrer wird beim Beschleunigen in
die Rücklehne gedrückt. Dies ist eine Scheinkraft.
Fahrer im Auto spürt eine Kraft, die ihn in die Sitzpolster drückt, d.h. im mitbeschleunigten
System scheint eine Kraft F = -ma entgegengesetzt zur Beschleunigung zu wirken. Diese
Kraft braucht man nicht zu berücksichtigen, wenn man den Vorgang von einem unbeschleunigten System aus betrachtet. Man nennt solche Kräfte, die in beschleunigten Bezugssystemen
beobachtet werden, Scheinkräfte. Formal ergibt sich (s. Abb. 101)
Abb. 101: Wenn die Beschreibung der Bewegung von m
von einem Inertialsystem (ex , ey ) aus erfolgt, treten keine
Scheinkräfte auf, aber im beschleunigten System (e*x, e*y)
••
F=m r
r = r∗ + r0
••
••
F = m r 0 + m r∗
•• ∗
mr
••
= F − m r0
(23)
r* beschreibt die Lage der Masse m im beschleunigten Bezugsystem, r0 die Lage des beschleunigten Bezugssystems von einem Inertialsystem aus betrachtet. Gleichung (23) besagt, daß
man in einem beschleunigten Bezugsystem, wenn man in ihm so rechnen will als ob man sich
in einem Inertialsystem befände, zu den tatsächlichen Kräften F die Scheinkräfte
••
F s = −m r 0
hinzuzählen muß. Wenn sich das System mit konstanter Geschwindigkeit bewegt, treten keine
Scheinkräfte auf.
Beispiel
106
In einem beschleunigten Fahrstuhl erhöht sich das Gewicht, wenn die Beschleunigung nach
oben gerichtet ist und erniedrigt sich, wenn die Beschleunigung nach unten weist. Im freien
Fall gilt Fs = - mg. Das scheinbare Gewicht ist daher 0. Der Körper befindet sich in Schwerelosigkeit. Das gleiche würde auch gelten, wenn der Fahrstuhl auf einer Wurfparabel im schrägen Wurf fliegen würde, solange nur die Gravitationskraft wirkt. Eine solche Situation kann
durch den freien (unangetriebenen) Flug einer Rakete auf einer Wurfparabel realisiert werden.
Die Scheinkraft ist auch dann
••
F s = −m r = −mg
und damit entgegengesetzt und vom Betrage her gleich groß wie die Schwerkraft.
Abb. 102: Fällt ein Fahrstuhl frei, so herrscht in ihm
Schwerelosigkeit.
b) Scheinkräfte im rotierenden System
α) Formale Herleitung
Um Scheinkräfte in einem rotierenden System zu berechnen, betrachtet man eine Bewegung,
die im ruhenden System durch r(t) beschrieben wird. Drückt man die Beschleunigung im ruhenden System a durch Beschleunigung a* und Geschwindigkeit v* im bewegten System aus,
•• ∗
so stellt man fest, daß neben a ∗ = x zwei weitere Terme auftauchen, die mit der Masse multipliziert zur Zentrifugal - und Corioliskraft führen.
Wir betrachten zunächst einen beliebigen Vektor G, der sich in einem festen Bezugssystem in
einem Zeitintervall dt um dGfest und in einem mit konstanter Winkelgeschwindigkeit ω rotierenden Bezugssystem gemessen um dGrot ändert.
Abb. 103: dGfest und dGrot sind die Änderungen des Vektors
G vom festen bzw. vom rotierenden System aus gemessen.
dGzus ist der zusätzliche Effekt durch die Rotation.
107
Die Gesamtveränderung ist die, die im festen System gemessen wird. Sie setzt sich aus der
Änderung im rotierenden System dGrot und der zusätzlichen Änderung durch die Rotation
dGzus zusammen (Abb. 103).
dGfest = dGrot + dGzus
Die Änderung durch die Drehung ergibt sich nach Abb. 104 aus
dG zus = dϕ × G
Abb. 104: Der Zusammenhang von dϕ und dGzus.
Division durch dt und Berücksichtigung von ω =
dϕ
ergibt
dt
 dG  =  dG  + ω × G
 dt  fest  dt  rot
(23)
G kann ein beliebiger Vektor sein, der sowohl im ortsfesten wie im rotierenden Koordinatensystem dargestellt werden kann. Für einen körperfesten Vektor gilt z.B.
 dG  = 0
 dt  rot
→
Für einen raumfesten Vektor G
 dG  = 0 →
 dt  fest
 dG  = ω × G
 dt  fest
 dG  = −ω
ω×G
 dt  rot
Für G = r erhält man die Transformation der Geschwindigkeiten
 dr  =  dr  + ω × r
 dt  fest  dt  rot
Da  dr  = v und  dr  = v ∗ die Geschwindigkeiten im festen bzw. im rotierenden Bedt fest
dt rot
zugssystem sind, erhält man als Transformation der Geschwindigkeiten
v = v ∗ + ω×r
(24)
108
Gleichung (23) gilt auch, wenn man für G v einsetzt. Dies liefert uns die gewünschte Transformation der Beschleunigungen.
 dv  =  dv  + ω × v
 dt  fest  dt  rot
In den beiden Termen auf der rechten Seite wird v aus Gleichung (24) eingesetzt. Die Ableitungen der Geschwindigkeiten sind die Beschleunigungen im festen bzw. im rotierenden System. Es folgt
∗
a =  dv 
dt
+ ω ×  dr 
dt
+ ω × v ∗ + ω × (ω × r)
= a ∗ + 2ω × v ∗ + ω × (ω × r)
Neben der Beschleunigung im rotierenden System a* erscheinen rechts zwei Terme von der
Dimension einer Beschleunigung, die multipliziert mit der Masse die Scheinkräfte ergeben.
Rechnet man also im rotierenden System so, als ob es ein Inertialsystem wäre, muß man die
Scheinkräfte
F z = −mω × (ω × r) = m(ω × r) × ω
und
F c = −2mω × v = 2mv × ω
zu den wahren Kräften addieren.
β) Die Zentrifugalkraft
Die Kraft
F z = m(ω × r) × ω = mv × ω
ω hat radiale Richtung
Abb. 105: v×ω
109
ist die Zentrifugalkraft. Sie zeigt radial nach außen und hat den Betrag mrω2. Bei der rotierenden Erde ist die Zentrifugalkraft von der geographischen Breite λ abhängig. Nimmt man für
die Erde die Gestalt einer Kugel mit dem Radius R an, so hat man
Fz = mRω2cosλ
Die Resultierende von Fz und der Schwerkraft FG ist die Gesamtkraft auf ein Teilchen an der
Oberfläche der Erde. Solange sie eine Komponente parallel zur Oberfläche hat, werden sich
Teilchen entlang der Oberfläche verschieben. Das nimmt erst dann ein Ende, wenn sie genau
senkrecht zur Oberfläche steht. Die Erdoberfläche hat daher nicht Kugelgestalt sondern die
Gestalt einer abgeplatteten Kugel (eines Geoids) wie übertrieben in Abb. 106 dargestellt.
Abb. 106: Die Gesamtkraft auf ein Teilchen an der Erdoberfläche ist FG + Fz im rotierenden System. Die Erdoberfläche stellt sich senkrecht zu dieser Kraft ein, da eine Verschiebung des Teilchens möglich ist.
Die senkrecht zur Oberfläche wirkende Komponente der Zentrifugalkraft Fz cosλ führt zu einer Verringerung der effektiven Gravitationskraft. Man sieht, daß man die Diskussion der
Kraftverhältnisse an der Erdoberfläche vom ruhenden System aus betreiben kann, wie wir es
im Kapitel C.3.h gemacht haben, oder vom bewegten System aus, wobei als Zusätzliche Kräfte Scheinkräfte eingeführt werden müssen. Die Schlußfolgerungen sind die gleichen. Ähnlich
kann man die für Kurvenfahrt optimale Neigung der Fahrbahn anschaulich sehr bequem mit
der Zentrifugalkraft diskutieren (Abb. 107). Man sagt, die Neigung der Fahrbahn muß so sein,
daß die Resultierende aus Gewichtskraft FG und Zentrifugalkraft senkrecht zur Fahrbahn
stehen.
Abb. 107: Ähnlich wie beim Geoid muß bei der Kurvenfahrt die Resultierende Kraft senkrecht auf der Fahrbahn
stehen.
110
γ) Die Corioliskraft
i. Woher kommt die Corioliskraft?
Die Corioliskraft tritt nur bei Körpern auf, die sich vom rotierenden System aus gemessen bewegen. Man macht sich ihre Ursache am besten durch einen Wurfversuch am Nordpol klar,
wo die Drehachse senkrecht zur Erdoberfläche steht (Abb. 108).
Abb. 108: Der Mittelpunkt des Kreises ist der Nordpol. Im
Abstand ρ wird ein Stein radial nach außen geworfen. Durch
die Eigenbewegung der Erde erhält er eine azimutale Geschwindigkeitskomponente. Diese ist kleiner als die am
Zielpunkt.
Ein mitrotierender Schütze würde sein Ziel verfehlen, da er dem Geschoß eine seitliche Anfangsgeschwindigkeit v = ρω durch die Erddrehung mitliefert, und das Ziel im Abstand r sich
bei der Rotation schneller (V = ωr) bewegt als der Schütze im Abstand ρ < r. Das Ziel hat sich
in der Zeit ∆t von A nach B bewegt, das Geschoß von A nach C. Die seitliche Abweichung
vom Ziel ist also
s = AB - AC = rω∆t - ρω∆t = (r -ρ)ω∆t
(r - ρ) kann durch die Geschwindigkeit in Abschußrichtung v0 ausgedrückt werden. Wenn
man annimmt, daß die seitliche Bewegung sehr klein gegen die in Schußrichtung ist, erhält
man
(r - ρ) = v0∆t
s = v 0 ω∆t 2
Vergleicht man dieses Ergebnis mit dem Weg - Zeit - Gesetz einer Bewegung mit konstanter
Beschleunigung, so erkennt man, daß die seitliche Bewegung im rotierenden System mit konstanter Beschleunigung ac = 2v0ω verläuft. 2v0ω ist der Betrag der Beschleunigung, den wir
111
von der Corioliskraft her erwarten. Bei bei beliebiger geographischer Breite gibt es eine vertikale und eine horizontale Komponente der Corioliskraft.
ii. Corioliskraft bei horizontaler Bewegung
Abb. 109: Nur ω⊥ führt zu einer Beeinflussung der horizontalen Bewegung.
Man zerlegt ω in eine vertikale und eine horizontale Komponente (Abb. 109). Die Horizontalkomponente bewirkt eine senkrechte Kraft, die bei Bewegung auf einer Unterlage keinen Einfluß auf den Bewegungsablauf hat. ω⊥ steht immer senkrecht auf v und erzeugt eine konstante
Beschleunigung 2v×ω
ω.
Abb. 110: ω⊥ steht immer senkrecht auf v.
Es resultiert wie beim Elektron im Magnetfeld eine Kreisbewegung. Am Äquator ist ω⊥ = 0
und damit ac = 0. Auf der Nordhalbkugel ergibt sich immer eine Ablenkung nach rechts, auf
der Südhalbkugel nach links. Dies führt zu den charakteristischen Wirbeln in der Bewegung
von Luft und Wasser, die auf der Nord - und Südhalbkugel umgekehrten Drehsinn haben.
Abb. 111: Der Umlaufsinn des Windes in Hoch- und Tiefdruckgebieten rührt von der Corioliskraft her.
iii. Corioliskraft bei vertikaler Bewegung
Bei vertikaler Bewegung bewirkt die parallel zur Oberfläche stehende Komponente von ω,
ω// = ωcosλ eine geringfügige seitliche Ablenkung. Beim freien Fall ist diese immer nach
Osten gerichtet (s. Abb. 112). Für die Berechnung der seitlichen Ablenkung gehen wir genau
112
wie oben bei der Betrachtung des Schusses am Nordpol davon aus, daß die Bewegung nur wenig gestört wird und daher die Geschwindigkeit, die man in der Formel für die Corioliskraft
einsetzen muß, die ungestörte Geschwindigkeit des freien Falls ist.
vy = gt
Fc = 2mω//v = 2mωcosλ = 2mgωt cosλ = m(dvx/dt)
vx = gωcosλ t2
Nach Integration erhält man
3
x = gω(cos λ) t
3
Abb. 112: Auch auf einen Körper im freien Fall wirkt die
Corioliskraft.
113
KAPITEL D
Dynamik von Massenpunktsystemen
1. Der Massenmittelpunkt
a) Das Hebelgesetz
Unter dem Schwerpunkt von zwei starr verbundenen Massen versteht man den Punkt der Verbindungslinie, bei dem das System unterstützt werden muß, um im Gleichgewicht zu bleiben.
Abb. 113: Bei symmetrischen Körpern liegt der Schwerpunkt
in der Mitte.
Wir vermuten, der Schwerpunkt unterteilt die Verbindungslinie im Verhältnis der Massen,
wobei der kürzere Teil der Verbindungslinie neben der größeren Masse liegt. Man nennt diesen Satz auch das Hebelgesetz. Das Hebelgesetz war schon im Altertum bekannt. Nach Archimedes kann man es ableiten, wenn man annimmt, daß bei gleichen Massen der Schwerpunkt
in der Mitte der Verbindungslinie liegt.
Abb. 114: Nach Archimedes kann man das Hebelgesetz für rationale Verhältnisse aus dem symmetrischen Fall (Abb. 113)
herleiten.
Man teilt die Masse m1 (s. Abb. 114) in zwei gleiche Teile und schiebt sie außeinander so daß
ihr Schwerpunkt fest bleibt und eine Hälfte auf dem Unterstützungspunkt liegt. Diese trägt
dann nicht mehr zum Gleichgewicht bei und kann auch entfernt werden. Da der Schwerpunkt
der beiden Teilmassen von m1 an seinem Ort geblieben ist, herrscht nach wie vor Gleichgewicht. Damit ist das Hebelverhältnis 2 : 1 bei einem Massenverhältnis 2 : 1 bewiesen. Durch
Aufteilung der Masse m2 im Verhältnis 2 : 1 und Anwendung des im ersten Schritt bewiesenen Satzes beweist man das Hebelverhältnis 2 : 3 und so durch geschickte Aufteilung der
Massen für alle rationalen Verhältnisse.
Heute leitet man das Hebelgesetz am einfachsten aus dem Energiesatz her. Man denkt sich eine massenfreie Stange, an deren beiden Enden die Kräfte m1g und m2g angreifen. Die Stange
werde an dem Punkt unterstützt, der zu einem Gleichgewicht führt. Kippt man die Stange so,
114
Abb. 115: Rechts und links muß nach dem Energiesatz
gleche Arbeit geleistet werden.
daß das eine Ende um die Strecke s1 verrückt wird, so leistet die Kraft m1g eine Arbeit m1gs1.
Da sich jedes Teilchen der gesamten Anordnung in einem Potentialfeld aufhält, gilt der Energiesatz und damit m1gs1 = m2gs2. Wegen des Strahlensatzes hängen die Verschiebungen der
Enden von den Längen der Teilarme des Hebels ab (Abb.117): s1/s2=l1/l2, und daher
m1 l2
m2 = l1
Wer sagt es denn!
Da g im Prinzip von der Position auf der Erde und damit von x abhängig ist, könnte man
streng genommen zwischen Schwerpunkt, beschrieben durch die Koordinaten x1
(s)
und x2
(s)
vom Schwerpunkt aus gerechnet
m1gx1(s) + m2gx2(s) = 0
und dem Massenmittelpunkt, gekennzeichnet durch die Position
m1x1(MM) + m2x2(MM) = 0
(1)
Unterscheiden. x1(MM) und x2(MM) sind die Koordinaten der beiden Massen vom Massenmittelpunkt gemessen. Im folgenden wird auf diese Unterscheidung keinen Wert gelegt. Wir meinen
den Massenmittelpunkt, wenn wir Schwerpunkt sagen.
b) Der Schwerpunkt beliebiger Massenpunktsysteme
Auf n Massen verallgemeinert lautet die Definition des Schwerpunktes nach Gleichung (1)
Σ m i x (s)i = 0
entsprechend für die anderen Koordinaten
Σ m i y (s)i = 0 und Σ m i z (s)i = 0
115
n
allgemein
Σ= m i r (s)i = 0
Diese Definition hat die etwas unbequeme Eigenschaft, daß sich der Koordinatenursprung,
von dem aus die Positionen der Massen gemessen werden, im Schwerpunkt befinden muß.
Um eine Definition für ein beliebiges Koordinatensystem zu erhalten, betrachten wir Abb.
116. ri ist die Position der Masse i von diesem Koordinatensystem aus. rs die Position des
Schwerpunktes. Dann gilt laut Abb. 116
ri = ri(s) + rs
Σ m i (r i − r s ) = 0
Σ m i r i = Σ m i r s = r s m ges
mges ist die Gesamtmasse des Systems. Damit erhält man für die Position des Schwerpunktes
Σmr
rs = m i i
ges
(2)
Abb. 116: Die geometrischen Verhältnisse bei der Berechnung
des Schwerpunktes.
c) Schwerpunkt als Mittelwert der gewichteten Massenpositionen
Gleichung (2) hat die Form einer gewichteten Mittelwertbildung. Betrachtet man z.B. die Körperlänge einer Gruppe von Studenten. mi Studenten mögen die Länge ri haben. Dann ist der
Mittelwert
r=
Σ miri
Σ mi
116
mi ist gewissermaßen das Gewicht, mit dem jede Länge berücksichtigt wird. Ein demokratischer Mittelwert ist das arithmetische Mittel.
Man kann auch bei anderen Mittelwertbildungen ein gewichtetes Mittel einführen. Es sei z.B.
bei einer Entscheidung über eine quantifizierbare Größe, etwa die Note für eine Leistung, die
Meinung des Studenten MS, die Meinung des Professors MP. Dann erhielte man bei demokratischer Mittelwertbildung
MD =
MS + MP
2
Wichtet man mit der Kompetenz der Parteien, hätte ein gewichtetes Mittel die Form
MG =
mSMS + mPMP
m +m
Abb. 117: Die Formel für den Schwerpunkt ist die Gleiche
wie diejenige die man üblicherweise zur Bildung des gewichteten Mittelwertes anwendet
d) Schwerpunkt kontinuierlicher Massenverteilungen
α) Der Übergang von diskreten zu kontinuierlichen Massen
Für Künstler, die komplizerte Skulpturen schaffen, ist die Lage des Schwerpunktes eine wesentliche Größe. Der Schwerpunkt sollte im allgemeinen oberhalb der Fläche liegen auf der
die Statue unterstützt wird. Um die Lage des Schwerpunktes abzuschätzen, unterteilt man die
gesamte Figur in Teilelemente, deren Masse ∆mi und Schwerpunktslage ri man abschätzen
kann, etwa in Abb. 118 das Schwert, den Unterarm, den Oberarm u.s.w.. Die Lage des
Schwerpunktes ergibt sich aus
Abb. 118: Bei unregelmäßigen Körpern kann man in der
Praxis als dm Massenelemente beträchtlicher Ausdehnung
nehmen, z.B im abgebildeten Fall die Hand, das Schwert,
den Kopf.
117
rs =
Σ r i ∆m i
m ges
Im Grenzfall ∆m → 0
∫ rdm
rs = m
ges
Abb. 119: dm bei einer eindimensionalen Massenverteilung
β) Das Massenelement
Um uns klar zu werden, was dm bedeutet, betrachten wir eine eindimensionale Massenverteilung wie in Abb. 119. Wir können uns etwa einen Löffel vorstellen, bei dem wir letztendlich
die Lage seines Schwerpunktes in seiner Längsrichtung ermitteln wollen. m(x) ist die Masse
vom Anfang des Löffels bis zur Position x. ∆m ist dann die Masse zwischen den Positionen
m(x) und m(x + ∆x)
∆m = m(x + ∆x) − m(x) = m(x) + dm ∆x − m(x) = dm ∆x
dx
dx
m(x + ∆x) wurde dabei einer Taylorentwicklung bis zum ersten Gliede unterzogen. dm/dx = ρ
heißt die Massenbelegung oder die Liniendichte. Entsprechend gibt es dm/dA die Flächendichte und dm/dV die Volumendichte. Die Verteilung der Masse wird also praktischerweise nicht
durch m(x) sondern ρ(x) dargestellt. Wenn ρ unabhängig von x ist, spricht man von einem homogenen Körper. Ähnlich wird bei Geschwindigkeitsverteilungen von Teilchen nicht die Zahl
der Teilchen mit der Geschwindigkeit v, N(v), dargestellt, sondern die Anzahl der Teilchen
deren Geschwindigkeit zwischen v und v + dv liegt: ∆N = f(v)∆v. Für ∆v → 0 geht auch
∆N → 0. Kein Teilchen hat nämlich mit beliebiger Genauigkeit irgend eine vorgegebene Geschwindigkeit. Der Schwerpunkt eines kontinuierlichen Körpers ergibt sich also aus
rs =
∫ rdm
∫ dm
Für einen homogenen Körper mit konstanter Dichte ρ und dm = ρdV
rs =
∫ rdV = ∫ rdV
V
∫ dV
(3)
118
V ist das Volumen des Körpers. Die Gl. (3) enthält drei Gleichungen für die drei kartesischen
Koordinaten des Schwerpunktes.
Abb. 120: Zuerst summiert man über alle Volumenelemente bei festgehaltenen zwei Koordinaten und laufender
dritten.
γ) Wie berechnet man Volumenintegrale?
Einen geometrisch einfachen Körper kann man durch Integration behandeln. Dazu unterteilt
man ihn in Teilmassen, indem man ihn mit einem Koordinatengitter durchsetzt, so daß für einen Schnitt eine Koordinate, z.B. ξ konstant gehalten wird. der benachbarte Schnitt läuft dann
bei ξ + ∆ξ. In kartesischen Koordinaten (s. Abb. 120) hat man Volumenelemente
∆V = ∆x∆y∆z. In Zylinderkoordinaten, in denen die Position durch r,θ,z beschrieben wird, ist
das Volumenelement ∆V = r∆r∆θ∆z (s. Abb. 121). Wer es nicht glaubt, berechne ein Würfelvolumen auf der Erdoberfläche, indem er dieses durch den Erdradius, die geographische Breite und eine Koordinate ∆z in Ost - West Richtung ausdrückt!
Abb. 121: Das Volumenelement in Zylinderkoordinaten.
Man summiert, indem man zuerst zwei Koordinaten konstant läßt, z.B. in kartesischen Koordinaten x und y. Es ergibt sich der Schwerpunkt für eine Reihe von Volumenelementen. Er
hängt natürlich von dem speziell gewählten xi und yj ab (Abb. 120). Im allgemeinen ergibt sich
eine Funktion von x und y, so daß man nach diesem Schritt den Schwerpunkt für jede der Reihen, die durch ein bestimmtes i und j gekennzeichet sind (i, j = 1,2, ....), kennt.
rs = 1
V
Σi Σj  Σk r i (x, y, z)∆z  ∆x∆y = V1 Σi Σj r(x, y)∆x∆y
119
Abb. 122: Bei der nächsten Integration summiert man über
alle Volumenelemente einer Scheibe.
Als nächstes läßt man eine der übrigen Koordinaten konstant, z.B. y und erhält den Schwerpunkt jeder Scheibe (Abb. 122).
rs = 1
V
Σ r(x)∆x
Die letzte Summation ergibt den Schwerpunkt. Im Grenzübergang wird aus aus jeder Summation eine Integration
rs = 1
V
∫ ∫ ∫ rdxdydz
(4)
Man löst dieses sogenannte Volumenintegral, indem man wie bei der Summation nur eine Koordinate variabel läßt. Die Integrationsgrenzen sind durch die Körperform bestimmt und hängen im allgemeinen von den noch nicht abgearbeiteten Variabeln ab.
Beispiel: Schwerpunkt einer homogenen Dreiecksfläche konstanter Dicke d.
Abb.123: Berechnung des Schwerpunktes eines Dreiecks
Das allgemeine Dreieck kann wie in Abb. 123 aus rechtwinkligen Dreiecken zusammengesetzt werden. Daher wird im folgenden nur ein rechtwinkliges Dreieck in dem dafür bequemsten Koordinatensystem berechnet. Nach Gleichung (4) gehen wir von der Formel aus
xs =
1
1
∫ ∫ ∫ xdxdydz
bhd
120
erster Schritt: x und y sind konstant
d 
x s = 2 ∫ ∫  ∫ dz  dxdy = 2
bhd
bh
 0 
∫ ∫ xdxdy (das Integral in der Klammer ergibt d)
zweiter Schritt: x wird konstant gelassen
0 
x s = 2 ∫  ∫ dy  xdx
bh 

y
y0
Hierin ist
∫ dy = y 0 = b x
h
Die obere Grenze ist durch die Berandung des Körpers gegeben und hier von x abhängig. Die
letzte Integration ergibt dann die Lage des Schwerpunktes in x Richtung.
x s = 22
b
b
2 b3 = 2 b
2
=
x
dx
∫
b2 3 3
Die Lage des Schwerpunktes in y - Richtung ergibt sich mit der gleichen Betrachtung, in z Richtung ist die Lage trivialerweise xz = d/2. Bei der letzten Integration müssen alle möglichen
Werte der letzten Variablen ausgeschöpft werden. Z.B. wäre bei der Integration über den Quadranten eines Kreises
y0 = R2 + x2
Bei der Integration über x wären die Grenzen 0 und R.
Abb. 124: Die Grenzkurve eines Kreisquadranten
δ) Experimentelle Bestimmung der Lage des Schwerpunktes
Außerhalb des Schwerpunktes aufgehängte Körper hängen so, daß der Schwerpunkt unterhalb
des Unterstützungspunktes liegt. Der Schwerpunkt liegt also auf einer Geraden, die durch den
121
Abb. 125: Wie man die Lage des Schwerpunkts eines Autos in horizontaler Richtung bestimmen kann.
Unterstützungspunkt geht und vertikale Richtung hat. Durch Aufhängen an zwei unterschiedlichen Unterstützungspunkten erhält man zwei Geraden, in deren Schnittpunkt der Schwerpunkt liegt. Wenn ein Körper nicht bequem aufgehängt werden kann wie etwa ein Auto, kann
man auch folgenderweise vorgehen: Man wiegt das Fahrzeug an der Hinterachse, indem man
es auf der Vorderachse aufliegen läßt und an der Hinterachse auf eine Waage stellt. Das Gewicht sei dann FH. Entsprechend wiegt man es unter der Vorderachse. Das entsprechende Gewicht sei FV. Anwendung des Hebelgesetzes ergibt
FHL = Mgs
FVL = Mg(1-s)
Durch Division der beiden Gleichungen erhält man
FV  1
=  s − 1 
F
und damit l = F V + 1,
s FH
s=lF 1
V
+1
FH
FHl FH  FV
= g
+ 1
M = sg
 FH

2. Bewegung des Schwerpunktes
a) Das Aktionsgesetz
Auf ein System von Teilchen wirken äußere Kräfte F1, F2, ...und innere Kräfte, d.h. irgendwelche Wechselwirkungen zwischen zwei Teilchen des Systems, F12, F21, F13, ...Für jedes
Teilchen gilt das Aktionsgesetz
•
m 1 v 1 = F 1 + F 12 ...
122
Abb. 126: Zwei Massen unter dem Einfluß von inneren und
äußeren Kräften
•
m 2 v 2 = F 2 + F 21 ...
...
Die Gleichungen für alle Teilchen werden rechts und links addiert. Dabei heben sich nach der
Regel actio = reactio alle inneren Kräfte heraus, da es zu jeder Kraft eine gleich große entgegengesetzte gibt: F12 = - F21. Man erhält also
Σ m i v i = Σ F ext
•
Die linke Seite kann man mit Hilfe der Definition des Schwerpunktes (Gleichung (2)) um•
•
•
schreiben, denn aus x s m ges = Σ m i x i folgt durch Differentiation v s m ges = Σ m i v i . v s ist die
Beschleunigung des Schwertpunktes.
m ges v s = Σ F ext
•
(5)
Der Schwerpunkt eines Systems von Massen bewegt sich unter einer äußeren Kraft so, als ob
die gesamte Masse im Schwerpunkt vereinigt wäre. Ohne äußere Kraft bewegt sich also der
Schwerpunkt mit konstanter Geschwindigkeit. Bei einer Explosion fallen die Einzelteile nach
allen möglichen Richtungen auseinander, aber der Schwerpunkt bleibt - zumindest solange die
Splitter frei fliegen - an der Stelle, an der der explodierende Körper anfangs gestanden hatte.
b) Das Zweikörperproblem, reduzierte Masse
Bewegen sich zwei Körper unter der gegenseitigen Wechselwirkung, etwa wie die Erde um
die Sonne, so ist die äußere Kraft null und der Schwerpunkt ruht in einem Inertialsystem. Die
Kraft auf jeden Körper hat die Richtung der Verbindungslinie der beiden Körper und zeigt daher immer auf den Schwerpunkt. Man kann daher die Bewegung durch eine Zentralkraft, die
vom Schwerpunkt ausgeht, beschreiben. Das Problem ist auf das Keplerproblem zurückgeführt. Die Körper bewegen sich auf Kegelschnitten um den Schwerpunkt. Würde man das Koordinatensystem in den Schwerpunkt eines der beiden Körper legen, dürfte das Aktionsgesetz
nicht ohne weiteres als Grundlage der Beschreibung verwendet werden, da hierfür das
123
Abb. 127: Zur Definition der reduzierten Masse
zugrundegelegte Koordinatensystem ein Inertialsystem sein müßte. Formal kann man die Bewegung auch in einem Koordinatensystem, das im Zentrum der Sonne verankert ist, beschreiben. Man muß dann allerdings statt der wahren trägen Masse des umlaufenden Körpers seine
reduzierte Masse µ nehmen, die im folgenden erläutert wird.
Zunächst wird die Relativgeschwindigkeit v12 = v1 - v2 eingeführt (s. Abb. 127). Für jeden
Körper einzeln gilt
•
F
v 1 = m12
1
•
F 21
v2 = m
2
Durch Subtraktion beider Gleichungen erhält man mit der Bedingung F12 = - F21
•
•
•
v 12 =  v 1 −v 2  = F 12  m1 + m1 
1
2
1 = 1 + 1 , wobei µ die reduzierte Masse ist, lautet die BewegungsgleiMit der Definition µ
m1 m2
chung dann
•
µ v 12 = F 12
Sie enthält die Beschleunigung von einem der beiden Körper aus gemessen, die wahre Anziehungskraft - d.h. für das Gravitationsgesetz ist die wahre Masse einzusetzen - und als träge
Masse die reduzierte Masse.
Beispiel: System Proton - Elektron
memp
me
me 
1
1

m p = 1840 µ = m e + m p = m e 1 + m e ≈ m e  1 − m p 
mp
D.h. man kann so rechnen, als ob das Proton unbeweghlich im Zentrum steht, das Elektron
aber eine um 0,06% verminderte träge Masse hätte.
124
3. Dynamische Hilfsbegriffe
a) Der Impuls
Nach Definition des Schwerpunktes gilt
r s = m1
ges
und daher
Σ miri
m ges r s = Σ m i r i = Σ p i = p ges
•
•
Die Summe aller Einzelimpulse ist genau so groß wie der Impuls der Gesamtmasse im
Schwerpunkt des Teilchensystems. Bezogen auf den Schwerpunkt ist der Gesamtimpuls
p ges = mgesvs = 0.
b) Der Drehimpuls
α) Die Bewegungsgleichung für Rotation
Wir haben wieder ein Teilchensystem mit den Massen m1, m2, u.s.w. auf die äußere Kräfte Fi
und innere Kräfte Fik wirken. Der Gesamtdrehimpuls L bezüglich eines beliebigen Bezugspunktes ist die Summe der Drehimpulse der Einzelteilchen.
L = L 1 + L 2 + ... = r 1 × p 1 + r 2 × p 2 ...
Für die einzelnen Drehimpulse gilt nach dem Aktionsgesetz für Drehungen (Kap. C.4.a)
•
L 1 = r 1 × F 1 + r 1 × F 12 + ...
•
L 2 = r 2 × F 2 + r 2 × F 21 + ...
Durch Addition erhält man
•
L = r 1 × F 1 + r 2 × F 2 + (r 1 − r 2 ) × F 12 + ...
Bei Zentralkräften ist F12 parallel zu (r1 - r2) und damit das durch F12 bewirkte Drehmoment
Null. D.h., wenn alle inneren Kräfte Zentralkräfte sind, gilt bezüglich eines beliebigen Drehpunktes in einem Inertialsystem
125
•
(6)
L = M ext
Die Änderung des Gesamtdrehimpulses ist also nur durch die externen Drehmomente bestimmt. Beim Fehlen äußerer Kräfte bleibt L konstant. Der Drehimpulssatz gilt im allgemeinen nur für ein Inertialsystem. Beschreibt man die Bewegung aber vom Schwerpunkt aus, so
gilt der Drehimpulssatz auch, wenn der Schwerpunkt beschleunigt wird. Um dies zu beweisen,
drückt man den Drehimpuls L in einem Inertialsystem und das gesamte Drehmoment der äußeren Kräfte durch entsprechende Größen im Schwerpunktsystem aus, indem man
transformiert
ri = rs + ri(s)
Abb. 128: Transformation in das Schwerpunktsystem
(s. Abb.128). ri ist der Ortsvektor des iten Teilchens in einem Inertialsystem, ri(s) der im
Schwerpunktssystem. Die Bewegung des Schwerpunktes, die nicht geradlinig, gleichförmig
zu verlaufen braucht, bezeichnet man als Translation. Mit obiger Transformation ergibt sich
L = Σ ri × p i = Σ rs × p i + Σ ri × p i
(s)
Die beiden Terme auf der rechten Seite lassen sich vereinfachen
Σ r s × p i = r s × Σ p i = r s × p ges
Σ r (s)i × p i = Σ r (s)i × m i r s + Σ r (s)i × p (s)i
•
•
(s)
(s)
da p i = m i r s + p i . Andererseits ist nach Definition des Schwerpunktes  Σ r i m i  × r s = 0
also
Σ r (s)i × p i = Σ r (s)i × p (s)i
126
Der Gesamtdrehimpuls von einem Inertialsystem aus gesehen besteht also aus einem Drehimpuls des Schwerpunktes L s = r s × p ges = m ges r s × v s und einen Drehimpuls um den Schwerpunkt L (s) =Σ r i × p i
(s)
(s)
L = L s + L (s) = r s × p ges + Σ r i × p i
(s)
(s)
(7)
Ebenso gilt für das Drehmoment
M ext = M s + M (s)
wobei M s = r s × F ext das Drehmoment der äußeren Kräfte bezüglich des Koordinatenur(s)
sprungs und M = Σ r i × r i bezüglich des Schwerpunktes ist. Nach Gleichung (6) gilt
M ext = dL . Setzt man hier Gleichung (7) ein, erhält man
dt
(s)
•
•
• (s)
M ext = r s × p ges + r s × p ges +L
•
•
•
•
da r s × p ges = m ges r s ×r s = 0 und r s ×p s = r s × F ges = M s , andererseits M ext = M s + M (s) gilt
hier
• (s)
M (s) =L
wie anfangs behauptet. Die Gesamtbewegung eines Körpers kann also immer als Überlagerung einer Translation des Schwerpunktes und einer "Rotation" um den Schwerpunkt aufgefaßt werden, wobei man sich unter einer Rotation hier nicht unbedingt die Drehung eines starren Körpers vorstellen muß, sondern eine beliebige Bewegung der verschiedenen Punktmassen von einem Koordinatensystem aus gemessen, das im Schwerpunkt ruht. Für die Translation ist die Summe der äußeren Kräfte, für die Rotation die Summe der äußeren Drehmomente
bezüglich des Schwerpunktes verantwortlich. Die inneren Kräfte haben auf die Größe Ls und
pges keine Auswirkung.
β) Anwendungen
Bei Fehlen äußerer Drehmomente bleibt der Gesamtdrehimpuls erhalten. Aus diesem Grund
benötigt ein Hubschrauber einen Drehmomentenausgleich durch einen seitlichen Propeller
oder einen zweiten Rotor. Bei einem sich zusammenziehenden Stern (oder in ein Ausflußloch
127
fließendem Wasser) nimmt die Winkelgeschwindigkeit bei der Kontraktion zu, denn da L konstant ist und L = mr2dθ/dt gilt, muß dθ/dt zunehmen, wenn im Mittel r kleiner wird. Im freien
Fall können Turmspringer oder Katzen den Gesamtkörper drehen ohne äußere Drehmomente.
Im Prinzip ist dies bei der Katze möglich durch Drehen des Schwanzes. Messungen haben ergeben, daß dieser Mechanismus die Geschwindigkeit, mit der Katzen sich drehen, nicht erklären kann.
Abb. 129: Es gibt verschiedene Möglichkeiten für die Katze, durch innere Kräfte ihren Körper zu drehen.
Ein Modell für die Katzenrolle ist das Abrollen zweier Zylinder mit Kegelspitzen (Abb. 129).
Die Abrollbewegung ist durch innere Kräfte möglich. Dadurch ergibt sich ein Drehimpuls in
den Achsen der Zylinder und ein entgegengesetzter Drehimpuls des Gesamtkörpers.
Teilchen haben einen Spin, den man sich mechanisch als Drehimpuls um die Körperachse vorstellt. Der Drehimpuls hat die Dimension
[L] = [mrv] = kgm 2 s −1 = Js
Größen der Dimension Js (Wirkung) sind gequantelt, d.h. es gibt kleinste Portionen. Der
kleinste vorkommende Drehimpuls ist 1/2h, wobei h = 10-34Js. Der Spin eines Teilchens ist daher ebenfalls gequantelt. Wegen der Quantelung von Drehimpulsen können sich diese bei
zwei Teilchen nur so addieren, daß wieder ein Vielfaches des Elementarquantums herauskommt. Ein System aus zwei Teilchen mit dem Einzeldrehimpuls (1/2)h (Spin 1/2) hat also
den Spin 0 oder 1. Der Spin hat für jedes Teilchen einen fest vorgegebenen Wert. Es gibt Teilchen mit ungeradzahligem Spin (1/2, 3/2, ...) (Fermionen), und geradzahligem Spin (Bosonen). Fermionen und Bosonen zeigen besonders hinsichtlich ihrer Statistik stark unterschiedliches Verhalten. Die Drehimpulserhaltung schließt gewisse Zerfälle aus. Beim Beta Zerfall eines Neutrons hatte man zunächst nur ein Proton und ein Elektron entdeckt. Da beide
Teilchen einen Spin 1/2 haben, zusammen also einen geradzahligen Spin aufbringen, das Ausgangsteilchen einen Spin 1/2 hat, wurde die Beteiligung eines weiteren Teilchens mit Spin 1/2
128
gefordert, um die Drehimpulserhaltung zu retten. Dieses Teilchen wurde Neutrino genannt
und später direkt nachgewiesen.
c) Energie
Während die inneren Kräfte zum Drehimpils nicht beitragen, tragen sie zur Gesamtenergie eines Teilchensystems bei. Die Gesamtenergie erhält man durch Integration der Bewegungsgleichung über dri und Summation über alle Teilchen
m i a i = F i +Σ F ik
Die linke Seite ergibt wie im Kap. C.5
Σ m i ∫ a i • dr i = Σ 12 m i v 2i − Σ 12 m i v 20 = E kin − E kin0
Der erste Term auf der rechten Seite ergibt die Arbeit der äußeren Kräfte
Σ ∫ F i • dr i = W ext
der zweite die Arbeitsleistung der inneren Kräfte
Σ ∫ F ik • dr i + ∫ F ki • dr k = Σ ∫ F ik • dr ik = Wint
(rik = ri - rk)
Wenn die inneren oder äußeren Kräfte konservativ sind, kann man für sie ein Potential
definieren
-Wint = Epot int - Epot int 0
-Wext= Epot ext - Epot ext 0
Der Energiesatz hat dann die Form
Ekin + Epot ext + Epot int = E0
E0 ist die Gesamtenergie. Für eine sich zu einem Stern zusammenziehende Teilchenwolke
spielt die äußere potentielle Energie keine Rolle. Je kleiner die interne potentielle Energie bei
129
der Kontraktion wird, desto größer wird die kinetische Energie. Diese geht über in Rotationsenergie und kinetische Energie der ungeordneten Bewegung der Teilchen. Die mittlere kinetische Energie der ungeordneten Bewegung im Schwerpunktsystem Ekin(s) pro Teilchen ist proportional zur Temperatur T. Die Kontraktion des Sternes führt also im allgemeinen dazu, daß
sich der Stern aufheizt. Umgekehrt kühlt sich ein Gas, das man in einer Düse entspannt, ab,
weil die Translationsenergie zunimmt.
In der Physik der Gase spielt die äußere potentielle Energie häufig keine Rolle. Statt dessen
(s)
interessiert man sich dafür, wo die äußere Arbeit verbleibt. W ext = E kin + E potint ist im Grunde
genommen der erste Hauptsatz der Wärmelehre.
4. Stoßgesetze
a) Was ist ein Stoß?
Abb. 130: Was heißt schon Berührung?
Ein Stoß ist eine kurzzeitige Krafteinwirkung, bei der nicht der Verlauf im Einzelnen, sondern
nur das Resultat interessiert. Z.B. möchte man beim Stoß von zwei Kugeln aus der Anfangssituation die Bewegung nach dem Stoß vorhersagen. Bei einem Stoß brauchen sich zwei Körper
nicht zu berühren. Z.B. spricht man von einem Stoß, wenn zwei elektrisch geladene Teilchen
nahe aneinander vorbeifliegen. (Genaugenommen gibt es überhaupt keine Berührung zweier
Körper, wenn man die Kontaktstelle mit atomarer Auflösung betrachtet.) Charakteristisch für
einen Stoß ist, daß die Wechselwirkung nur in einem begrenzten Gebiet wirksam ist.
Stoßprozesse sind besonders in der Teilchenphysik von Bedeutung, da die meisten Informationen über Teilchen durch Stoßexperimente gewonnen wurden. Bei Stoßprozessen zwischen
atomen oder Elementarteilchen sind die Teilchen vor und nach dem Stoß nicht identisch, da
Umsetzungen stattgefunden haben. Bei einer Stoßionisation z.B. hat man nach dem Stoß mehr
Teilchen als vorher. Häufig nehmen Teilchen Energie auf z.B. bei Stoßanregung. Statt der Erhaltung der individuellen Teilchen gelten Erhaltungssätze für charakteristische Eigenschaften
der Teilchen wie Spin, Ladung, Leptonenzahl (= Zahl der Teilchen mit nur schwacher Wechselwirkung) u.s.w. Stöße behandelt man, indem man Erhaltungssätze, z.B. die Erhaltung der
130
Gesamtenergie und des Gesamtimpulses, auf die Situation vor und nach dem Stoß anwendet.
Ähnliche Methoden verwendet man bei Stoßwellen.
b) Grundbegriffe
Wir betrachten zwei Teilchen m1 und m2 mit den Geschwindigkeiten v1 und v2 vor dem Stoß
und u1 und u2 nach dem Stoß (s. Abb. 130). Die Erhaltungssätze sind dann
Energiesatz:
1 m v2 + 1 m v2 = 1 m u2 + 1 m v2 + Q
1 1
2 2
1 1
2 2
2
2
2
2
Impulssatz:
m1v1 + m2v2 = m1u1 + m2u2
Q ist die Wärmetönung des Prozesses. Bei Q = 0 ist der Stoß elastisch. Die Hauptaufgabe besteht darin, aus m1, m2, v1, v2 die 6 unbekannten Größen u1 und u2 auszurechnen. Vollständig
läßt sich dieses Problem lösen, wenn sich die Schwerpunkte der Teilchen auf einer Geraden
bewegen - man spricht dann vom zentralen Stoß - und wenn der Stoß elastisch verläuft. Das
Problem ist meistens in einem im Labor festen Koordinatensystem gestellt, läßt sich aber besonders einfach im Schwerpunktsystem der Teilchen behandeln, da hier die Impulse der
beiden
Abb. 131: Bei den Stoßgesetzen geht es um den Zusammenhang der Geschwindigkeiten vor und nach dem Stoß.
Teilchen untereinander, sowie vor und nach dem Stoß dem Betrage nach gleich sind. Die
möglichen Orte der Spitzen der Vektoren u1 und u2 liegen also auf einem Kreis.
c) Elastischer zentraler Stoß
α) Das Target ruht
Da es sich um einen zentralen Stoß handeln soll, gibt es nur eine Koordinate. Wir können z.B.
annehmen, es sei die x - Koordinate. Die Geschwindigkeiten können dann als Skalare geschrieben werden. Das ruhende Teilchen habe den Index 2 (v2 = 0). Energie - und Impulssatz
haben dann die Form
131
m1 v1 = m1u1 + m2 v2
m1v12 = m1u12 + m2v22
Die Gleichungen werden so umgeschrieben, daß die Daten des ersten Teilchens links stehen.
Die zweite Gleichung ergibt
m1(v12 - u12) = m2u22
m1(v1 - u1)(v1+ u1) = m2u22
Die erste Gleichung ergibt
m1(v1 - u1) = m2u2
Dividiert man nun beide Gleichungen, erhält man
v1 + u1 = u2
Man Eliminiert u2, indem man in die Impulsbilanz einsetzt.
m1v1 = m1u1 + m2v1 + m2u1
u 1 =v 1
m1 − m2
m1 + m2
(8)
m − m2 
m + m2 + m1 − m2
= v1 1
u 2 = v 1 + u 1 = v 1  1 + 1
m1 + m2 
m1 + m2
u 2 =v 1
2m 1
m1 + m2
(9)
Diskussion
Für m1 = m2 = m wird u1 = 0 und u2 = v1. Die Teilchen tauschen die Geschwindigkeiten
aus. Die Energie des ersten Teilchens wird vollständig auf das zweite Teilchen
übertragen.
Der
Schwerpunkt
bewegt
sich
im
Laborsystem
mit
v1/2.
Im
Schwerpunktsystem bewegt sich m2 mit v1/2 in entgegengesetzter Richtung. Nach dem
132
Zusammenstoß kehren beide Teilchen ihre Geschwindigkeiten um. Dadurch bewegt sich
im Laborsystem m1 mit u1 = v1/2 - v1/2 = 0 und m2 mit v1/2 + v1/2 = v1.
Für m2 << m1 wird u1 = v1 und u2
= 2v1. Das erste Teilchen behält seine
Geschwindigkeit bei, während das zweite Teilchen mit doppelter Geschwindigkeit des
ersten Teilchens den Stoßbereich verläßt. Da im zweiten Teilchen wegen der kleinen
Masse praktisch keine kinetische Energie steckt und sich m1 weiterhin mit v1 bewegt,
wird so gut wie keine Energie übertragen. Der Schwerpunkt des Systems ruht im
wesentlichen im schweren Teilchen. Im Schwerpunktsystem wird m2 an m1 reflektiert.
Wenn m2 >> m1 wird u1 = -v1. m1 wird reflektiert, währen m2 in Ruhe bleibt.
β) Die Energieübertragung
Mit den Formeln aus dem vorigen Abschnitt erhält man für die Energieübertragung q
q=
1
m u2
2 2 2
1
m v2
2 1 1
m
4 m 21
m 2 4v 21 m 21
=
=
(m 1 + m 2 ) 2 m 1 v 21 (1 + mm 21 ) 2
Zur Abkürzung wird das Massenverhältnis x genannt
q(x) =
4x
(1 + x) 2
Das Maximum dieser Funktion erhält man duch Nullsetzen der Ableitung
dq
(1 + x) 2 − 2x(1 + x)
(1 + x) − 2x
=4
= 4(1 + x)
4
dx
(1 + x)
(1 + x) 3
Abb. 132: Der Bruchteil der Energie, der auf den Stoßpartner übertragen wird, hängt vom Massenverhältnis ab.
Das Maximum liegt also bei x = 1, d.h. m1 = m2. Es gibt eine Reihe von Anwendungen. Z.B.
müssen in einem Kernreaktor die durch die Reaktion entstehenden Neutronen abgebremst
133
werden, da sonst die Wahrscheinlichkeit dafür, eine weitere Spaltung zu verursachen zu klein
wäre. Hierfür dient der Moderator. Als Moderator verwendet man bevorzugt wasserstoffhaltige Substanzen wie H2O (Leichtwasser), D2O (Schwerwasser), aber auch andere leichte Elemente, damit der Massenunterschied nicht zu groß ist. (H - Atome und Neutronen besitzen etwa die gleiche Masse).
Abb. 133: Viele Stoßprobleme gestalten sich besonders
einfach in einem Koordinatensystem, das im Schwerpunkt ruht.
γ) Beide Teilchen bewegen sich
Um aus den Gleichungen (8) und (9) die Formel für den Stoß auf ein Teilchen zu erhalten, das
sich bewegt, transformiert man sie auf ein Bezugssystem, das sich mit v0 bewegt. Die Geschwindigkeiten im bewegten System werden mit großen Buchstaben bezeichnet (s. Abb.
133). Für alle Geschwindigkeiten gilt v = V + v0.
0 = V 2 + v 0 → V2 = - v 0
v 1 = V 1 + v 0 = V 1 - V2
u1= U1 + v0 = U1 - V2
u 2 = U 2 + v 0 = U 2 - V2
Setzt man dies in die Gleichungen (8) und (9) ein, so erhält man
U 1 − V 2 = (V 1 − V 2 )
U1 =
m1 − m2
m +m
V 1 (m 1 − m 2 ) + V 2 (m 1 − m 2 ) + V 2 (m 1 + m 2 )
m +m
U1 =
V 1 (m 1 − m 2 ) + 2m 2 V 2
m1 + m2
Wegen der Symmetrie des Problems kann man die Indizes vertauschen.
134
U2 =
V 2 (m 2 − m 1 ) + 2m 1 V 1
m1 + m2
Abb. 134: Den Stoß zweier Kugeln, die nicht frontal
aufeinander stoßen kann man wie einen frontalen Stoß
behandeln, der senkrecht zur Tangentialebene verläuft.
d) Stoß mit seitlicher Impulsänderung
Treffen zwei Kugeln nicht frontal aufeinander, so wirkt doch die wesentliche Kraft senkrecht
auf die Berührungsfläche. Wenn man diese Richtung kennt, könnte man v1 und v2 in Komponenten parallel und senkrecht zu ihr zerlegen. In der Tangentialrichtung ergibt sich keine Impulsübertragung, in der senkrechten gilt das bisher gesagte. Häufig kennt man die Richtung
der Berührungsfläche nicht. Läßt man sie offen, kann man eine allgemeine Aussage über den
Ort der Spitzen von u1 und u2 machen. Es gilt der Energiesatz in der gleichen Form wie im vorigen Abschnitt und der Impulssatz für den vektoriellen Impuls. Wir betrachten den Fall v2 = 0
und interessieren uns für p2 = m2u 2 , dessen Komponenten wir deshalb x und y nennen. Nach
Abb. 135 erhält man
x2 + y2 = m22u22
(m1v1 - x)2 + y2 = m12 u12
Abb. 135: Das Dreieck der beteiligten Impulse. Das
Teilchen 2 ruht vor dem Stoß.
Der Energiesatz lautet
m1v12 = m1u12 + m2u22
Man eliminiert u12 und u22, v 1 wird als Parameter belassen.
m 1 v 21 = m1  (m 1 v 1 − x) 2 + y 2  + m1 (x 2 + y 2 ) = m 1 v 21 − 2v 1 x + m1 x 2 + m1 y 2 + m1 x 2 + m1 y 2
1
2
1
1
2
2
1 x2 + 1 y2
0 = −2v 1 x + µ
µ
x 2 + y 2 − 2µv 1 x = 0
135
Durch Hinzufügen der quadratischen Ergäzung auf beiden Seiten erhält man
(x − µv 1 ) + y 2 = (µv 1 )
2
2
Abb. 136: Der Impuls des anfangs ruhenden Teilchens kann unterschiedliche Richtungen annehmen. Die Spitzen aller möglichen Impulsvektoren liegen auf einem Kreis. Bei gleichen Massen ist dies der Thaleskreis und es
liegt ein rechter Winkel zwischen den Flugrichtungen nach dem Stoß.
Es ergibt sich ein Kreis mit dem Radius und der Verschiebung µv1 (Abb. 136).
m2
µv 1 =
m v ist der um das Massenverhältnis reduzierte Anfangsimpuls des Teilm +m 1 1
chens 1. Wenn m1 = m2, liegt der Mittelpunkt des Kreises auf der Mitte des Vektors m1v1. D.h.
die Spitzen der Vektoren m2u2 liegen auf dem Thaleskreis. Die Bewegungsrichtungen der
Teilchen bilden nach dem Stoß einen rechten Winkel.
e) Der inelastische Stoß
Abb. 137: Beim volständig inelastischen Stoß kleben
die Stoßpartner nach dem Stoß zusammen.
Wenn die Wärmetönung Q bekannt ist, können u1 und u2 wieder aus Impuls- und Energiebeziehung berechnet werden. Wenn Q nicht bekannt ist, aber beide Körper nach dem Stoß aneinander kleben, spricht man vom vollkommen unelastischen Stoß (Abb. 137). Dann gilt
u1 = u2 = u. u läßt sich alleine durch den Impulssatz bestimmen.
m1v1 + m2v2 = (m1 + m2)u
u=
m1v1 + m2v2
m +m
Beispiel: das ballistische Pendel
136
Abb. 138: Mit dem ballistischen Pendel läßt sich die
Anfangsgeschwindigkeit von Geschossen mit Hilfe der
Gesetze des inelastischen Stoßes bestimmen.
Zur Bestimmung der Geschwindigkeit eines Geschosses schießt man in einen als Pendel aufgehängten Behälter, in dem das Geschoß stecken bleibt. Aus der Auslenkung des Pendels ergibt sich sofort mgh und daraus die kinetische Energie unmittelbar nach dem Stoß.
1 m u 2 = m gh
2
2
2
Nach den Stoßgesetzen gilt (immer m2 >> m1 und v2 = 0 vorrausgesetzt)
m
u = m1 v1
2
Durch Eliminieren von u erhält man
2
1  m 1  v 2 = gh
2  m2  1
m 2
v 21 = 2gh  m 2 
1
137
KAPITEL E
Mechanik von Flüssigkeiten und Gasen
1. Vorbemerkungen über Gase, Flüssigkeiten und feste Körper
Gase, Flüssigkeiten und Festkörper sind Vielteilchensysteme. Die einzelnen Teilchen bewegen sich nach den Gesetzen der Mechanik im Kraftfeld der übrigen Teilchen und der Außenwelt. Die inneren Kräfte sind am größten im festen Körper, wo sie nur ein Schwingen der Atome um ihre Ruhelage zulassen, schwächer in der Flüssigkeit, wo eine Verschiebung der Atome gegeneinander möglich ist und die schnellsten Atome den Verband verlassen können. Im
Gas bewegen sich die Teilchen überwiegend frei zwischen kurzzeitigen Wechselwirkungen
beim Stoß mit anderen Teilchen oder der Wand. Durch die Vielzahl der Stöße wird eine Kraft
auf die Wand ausgeübt, die sich als Druck bemerkbar macht.
Flüssigkeiten und Gase zeigen gemeinsam keine Formstabilität, mit Ausnahme von Flüssigkeiten in kleinen Mengen, die zur Tropfenbildung neigen. Flüssigkeiten unterscheiden sich
von Gasen sehr stark in der Dichte. Die Dichte von Wasser, 1kg/l ist typisch für Flüssigkeiten,
die von Luft, 1,3g/l typisch für Gase. Gase sind im Gegensatz zu Flüssigkeiten stark komprimierbar. Eine ideale Flüssigkeit ist nicht komprimierbar und hat keine Scherkräfte, d,h, Kräfte, die bei der Verschiebung zweier Flüssigkeitsschichten gegeneinander auftreten, d.h. keine
Viskosität.
2. Druck in Gasen
Abb. 139: Auf einer genügend kleinen Fläche bemerkt
man die Stöße der einzelnen Teilchen.
Der Druck wird durch die Stöße der Teilchen mit der Wand verursacht. Die Kraftwirkung auf
eine genügend kleine Fläche der Wand besteht aus einer Folge von Kraftimpulsen. Der Mittelwert der Kraft wird durch Verschmierung über die Zeit t0 erhalten.
Ft 0 = ∫ F(t)dt
F = 1 ∫ F(t)dt
t0
138
Wir nehmen an, alle Teilchen haben eine Geschwindigkeit v auf die Wand zu. Die Teilchendichte n, d.h. die Anzahl der Teilchen pro Volumen, und ihre Masse sei bekannt. Der Druck
auf die Fläche soll berechnet werden. Die Größe ∫ F(t)dt nennt man Kraftstoß. Sie ergibt sich
aus Newtons Bewegungsgleichung.
•
P = F(t)
durch Integration. Der Impuls ist hier groß geschrieben, um ihn vom Druck p zu unterscheiden
∫ F(t)dt = P 2 − P 1 = 2mv
Stößt ein Teilchen mit dem Anfangsimpuls mv auf eine Wand, so kehrt der Impuls um wie bei
einem Stoß mit einer unendlich großen Masse. Die Impulsänderung ist also 2mv. Damit wird
F = 1 ∫ F(t)dt = 2mv
t0
2
für z Stöße
F = 2mv z = 2mvν
t
ν ist die Stoßfrequenz. Für einen Teilchenstrahl, der senkrecht zur Fläche gerichtet ist, braucht
man nur alle Teilchen abzählen, die in der Zeit t auf die Fläche treffen werden. Das sind in
Abb. 140 alle Teilchen, die sich in dem Volumen der Grundfläche A und der Höhe vt
befinden.
Abb. 140: Die Stoßzahl auf eine Wand läßt sich durch die
Dichte und Geschwindigkeit der Teilchen ausdrücken.
ν = N = nAvt = nAv
t
t
und
F = 2mnv 2 A
139
Der Druck ist definiert als p = F mit der Dimension [p] = N2 = Pa (Pascal). Der normale
A
Druck der Atmosphäre ist 1bar = 105 N/m2. Der Druck, den ein Teilchenstrahl ausübt, ist also
p = 2mnv2.
Bei isotroper Geschwindigkeitsverteilung fliegen sicher weniger Teilchen auf die Wand als
bei einem auf die Wand gerichteten Teilchenstrahl. Bei korrekter Vorgehensweise muß man
eine Mittelung über alle Geschwindigkeiten in Richtung und Größe vornehmen. Die Mittelung hat allerdings nur einen Einfluß auf einen Faktor vor dem Ausdruck für den Druck auf
die Wand. Die Abhängigkeit kommt korrekt heraus, wenn man statt der Mittelung von davon
ausgeht, daß alle Teilchen die gleiche Geschwindigkeit besitzen. Der Druck muß unabhängig
von der Form des Gefäßes sein. Wir dürfen daher annehmen, das Gas befände sich in einem
Würfel. Auf jede Fläche ströme 1/6 aller Teilchen. Die Zahl 6 rührt von den drei Dimensionen
mit ihren je zwei Richtungen her.
Abb. 141: Wegen der Isotropie der Geschwindigkeitsverteilung treffen auf jede Wand eines Würfels nur 1/6 aller
Teilchen.
Die Stoßzahl ist jetzt
ν = 1 nAv
6
und damit
p = 1 nmv 2
3
Man geht zurück auf die Gesamtzahl der Teilchen N = nV
pV = 1 Nmv 2
3
und definiert 1 mv 2 = 3 kT mit der Boltzmannkonstanten k = 1,38 10-23 J/K und erhält die allge2
2
meine Zustandsgleichung für ideale Gase
140
pV = NkT
Hieraus folgt, da individuelle Eigenschaften der einzelnen Gase nicht vorkommen, der Satz
von Avogadro:
Zwei verschiedene Gase mit gleichem p,V und T enthalten die gleiche Anzahl der Teilchen
In einem Gasgemisch muß für N die Gesamtzahl der Teilchen eingesetzt werden, dabei ist zu
beachten, daß man in einem ionisierten Gas die freien Elektronen als Teilchen mitzählen muß.
Die Menge des Gases, die die Avogadrozahl NA = 6·1023 Teilchen enthält, nennt man ein
Mol. 1 Mol wiegt in g soviel, wie das Atomgewicht ausmacht. Führt man die Anzahl der Mole
nm = N/NA ein, schreibt sich die Zustandsgleichung
pV = n m (kN A )T
Und nach einführen der Gaskonstante R = kNA = 8,3 J/K erhält man die übliche Form
pV = n m RT
(10)
Die Zustandsgleichung für ideale Gase enthält die Sonderfälle des Boyle - Mariotteschen Gesetzes pV = const für T = const und des Gay - Lussacschen Gesetzes p/T = const für V = const.
3. Hydrostatik
Die Hydrostatik befaßt sich mit den Druckverhältnissen in ruhenden Flüssigkeiten. Druck ist
in Flüssigkeiten und Gasen isotrop, d.h. unabhängig von der Ausrichtung der Fläche auf der er
ausgeübt wird.
a) Das Eigengewicht ist vernachlässigbar
Wenn das Eigengewicht keine Rolle spielt, ist ist der Druck sogar in der ganzen Flüssigkeit
konstant. Drückt man einen Kolben in ein Gefäß, sodaß keine Kompressionsarbeit im Medium
verrichtet wird, muß nach dem Energiesatz gelten
F1s1 = F2s2
und wegen der Konstanz des Volumens
141
Abb. 142: Die Tatsache, daß - bei Vernachlässigung des Eigengewichtes der Druck in einer Flüssigkeit überall gleich
ist, folgt aus dem Energiesatz
A1s1 = A2s2
Durch Division beider Gleichungen ergibt sich
F1 F2
also p1 = p2
=
A
A
Man nutzt die gleichmäßige Druckausbreitung in Flüssigkeiten in der Hydraulik zur Krafttransformation aus, z.B. in Hebebühnen, Bremsen, oder zur Kraftübertragung zur Bewegung
von Maschinenteilen wie Flugzeugrudern, Baggerarmen und dergleichen.
b) Druck aufgrund des Eigengewichts
α) Zylindrisches Gefäß
Abb. 143: In einem zylindrischen Gefäß ist der Druck am Boden die Gewichtskraft des Wassers geteilt durch die
Bodenfläche.
In einem zylindrischen Gefäß hat man am Boden den Druck
F G ρVg ρhAg
=
=
= ρhg
A
A
A
(11)
Dies ist der Satz von Stevin (Simon Stevin 1548 - 1620). Er bildet die Grundlage zum Messen
von Drucken mit flüssigkeitsgefüllten U - Rohren. Eine 10 m hohe Wassersäule macht einen
Druck von 10·103·9,81 Pa ≈ 1 bar. Sie kann daher vom Luftdruck im Gleichgewicht gehalten
werden. Größere Saughöhen von Wasserpumpen sind nicht möglich. Da die Dichte von
Quecksilber 13,5 mal so hoch ist, wie die von Wasser, entsprechen 740 mm Hg - Säule 1 bar.
142
1 mm Quecksilbersäule übt den Druck von 1 Torr aus. Die Einheit Torr ist nach dem italienischen Physiker Evangelista Torricelli (1608 - 1647) benannt.
β) Das hydrostatische Paradoxon
Abb. 144: In diesem Gefäß ist der Druck genau so groß wie
in einem zylindrischen mit gleicher Grundfläche und damit
kleiner als das Gewicht der Flüssigkeit geteilt durch die
Bodenfläche
Der Druck durch das Eigengewicht einer Flüssigkeit ist unabhängig von der Form des Gefäßes. In dem in Abb. 144 dargestellten Gefäß ist er z.B. kleiner als das Gesamtgewicht des
Wassers geteilt durch die Grundfläche. Den Grund für dieses Verhalten versteht man am besten, wenn man sich vorstellt, man führe in ein mit Flüssigkeit gefülltes Gefäß wie in Abb.145
eine Trennwand ein, so daß zunächst beide Teilvolumen verbunden bleiben. Durch das Einbringen dieser Wand ändern sich die Druckverhältnisse nicht. Versperrt man jetzt die Verbindung der beiden Teilvolumina, ändert sich noch immer nichts am Druck. Nimmt man jetzt die
Flüssigkeit aus dem oberen Teil des Gefäßes, ändert sich am Druck wieder nichts, weil keine
Verbindung zwischen den Teilvolumina bestand. Die kleinere Wassermenge erzeugt den
gleichen Druck wie die ursprüngliche größere. Die fehlenden Kräfte werden durch Reaktionskräfte der Zwischenwand erzeugt.
Abb. 145: In dem durch die gestrichelten Flächen abgeteilten Teilvolumen ist der Druck genau so groß wie in dem gesamten Volumen.
c) Der Auftrieb
α) Satz von Archimedes
Ein in eine Flüssigkeit eingetauchter Körper erfährt aufgrund des Satzes von Stevin auf seiner
Unterseite eine größere Kraft als auf seiner Oberseite. Die Resultierende ist die Auftriebskraft.
Bei einem Quader der Grundfläche A und der Höhe h ist die Kraft auf die Grundfläche
FU = ρFlg(H+h)A, auf die Deckfläche FO = ρFlgHA. Die Gesamtkraft FA = FO - FU = ρFlghA ist
143
Abb. 146: Durch den Druckunterschied zwischen der oberen
und unteren Begrenzungsfläche des Würfels entsteht ein
Auftrieb.
gleich dem Gewicht der verdrängten Flüssigkeit. Einen Körper beliebiger Form denkt man
sich aus derartigen Quadern zusammengesetzt. Man erhält den Satz von Archimedes:
Der Auftrieb ist gleich dem Gewicht der verdrängten Flüssigkeitsmenge
Nach Stevin beweist man den Satz wie folgt: Man ersetzt einen Körper beliebiger Form durch
einen Flüssigkeitskörper der gleichen Form. Dieser wird in Ruhe bleiben, da jetzt ja eine homogene Flüssigkeit vorliegt, für die es keinen Anlaß gibt, sich zu bewegen. Er erfährt also einen Auftrieb, der gleich seinem Gewicht ist. Da bei dem ursprünglichen Körper alle äußeren
Verhältnisse die gleichen sind, ist auch der Auftrieb gleich. Im folgenden werden einige Anwendungen des Satzes von Archimedes gezeigt.
β) Schiffshebewerke
Da bei schwimmenden Körpern die verdrängte Flüssigkeit soviel wiegt wie der gesamte Körper, wird ein Wasserbecken, in das ein Schiff fährt, dadurch nicht schwerer. Man kann also
zum Heben von Schiffen in solchen Becken das Gewicht durch ein Gegengewicht ausgleichen
und muß nur noch die Reibungskräfte überwinden.
γ) Bestimmung der Dichte eines Körpers
Man wägt einen Körper in Luft, erhält das Gewicht FL = mKg, taucht ihn in Wasser und erhält
das Gewicht FW = mKg - VKρWg. Der zweite Term berücksichtigt den Auftrieb. VK ist das Volumen des Körpers, ρW die Dichte des Wassers. Durch Division beider Gleichungen erhält
man
ρW
VKρW
FW
=1− m =1− ρ
K
K
FL
ρK =
1 ρ
W
F
1 − FW
Da nur das Verhältnis der Gewichte eingeht, kann man die Wägung mit einer ungeeichten Feder durchführen. Mit dieser Methode konnte Archimedes angeblich die Echtheit einer goldenen Krone überprüfen. Gold hat eine deutlich höhere Dichte als die Metalle, mit denen man es
144
fälschen kann. Die Methode ist auch geeignet, um bei bekannter Dichte eines Körpers die einer Flüssigkeit zu bestimmen.
δ) Das Aräometer
Abb. 147: Im Aräometer wird der Auftrieb zu Bestimmung der Dichte einer Flüssigkeit ausgenutzt.
Das Aräometer ist ein Schwimmkörper zur Bestimmung der Dichte einer Flüssigkeit, z.B. zur
Messung von Konzentrationen. Jeder schwimmende Körper sinkt so tief ein, bis die verdrängte Flüssigkeit genau so viel wiegt, wie der gesamte Körper. Wenn die Flüssigkeit spezifisch
schwerer ist, wird deshalb der Körper weniger tief einsinken als wenn sie leichter ist. Um eine
möglichst empfindliche Anzeige zu machen, wird der Körper wie in Abb. 147 geformt. Dadurch verdrängt er im Bereich der Anzeige nur wenig mehr, wenn er eine größere Höhe
eintaucht.
d) Die Barometrische Höhenformel
Da Luft komprimierbar ist, ändert sich mit dem Druck die Dichte
= ρ kT
p = NkT = Nm kT
m
V
V m
(12)
m ist die Masse eines Moleküls. Dadurch ist der Satz von Stevin, der für konstante Dichte abgeleitet wurde, nicht mehr gültig. Um den Druck in Abhängigkeit von der Höhe p(h) zu berechnen, teilt man die Luftsäule in Schichten der Höhe ∆h, die so klein sind, daß sich innerhalb p nicht ändert. Dann gilt
∆p = −ρg∆h
Abb. 148: In der Athmosphäre gilt der Satz von Stevin wegen der
Kompressibilität der Luft nur für kleine Höhenunterschiede.
145
(Der Druck nimmt mit steigender Höhe ab). dp wird über Gleichung (12) durch dρ ersetzt.
dp = kT
m dρ
also
kT dρ = −ρgdh
m
ρ wird auf die linke Seite geschafft
dρ
mg
=
−
dh
ρ
kT
Integration rechts und links:
∫ρ
ρ
0
ρ
dρ
ρ
ρ = [ln ρ] ρ 0 = ln ρ 0,
ln ρ/ρ 0 = −
ergibt
∫
h
dh = h
mgh
kT
rechts und links wird der Exponent gebildet, und dabei ausgenutzt, daß elnx = x.
ρ
mgh/kT
= e −E pot /kT
ρ0 = e
(13)
Wegen Gleichung (12) ist das Verhältnis der Dichten gleich dem der Drucke. Schreibt man
außerdem den Exponenten in dimensionsloser Form, erhält man
p
−h/h 0
p0 = e
mit h0 = 8000m. Dichte und Druck fallen bei konstanter Temperatur exponentiell ab (Abb.
149). Da die Temperatur in K gemessen wird, ist die Annahme konstanter Temperatur nicht
allzu kühn. Bei h = h0 hat der Druck auf 1/e abgenommen.
Abb. 149: Die Abnahme der Dichte der Luft mit der Höhe
nach der barometrischen Höhenformel.
146
e) Die Oberflächenspannung
α) Was ist Oberflächenspannung?
Kräfte zwischen den Molekülen der Flüssigkeit (Kohäsionskräfte) und zwischen der Flüssigkeit und einer Wand (Adhäsionskräfte) modifizieren das Verhalten der Flüssigkeit über kleine
Distanzen, z.B. in Tropfen und in wandnahen Zonen. Diese Phänomene beschreibt man durch
Oberflächenspannung. Im Innern einer Flüssigkeit heben sich alle Kohäsionskräfte auf. An der
Oberfläche sind nur ein Teil der Kohäsionskräfte vorhanden (s. Abb.150).
Abb. 150: Auf Teilchen an der Oberfläche wirkt eine andere
Gesamtkraft durch die Nachbarteilchen als auf Teilchen im
Innern.
Ein Teilchen hat durch diese Kräfte an der Oberfläche eine höhere Energie als im Zentrum.
Die Kräfte besitzen eine Reichweite von etwa 10-7cm. Da die Flüssigkeit bestrebt ist, den Zustand kleinster Gesamtenergie einzunehmen, hält sie die Oberfläche möglichst klein. Dieses
Bestreben, die Oberfläche zusammen zu ziehen, erscheint wie eine Kraft, die tangential zur
Oberfläche wirkt und die zusätzlich zur Gravitation auftritt.
Beim Vergrößern der Oberfläche um ∆A muß eine Energie ∆E aufgebracht werden, die proportional zur Oberfläche ist.
∆E = σ∆A
(14)
σ ist die Oberflächenspannung. Sie hat nach ihrer Definition in Gleichung (13) die Dimension
[σ] = Nm2 = Nm −1
σ = 0,008N/m für Wasser. σ ist stark von der Verunreinigung abhängig. Zieht man mit einem
Drahtbügel eine Flüssigkeitslamelle aus einer Oberfläche, so ist
Fs = ∆E = σ∆A = 2σls
147
Abb. 151: Zur Messung der Oberflächenspannung wird
mit einem Drahtbügel eine Lamelle aus der Flüssigkeit gezogen. Die Lamelle hat eine Oberfläche 2l·s (rechts).
σ = F/2l
Der Faktor 2 rührt daher, daß eine Flüssigkeitslamelle zwei Oberflächen besitzt (s. Abb. 151),
und daher ihre Gesamtoberfläche 2sl ist. Die Kraft ist nicht von der Fläche sondern nur von
der Länge, über die F angreift, abhängig. Die Oberflächenspannung kann man zur Beeinflussung der Benetzung einer Fläche und zur Herstellung von Minimalflächen anwenden. Ihre
Messung dient z.B. zur Bestimmung der Reinheit einer Flüssigkeit.
β) Die Seifenblase
Abb. 153: Die Arbeit, eine Seifenblase um ∆r aufzublasen.
Um den Druck in einer Flüssigkeitskugel aufgrund der Oberflächenspannung auszurechnen,
betrachten wir die Arbeit ∆E, die der innere Druck p bei einer Vergrößerung des Radius um
∆r leistet.
∆E p = F∆r = pA∆r = p4πr 2 ∆r
Dies entspricht einer Vergrößerung der Oberflächenenergie
∆E O = σ∆A
Da A = 4πr2 folgt durch Differentiation dA = 8πr und damit ∆EO = σ8πr∆r. Die hineingedr
steckte Arbeit wird in Energie der Oberfläche gewandelt. Also gilt ∆Ep = ∆EO und damit
148
p4πr2∆r = σ8πr∆r
p = 2σ
r
Wegen der äußeren und inneren Oberfläche der Haut einer Seifenblase gilt für diese
p = 4σ
r
Der Druck in einer kleinen Seifenblase ist größer als in einer großen.
γ) Die Haftspannung
Abb. 153: Die Wölbung der Oberfläche am Rand hängt mit
den Oberflächenspannungen an den verschiedenen Grenzflächen zusammen.
Wenn wir bisher von Oberflächenspannung gesprochen haben, haben wir an die Grenzfläche
zwischen Flüssigkeit und Luft gedacht. Natürlich gibt es auch eine Oberflächenspannung an
der Grenzfläche zwischen Flüssigkeit und einer Wand. Der Koeffizient der Oberflächenspannung hängt von dem angrenzenden Medium ab. Im Randbereich von Flüssigkeiten in Gefäßen
sind daher drei verschiedene Oberflächen mit den Kräften Fik = σikl maßgeblich (s. Abb. 153).
Die Neigung der Oberfläche stellt sich so ein, daß - wenn möglich - sich diese drei Kräfte im
Gleichgewicht befinden. Da alle drei Kräfte an der gleichen Randlänge l angreifen, kann man
bei der Aufstellung der Kräftebilanz statt der Kräfte die ihnen proportionalen Oberflächenspannungen σik verwenden. σH = σ23 - σ13 ist die Haftspannung (s. Abb. 154). Wenn σH > 0, ist
die Flüssigkeit nicht benetzend wie in Abb. 154. Die Neigung der Oberfläche stellt sich so ein,
daß sich die Komponenten der Kräfte in Wandrichtung kompensieren
σ12cosθ = σH
149
Abb.
154:
Benetzende
und
nicht
benetzende
Flüssigkeiten.
Für σH < 0 ist die Flüssigkeit benetzend. cosθ ist dann kleiner 0 und der Winkel θ wird
stumpf. Für |σH | > σ12 nennt man die Flüssigkeit vollständig benetzend. Sie kriecht an der
Wand hoch.
δ) Kapillarität
In Röhrchen, die in eine Flüssigkeitsoberfläche getaucht werden und die dünner sind als die
Ausdehnung der Randzone, steigen benetzende Flüssigkeiten auf (Abb. 155), nicht benetzende
werden nach unten gedrückt. Die Flüssigkeitsoberfläche nimmt Kugelgestalt an, da dies eine
Minimalfläche bei festem Volumen ist. Man kann also die Formel für den Innendruck von Kugeln verwenden und diesen dem hydrostatischen Druck gleichsetzen.
ρgh = 2σ
R
Diese Formel erlaubt es, aus der gemessenen Steighöhe auf die Oberflächenspannung zu
schließen, wenn man den Krümmungsradius der Oberfläche ermittelt. Manchmal wird statt
dessen auch der Haftwinkel θ gemessen. Dieser hängt mit R zusammen (s. Abb. 155) über
cosθ = r/R.
Abb. 155: Bei genügend dünnen Kapillaren ist die
Oberfläche kugelförmig, und man kann mit dem
Druck von Kugelflächen rechnen.
150
Abb. 156: Die Stromlinie ist eine Kurve, die überall tangential zur Geschwindigkeit verläuft.
4. Hydrodynamik
a) Das Geschwindigkeitsfeld
α) Grundbegriffe
Die Strömung einer Flüssigkeit beschreibt man durch das Geschwindigkeitsfeld v(x,t). Die
Kurven, die in jedem Punkt tangential zu v verlaufen, nennt man die Stromlinien. Durch jeden
Punkt läuft eine Stromlinie. In diesem Sinne ist die Anzahl der Stromlinien unendlich. Ist v
nicht explizit von der Zeit abhängig, nennt man das Geschwindigkeitsfeld stationär und die
Stromlinie ist mit der Bahn eines Teilchens identisch. Die Zeitableitung der Geschwindigkeit
∂v
an einem Ort schreibt man
, die für ein Flüssigkeitsteilchen dv . Die letztere nennt man
∂t
dt
auch die substantielle Ableitung. In einer stationären Strömung ist also ∂v = 0 . Eine Flußröhre
∂t
ist eine Röhre, deren Wand parallel zu den Stromlinien liegt.
β) Der Fluß Φ
Das Volumen, das pro Sekunde durch die Fläche A tritt, nennt man den Fluß durch diese Fläche. Nach dem in Kapitel C.2.c gesagten errechnet sich der Fluß aus
Φ = ∫ v • dA
Für eine Strömung, bei der die Geschwindigkeit über den Querschnitt konstant ist, vereinfacht
sich dies zu
Φ = v • A = vAcosα = v ⊥ A
Abb. 157: Der Fluß durch die Kontrollflächen 1 und 2 ist im
stationären Zustand gleich.
151
wobei v⊥ die Geschwindigkeitskomponente senkrecht zur Fläche A ist. Der Fluß, der durch eine bestimmte Kontrollfläche einer Flußröhre fließt, ist unabhängig von der genauen Form der
Kontrollfläche.
γ) Die Kontinuitätsgleichung
Hat man keine Quellen (b.z.w. Teilchenverluste) in einer stationären Strömung, gilt Massenerhaltung, d.h. die gesamte Masse, die pro Sekunde durch eine Fläche strömt, ρΦ = ρv⊥A ist an
jeder Stelle der Flußröhre die gleiche.
ρv ⊥ A = const
entlang der Flußröhre
In einer inkompressiblen Flüssigkeit ist ρ = const und daher
Av ⊥ = const
entlang der
Fluß- röhre. d.h. bei Querschnittsverengungen muß die Geschwindigkeit entsprechend erhöht
sein. Dieser Effekt ist aus dem täglichen Leben bei Menschenströmen durch einen schmalen
Durchlaß bekannt.
δ) Anzahl der Stromlinien
Zur graphischen Veranschaulichung eines Strömungsfeldes zeichnet man eine beliebige aber
endliche Zahl von Stromlinien. Da in einer inkompressiblen stationären Strömung die Zahl der
Stromlinien in einer Flußröhre konstant ist, und ebenso der Fluß Φ konstant ist, ist Φ proportional zur Anzahl der Stromlinien N: Φ ~ N. Die Ausdrucksweise "Zahl der Stromlinien" bekommt dadurch einen quantitativen Sinn. Wenn wir "Zahl der Stromlinien" sagen, meinen wir
den Fluß oder eine zum Fluß proportionale Größe. Da außerdem Φ = v⊥A, ist v⊥ ~ Φ/A. Die
Geschwindigkeit läßt sich aus der Stromliniendichte ablesen. z.B. muß in einer Windströmung
über ein Hausdach die Geschwindigkeit des Windes im Firstbereich größer sein als in der ungestörten Strömung. Bei Geschwindigkeiten, die sehr viel kleiner als die Schallgeschwindigkeit sind, kann die Kompressibilität der Luft im allgemeinen vernachlässigt werden.
Abb. 158: Über dem Hausdach ist die Windgeschwindigkeit größer als in der ungestörten Strömung.
152
b) Die Bewegungsgleichung
α) Die Eulerschen Gleichungen
Abb. 159: Kräfte auf ein Volumenelement.
In einer Stromröhre mit veränderlichem Querschnitt soll sich Flüssigkeit unter dem Einfluß
des Druckes in x - Richtung bewegen. Die Kräfte auf ein Flüssigkeitsvolumen der Größe
dV = dAdx (s. Abb. 159) werden betrachtet, wobei äußere Kräfte Fext (z.B. Gravitation) und
Druckkräfte Fp = pdA unterschieden werden. Kräfte, Masse, und potentielle Energie werden
auf ein Einheitsvolumen bezogen.
f = dF ,
dV
ρ = dm
dV
Dann gilt für die Kraft auf das Volumen in eine Richtung x, da die Gesamtkraft die Differenz
der Kräfte auf die Stirnflächen ist,
dFp = pdA - (p + dp)dA = -dAdp= -dA(dp/dx)dx
dF p = −
fp = −
dp
dV
dx
dp
dx
Die Gravitationskräfte pro Volumen schreiben sich
fG =
dF G dmg
=
= ρg
dV
dV
Dividiert man die Newtonsche Bewegungsgleichung durch das Volumen, erhält man
•
ρv =−
dp
+ ρg
dx
153
Im dreidimensionalen Raum gilt für jede Koordinate eine solche Gleichung
•
∂p
•
∂p
•
∂p
ρ v x = − dx + f ext,x
ρ v y = − ∂y + f ext,y
ρ v z = − ∂z + f ext,z


Indem man den Vektor 


schreiben
∂p
∂x
∂p
∂y
∂p
∂z


 = gradp einführt, kann man die Bewegungsgleichung vektoriell


•
ρ v = − gradp + f ext
(15)
gradp ist ein Vektor, der die Größe und Richtung der Druckkräfte anzeigt. Gleichung (15)
•
nennt man die Eulerschen Gleichungen für die Bewegung veiner nichtviskosen Flüssigkeit.
ist die substantielle Ableitung dv . Wenn die Bahn eines Massenteilchens x(t) ist und die Strödt
mung eindimensional und stationär verläuft, wird
dv(x) dv dx
=
= v dv
dt
dx dt
dx
Obgleich alle Zeitableitungen verschwinden (es wurde eine stationäre Strömung vorausgesetzt), ergibt sich eine Geschwindigkeitsänderung. Diese entsteht dadurch, daß sich Teilchen
im Verlaufe ihrer Bewegung in Gebieten unterschiedlicher Geschwindigkeit aufhalten. Vektoriell ergibt sich dieser "konvektive Term" zu (v•∇)v.
c) Der Satz von Bernoulli
α) Herleitung
Durch Integration der Bewegungsgleichung über den Ort erhält man den Energiesatz, durch
Integration der Eulerschen Gleichungen den Satz von Bernoulli. Für eine eindimensionale
Strömung (z.B. entlang einer Flußröhre) gilt
154
Abb. 160: Eine Flußröhre ist von Stromlinien ummantelt
d  1 ρv 2  = ρv dv = ρv dv dt = ρ v• (oder vektoriell grad  1 ρv 2  = ρ v• )

2

ds  2
ds
dt ds
Wenn die äußeren Kräfte ein Potential haben, ist
F ext = − d E pot
ds
f ext = − d e pot
ds
(oder vektoriell Fext = -grad Epot)
wobei e pot =
Die Druckkräfte haben die Form f p = −
dp
ds
dE pot
dV
(oder vektoriell f p = −gradp)
Damit lautet die Eulergleichung
d  1 ρv 2  + d p + d e = 0
pot
 ds
ds  2
ds
Integriert man über die Koordinate entlang der Flußröhre s, erhält man die Bernoulli Gleichung (Daniel Bernoulli, 1700 - 1782)
1 ρv 2 + p + e = const
pot
2
(16)
In dieser Gleichung ist der Sonderfall der Hydrostatik enthalten. Indem v = 0 gesetzt wird, ergibt sich der Satz von Stevin einschließlich der gleichmäßigen Ausbreitung der von außen aufgeprägten Drucke. Das früher schon mal behandelte Ausströmen aus einem Loch am Boden
eines Gefäßes erhält man, indem man an den beiden Stellen 1 und 2 (Abb. 161) den Umgebungsdruck p1 = p2 = p einsetzt, und das ganze Gefäß als Stromlinie ansieht. Mit v1 = 0, v2 = v,
ρgh1= 0, ρgh2 = ρgh wird Bernoullis Satz dann 1 ρv 2 + p = ρgh + p und
2
v = 2gh
155
Abb. 161: Die maximale Ausströmgeschwindigkeit ergibt
sich aus dem Satz von Bernoulli.
Abb. 162: Druckverhältnisse in einer Düse
Was wir schon kennen. Für Strömungen, in denen die Potentialunterschiede keine Rolle spielen, setzen wir in der Bernoulli Gleichung epot,1 = epot,2 und erhalten
1 ρv 2 + p = 1 ρv 2 + p
1
2
2 1
2 2
Mit dieser Gleichung ergibt sich in einer Verengung in einer Düse wie in Abb. 163 der geringste Druck in der Strömung. Diese Tatsache erscheint zunächst paradox, da man meint, hier
müßte sich das strömende Medium zusammendrücken und damit auch einen höheren inneren
Druck verursachen. Man nennt dieses Ergebnis daher manchmal auch das hydrodynamische
Paradoxon. Der Demonstrationsversuch zeigt, daß in der Tat in der stärksten Verengung der
Druck am kleinsten ist. Der Physikalische Grund liegt darin, daß in der Düse aufgrund der
Kontinuitätsgleichung die größte Geschwindigkeit vorliegen muß. Diese Erhöhung der Geschwindigkeit bei Hineinfließen in die Verengung muß durch Druckkräfte erzeugt werden.
Das ist nur möglich, wenn der Druck an der Stelle höherer Geschwindigkeit kleiner wird.
β) Anwendungen
Abb. 163: Die Venturidüse
Die Druckerniedrigung in Verengungen wird in der Venturidüse zum Messen von Geschwindigkeiten ausgenutzt. In der Wasserstrahlpumpe (oder anderen Treibmittelpumpen) benutzt
man den Unterdruck zum Pumpen, im Bunsenbrenner zum Ansaugen von Luft. Tragflächen
156
Abb. 164: Die Wasserstrahlpumpe
Abb. 165: Die Wirkung des Tragflächenprofils
haben ein Profil, das die Luft zum überwiegenden Teil über die Oberseite lenkt. Dadurch wird
oben der Druck kleiner als unten, was zu einem Auftrieb führt: Fauf = (pu - po)A. Aus dem gleichen Grund werden Hausdächer durch den Wind nicht nach unten gedrückt, sondern nach
oben gehoben.
Abb. 166: Oben: Anordnung zur Messung des statischen Druckes.
Mitte: Messung des Gesamtdruckes
Unten: :Messung des Staudruckes mit dem Prandtlschen Staurohr.
Den statischen Druck p in der Bernoulligleichung mißt man mit einem mit der Strömung
schwimmenden Manometer. Da die Teilchen keine gerichtete Geschwindigkeit senkrecht zu
den Stromlinien haben, kann man auch ein feststehendes Manometer benutzen, dessen Eintrittsöffnung parallel zu einer Stromlinie ausgerichtet ist. Richtet man die Eintrittsfläche senkrecht zur Stromlinie aus, so wird unmittelbar vor der Öffnung v = 0. Die Strömung ist hier also stark gestört. Für eine Stromröhre, die das Gebiet mit v = 0 durchsetzt, heißt dies, daß aufgrund der Bernoulli Gleichung p0 = ½ρv2 + p = 0 + p1 entlang der Stromlinie konstant ist. Der
gemessene Druck ist gleich dem Gesamtdruck p0 der ungestörten Strömung. Das Prandtlsche
Staurohr (Abb. 166 unten) mißt die Differenz p0 - p = ½ρv2 und kann daher zur Geschwindigkeitsmessung verwendet werden.
157
d) Innere Reibung von Flüssigkeiten
α) Was ist Viskosität?
Bei einer laminaren Strömung üben benachbarte Schichten, die eine unterschiedliche Geschwindigkeit haben, eine Kraft in Strömungsrichtung aus. Wegen der innigen Berührung dieser
Schichten
ist
die
Reibungskraft
im
Unterschied
zu
der
Situation
bei
Festkörperobereflächen
Abb.167: Die Viskosität rührt von Reibung zwischen benachbarten Flüssigkeitsschichten unterschiedlicher Geschwindigkeit her.
zur Fläche der Schicht proportional. Nach Newton ist sie außerdem der Änderung der Geschwindigkeit senkrecht zur Strömungsrichtung proportional
F x = ηA
dv x
dy
η ist die Viskosität mit der Einheit [η] = Ns/m2 = Pas = kgm-1s-1 = 10 poise. Neben dieser sogenannten dynamischen Zähigkeit benutzt man auch die kinematische Zähigkeit ν = η/ρ oder
die Fluidität σ = 1/η.
Für ein Gas läßt sich die Viskosität aus einer mikroskopischen Beschreibung, der kinetischen
Theorie, ermitteln. Die Anzahl der zwischen zwei benachbarten Gasschichten überwechselnden Teilchen ist nvthA, wenn vth die mittlere thermische Geschwindigkeit der Teilchen ist. Außerdem muß für die Größe des Impulses, den ein Teilchen mitbringt, m∆v, der Geschwindigkeitsunterschied zu der Schicht betrachtet werden, aus der der Impuls kommt, d.h., die die
freie Weglänge λ von der betrachteten Schicht entfernt liegt. Entwickelt man die Strömungsgeschwindigkeit bezüglich der Koordinate x senkrecht zur Strömung und setzt für dx die freie
Weglänge d.h. die Strecke, die ein Teilchen fliegt, ohne gestoßen zu haben ein, so erhält man
∆v = dv λ
dx
Die Kraft auf eine Schicht der Strömung ist dem Impulsübertrag auf diese Schicht pro Zeit
proportional
158
F ∼ nv th A ⋅ m∆v = nmv th λA dv
dx
Man erkennt, daß sich der Newtonsche Ansatz reproduzieren läßt und daß
Tab. 1: Die Viskosität von Wasser in Abhängigkeit von der Temperatur
η ∼ nmv th λ
Man beachte, daß die Viskosität um so größer wird, je seltener Stöße zwischen Teilchen stattfinden. Außerdem nimmt bei Gasen η mit der Temperatur zu (T ~ vth2). Bei Flüssigkeiten
nimmt η mit steigender Temperatur ab, wie von Schmierölen bekannt ist. Die Temperaturabhängigkeit der Viskosität von Wasser ist in Tabelle I dargestellt.
Empirisch läßt sich das Verhalten recht gut mit η(t) = aeb/T beschreiben. Um dies zu verstehen,
stellt man sich die Flüssigkeitsschten als feste Schichten mit gewellter Oberfläche vor, die aneinander vorbei gleiten. Die thermische Bewegung entspricht einer Schüttelbewegung der
Schichten. Hierdurch bleibt die Berührung auf die Erhebungen der gewellten Oberflächen beschränkt. Vornehmer ausgedrückt, müssen die Teilchen zum Platzwechsel einen Potentialwall
überwinden. Aufgrund der Boltzmannverteilung nn ∼ e −∆E/kT geht dies bei höheren Tempera0
turen leichter.
β) Die Grenzschicht
Strömt Flüssigkeit laminar über eine Wand, so bleibt die wandnächste Schicht an dieser haften. In einem Bereich in der Nähe der Wand ändert sich die Geschwindigkeit, außerhalb liegt
die ungestörte Strömung vor. Der Bereich, in dem sich v ändert, heißt die laminare Grenzschicht. In ihr treten viskose Kräfte auf. Die Dicke läßt sich durch folgenden Gedanken abschätzen: Wenn man eine feste Fläche parallel zu seiner Oberfläche um eine Distanz l durch
die zähe Flüssigkeit zieht, leistet man die Arbeit
159
Abb. 168: Zur Definition der Schichtdicke
W R = F R l = ηA dv l
dy
Geht man von einer linearen Geschwindigkeitsänderung aus und nennt die Halbwertsbreite
v
des Geschwindigkeitsprofils die Schichtdicke D, so ist dv = 0 und die Reibungsarbeit
dy 2D
W R = ηA
v0
l
2D
Nimmt man an, daß sich die geleistete Arbeit ganz in der kinetischen Energie der beschleunigten Flüssigkeit wiederfindet, so ist
Av
E kin = 1 mv 20 = 1 ρADv 20 = η 0 l
2
2
2D
Dies ist eine Bestimmungsgleichung für die Schichtdicke.
D=
ηl
v0ρ
(17)
Bei kleiner Viskosität ist die Schichtdicke klein, daher ist dv/dx groß, so daß die Reibungskräfte trotzdem groß sein können.
γ) Die stationäre Rohrströmung
i. Das Geschwindigkeitsprofil
Nach dem Ansatz von Newton sind die Reibungskräfte auf eine zylindrische Flüssigkeitsschicht vom Radius r (Abb. 169)
Abb. 169: Die Flächen konstanter Geschwindigkeit sind bei
der Rohrströmung Zylinderflächen.
160
F z = η2πrl dv
dr
Die Kraft wird durch den Druck auf die Zylinderfläche mit dem Radius r aufgebracht
Fz = Apπr2
Daher gilt
dv = ∆p r
dr 2lη
Das positive Vorzeichen rührt daher, daß die Flüssigkeit bei in positiver x - Richtung abnehmenden Druck, eine in radialer Richtung abnehmende Geschwindigkeit erhält. Durch Integration ergibt sich
v(r) =
∆p 2
r +C
4lη
Die Integrationskonstante C bestimmt sich aus der Bedingung v(R) = 0.
C=−
und damit
∆p 2
R
4lη
v(r) =
∆p 2
∆p 2 2
(r − R 2 ) = −
(R − r )
4lη
4ηl
Da r < R ergibt sich bei in positiver x - Richtung abnehmendem Druck eine Geschwindigkeit
in x - Richtung. Die Geschwindigkeit besitzt in Abhängigkeit von der radialen Position ein
Parabelprofil (Abb. 170). Die äußere Kraft ∆pπR2 kompensiert die Reibungskräfte. Sie ist proportional zu v(0).
Abb. 170: Das Geschwindigkeitsprofil ist parabelförmig.
ii. Die Durchflußmenge
161
Die Durchflußmenge (der Volumenstrom) durch einen schmalen Ring der Fläche
dA = 2πrdr
ist
∆p
Φ = dV =vdA =
π(R 2 r − r 3 )dr
dt
2ηl
Abb. 171: Das Flächenelement, über das hier integriert
wird, ist ein Ring der Breite dr.
Durch Integration erhält man das Hagen - Poiseuillesche Gesetz.
dV = ∆p π  R 2 R 2 − R 4 
4 
8ηl  2
dt
dV = ∆p πR 4
dt
8ηl
(18)
8ηl
ist der Ströπ 4
mungswiderstand. Das Gesetz kann zur Bestimmung von η benutzt werden. Der Widerstand
Das Hagen - Poiseuille Gesetz ist das Ohmsche Gesetz für Strömungen.
wächst bei kleiner werdendem Radius mit R4.. Dies hat katastrophale Auswirkungen bei der
Arterienverkalkung im Alter.
δ) Das Stokessche Gesetz
Abb. 172: Stromlinienbild einer umströmten Kugel.
Bei der laminaren Umströmung einer Kugel rührt der Widerstand ebenfalls von der Reibung
zwischen benachbarten Flüssigkeitsschichten her und nicht von einer direkten Impulsübertragung auf die Stirnflächen der Kugel. Ohne Reibung wären die Druckkräfte aufgrund des Satzes von Bernoulli bei symmetrischem Stromlinienbild symmetrisch. Die Teilchen gewinnen
durch ein Druckgefälle von A nach B (Abb. 172) kinetische Energie, die es ihnen erlaubt,
162
gegen das Druckgefälle von B nach C anzulaufen. Die resultierende Kraft ist Null. Mit Reibung ergibt sich nach Stokes
F = 6πηrv
ε) Die Reynoldszahl
Physikalische Probleme, die theoretisch nur unzureichend zu beschreiben sind, behandelt man
häufig, indem man Unteresuchungen an Modellen macht und die Ergebnisse auf das ursprüngliche Problem überträgt. Dabei wird vorausgesetzt, daß sich das Modell und das ursprüngliche
System ähnlich verhalten. Der Zusammenhang zwischen analogen Größen im Modell und im
Original wird durch Skalierungsgesetze beschrieben.
Abb. 173: Geometrisch ähnliche
Figuren.
Für geometrische Ähnlichkeit fordert man, daß das Verhältnis analoger Längen gleich bleibt.
In dem Boot von Abb. 173 z.B.
l1 h1
=
l2 h2
Bei Ähnlichkeit bezüglich eines physikalischen Problems muß das Verhältnis anderer relevanter physikalischer Größen konstant bleiben. Ein solches Verhältnis ist eine dimensionslose
Zahl. Bei laminaren Strömungsproblemen muß man fordern, daß außer der geometrischen
Ähnlichkeit auch Ähnlichkeit bezüglich der Dicke der Grenzschicht besteht. Nach Gleichung
(17):
l1 D1
=
=
l2 D2
η1 l1
v1ρ1
η2 l2
v2ρ2
Daraus folgt, daß
v1ρ1l1 v2ρ2l2
η1 = η2
163
vρl
Re = η
Die dimensionslose Zahl
muß im ursprünglichen Problem und im Modell gleich groß sein, wenn die laminare viskose
Strömung korrekt modelliert werden soll. Die Reynoldszahl kann als Verhältnis der Trägheitseinflüsse ½ρv2 und der Reibungseinflüsse ηv/l aufgefaßt werden. Eine föllig reibungsfreie laminare Strömung ist instabil, da in einer zufälligen lokalen Verengung der Strömung nach
Bernoullli der Druck kleiner als in der Umgebung wird, so daß sich die Strömung weiter
Abb. 174: Eine kleine Störung in einer reibungsfreien Strömung verstärkt sich auf Grund des Bernoulli Effektes.
einschnürt. Dem wirkt die Viskosität entgegen, die Geschwindigkeitsunterschiede ausgleicht.
Wenn die viskosen Kräfte klein sind, entsteht Turbulenz, d.h. ein Gemisch von Wirbeln verschiedener Größe, wodurch der Reibungswiderstand erhöht wird. Der Umschlag von laminarer in turbulente Strömung erfolgt für eine gegebene Anordnung bei einer bestimmten
Reynoldszahl. Für Abschätzungen ist es manchmal gut, sich zu merken, daß der Umschlag bei
Re = 1000 erfolgt. Der genaue Wert der Reynoldszahl hängt natürlich davon ab, auf welche
charakteristische Länge man sie bezieht. Nimmt man die typische Größe von Wirbeln, erfolgt
der Umschlag bei Re ≈ 1.
Neben der Reynoldszahl gibt es in der Hydrodynamik eine ganze Reihe von dimensionslosen
Zahlen: Machzahl, Prandtlzahl, Pitotzahl, Picletzahl, für Probleme der Stoßwellenbildung, des
Wärmeübergangs an Oberflächen u.s.w. Oft führt die Forderung nach Einhaltung mehrerer
Ähnlichkeitsbedingungen zu Widersprüchen, so daß ein Modell nur gewisse Aspekte eines
physikalischen Problems simulieren kann.
164
KAPITEL F
Mechanik starrer Körper
1. Das Modell des starren Körpers
Der starre Körper ist ein Vielteilchensystem mit konstanten Abständen zwischen den Teilchen. In Realität gibt es keine volkommen starre Körper. Nach der Relativitätstheorie sind sie
sogar prinzipiell unmöglich, da man sonst Signale mit einer größeren Geschwindigkeit als der
Lichtgeschwindigkeit übertragen könnte. Für die Mechanik von Festkörpern ist der starre Körper ein gutes Modell, solange man sich nicht für elastische Verformungen, z.B. Wellen
interessiert.
Die Bewegung ist wie bei allen Vielteilchensystemen als Überlagerung einer Translation des
Schwerpunktes und einer Rotation um den Schwerpunkt zu beschreiben. Die Bewegungsgleichung zur Translation ist identisch mit der eines Massenpunktes, der sich am Ort des Schwerpunktes aufhält
•
F ext = m ges v s
(1)
vs ist die Schwerpunktsgeschwindigkeit mit
1
r s = m ∫ rdm
ges
m ges = ∫ dm
Die Rotation wird beschrieben durch
M = dL ,
dt
(2)
wobei M das gesamte äußere Drehmoment und L der Drehimpuls ist.
2. Statik
In der Statik bewegt sich der Körper nicht. Aus den Bewegungsgleichungen (1) und (2) folgt
dann mit dvs/dt = 0 und dL/dt = 0
Σ M i,ext = 0
(3)
165
Abb. 175: Zur Definition des Drehmomentes
und
Σ F i,ext = 0
(4)
Gleichung (3) ist das Hebelgesetz, wobei M = r × F . Für die Beträge heißt dies,
M = rFsinα = lF.
l = rsinα heißt der Kraftarm. Er ist nach Abb. 175 das Lot vom Drehpunkt auf die Kraftrichtung. Der Drehpunkt kann bei statischen Problemen beliebig gewählt werden. Man wählt
zweckmäßigerweise einen Angriffspunkt einer der Kräfte als Drehpunkt. Dadurch verschwindet das Drehmoment dieser Kraft.
Abb. 176: Die Drehrichtung der Garnrolle hängt von der
Richtung des Drehmomentes bezüglich des Auflagepunktes
ab.
Als Beispiel betrachten wir die Garnrolle in Abb. 176. Bei Fadenstellung (2) bewegt sie sich
nach rechts, bei Fadenstellung (1) nach links. Dies läßt sich sofort einsehen, wenn man den
Berührungspunkt A als Drehpunkt betrachtet. Nimmt man statt dessen den Mittelpunkt der
Rolle, muß man das Drehmoment durch die Reibungskraft an der Auflagestelle mit berücksichtigen. Zur vollständigen Lösung eines statischen Problems sind Gleichung (3) und (4)
erforderlich.
Beispiele:
In Abb. 177 ist nach den Auflagekräften F1 und F2 gefragt.
Lösung:
Der Drehpunkt sei die linke Auflage. Die Gleichungen für Gleichgewicht lauten dann
166
Abb. 177: Ein einfaches Problem der Statik: Wie
groß sind die Auflagekräfte?
Σ Fi = 0 :
F1 + F2 = FG
Σ Mi = 0 :
FGx = F1l
Man erhält zwei Gleichungen für die Unbekannten F1 und F2
F 2 = F G  1 − x 
l
F1 = FG x
l
Beispiel: Die angelehnte Leiter (Abb. 178).
Abb. 178: Wann fängt die angelehnte Leiter an zu
rutschen?
Man kann wieder nach den Auflagekräften fragen, außerdem nach dem Winkel α, bei dem die
Leiter anfängt zu rutschen. Die Grundgleichungen lauten:
Σ F = 0:
ΣM=0
F G = F1 + F4
F3 = F2
F G l cos α = F s l cos α + F 2 l sin α
2
Bei dem Grenzwinkel, bei dem die Leiter zu rutschen anfängt, sind die Reaktioskräfte gerade
gleich den Reibungskräften, die wegem Ft = µFN gegeben sind durch
167
F3 = F1µ1
F4 = F2µ2
Man erhält also fünf Gleichungen für die vier unbekannten Kräfte und den Grenzwinkel α.
Abb. 179: Eine Kugel in einer Mulde ist im
stabilen, auf einer Kuppe im labilen und auf
einer Ebene im indifferenten Gleichgewicht.
Abb. 180: Die Kiste ist im stabilen Gleichgewicht, obgleich sich der Schwerpunkt
oberhalb
der
unterstützenden
Fläche
Abb. 181: Zwei Fälle von labilem Gleichgewicht
Ob ein System im Gleichgewicht bleibt, muß durch eine Stabilitätsbetrachtung geklärt werden. Dazu entfernt man das System etwas aus der Gleichgewichtslage und sieht zu, ob es in
die Gleichgewichtslage zurückkehrt. Wenn ja, ist das System stabil, wenn die Abweichung
vom Gleichgewicht wächst, ist das System labil, sonst indifferent. Die Abbildungen 179- 181
zeigen einige Situationen zur Illustrierung der verschiedenen Gleichgewichtsbegriffe. In Abb.
181 b handelt es sich um ein dynamisches System, etwa ein in eine Drehbank eingespanntes
Kabel. Liegt dieses in der Achse des Drehfutters, befindet es sich im Gleichgewicht. Die
kleinste Ausbeulung führt zu Zentrifugalkräften, die bestrebt sind, die Ausbeulung zu
vergrößern.
3.Grundbegriffe zur Beschreibung einer Rotation
a) Das Trägheitsmoment
Bei der Rotation eines starren Körpers führen alle Teilchen eine Kreisbewegung mit der gleichen Winkelgeschwindigkeit ω aus. ω zeigt in Richtung der momentanen Drehachse, für die
wir im folgenden die z - Achse wählen. ω kann sich im Laufe der Bewegung relativ zum Körper oder im Raum ändern. Versuche mit dem Gyroskop und einem unsymmetrischen Kreisel
demonstrieren beide Effekte. Im folgenden wird vorrübergehend eine körper- und raumfeste
Achse angenommen.
168
Zur Berechnung der dynamischen Größen wird der Körper in Massenelemente ∆mi unterteilt.
Damit können die in Kapitel C.4 eingeführten Größen für die Drehbewegung eines Massenpunktes benutzt werden. Wenn Mi das Drehmoment auf das ite Massenelement ist, schreibt
sich die Bewegungsgleichung
•
•
M 1 + M 2 + ... = ∆m 1 r 21 ω + ∆m 2 r 22 ω +..
Da alle Massenelemente mit der gleichen Winkelgeschwindigkeit rotieren, kann man diese
ausklammern und erhält
•
M ges = J ω
Hierin ist
(5)
J = lim
∆m→0
Σ r 2i ∆m i = ∫ r 2 dm
(6)
das Trägheitsmoment bezüglich der betrachteten Achse. ri ist der Abstand des Massenelementes ∆mi von der Achse. Die Rotationsenergie ergibt sich zu
E rot = Σ 1 v 2i ∆m i = 1  Σ r 2i ∆m i  ω 2
2
2
E rot = 1 Jω 2
2
(7)
b) Der Drehimpulsvektor
Abb.182: Hier zeigt der Drehimpulsvektor nicht in Richtung der Drehachse
Für einen Massenpunkt gilt L = ms × v . L zeigt also im allgemeinen nicht in Richtung der
Drehachse (s. Abb. 182). Die Komponente des Drehimpulses in Richtung der Drehachse ist
L z = L sin α = msvsin α = mr 2 ω
169
Für einen kontinuierlichen Körper gilt daher
L z = ω ∫ r 2 dm = J (z) ω
Abb. 183: Bei axialsymmetrischen Körpern zeigt der
Drehimpuls entlang der Achse.
Ist der Körper symmetrisch, d.h. gehört zu jedem Massenelement ein zweites, das an dem zur
Achse gespiegelten Ort des Massenelementes liegt (Abb. 183), so sind L und ω parallel und es
gilt L = J(z)ω. Alle Achsen, für die dies gilt, heißen Hauptachsen. In der theoretischen Mechanik zeigt man, daß es für jeden Körper (also auch unsymmetrische Körper) drei Hauptachsen
gibt, die senkrecht aufeinander stehen. Die Trägheitsmomente der Hauptachsen heißen Hauptträgheitsmomente. Die Trägheitsmomente für alle anderen Richtungen werden durch ein Ellipsoid beschrieben, dessen Hauptachsen die Hauptträgheitsachsen sind (Abb. 184).
Abb. 184: Das Trägheitsmoment für die Achse a ergibt
sich aus dem Trägheitsellipsoid.
Beispiele:
Abb. 185: Der Zylinder hat eine Symmetrieachse.
Das Trägheitsellipsoid ist ein Rotationsellipsoid. Der
Würfel hat drei Symmetrieachsen. Das Trägheitsellipsoid ist eine Kugel
Bei einer Kugel bilden drei beliebige senkrecht zueinander stehende Achsen Hauptträgheitsachsen. Das Trägheitsellipsoid ist eine Kugel.
170
Bei einem Zylinder ist die Figurenachse eine Hauptträgheitsachse. Allgemein ist eine Symmetrieachse eines Körpers eine Hauptträgheitsachse, wie aus der Definition der Hauptträgheitsachse zu ersehen ist. Die andern beiden Achsen stehen senkrecht zu dieser Achse und senkrecht zueinander, aber sonst beliebig.
Abb. 186: Modell der Unwucht
Bei der Rotation eines Körpers um eine Achse, die nicht Hauptachse ist, werden aufgrund der
Zentrifugalkräfte zusätzliche Kräfte auf die Lager der Achse ausgeübt. (Ohne diese müßte L
nach dem Drehimpulssatz raumfest bleiben). Der Körper ist nicht ausgewuchtet. Der Drehimpuls ergibt sich für
ω = ωxex + ωyey + ωzez
L = J (x) ω x e x + J (y) ω y e y + J (z) ω z e z
Die Bewegungsgleichung für die Rotation (Gleichung (5)) schreibt sich vektoriell
•
M =L
(8)
Man beachte: Es gibt in der Natur einen kleinsten Betrag für den Drehimpuls
L min = 1 h
2 2π
! = h/2π = 10
-34
kgm2/s ist das Plancksche Wirkungsquantum.
c) Berechnung des Trägheitsmomentes
α) Das Integral zur Berechnung des Trägheitsmomentes
Für einen homogenen Körper lohnt es sich, die konstante Dichte ρ einzuführen.
∆m = ρ∆V
171
Abb. 187: Bei homogenen Körpern berechnet man das
Trägheitsmoment über ein Volumenintegral.
Das Trägheitsmoment wird dann eine geometrische Größe:
J = ρ ∫ r 2 dm
Die Berechnung des Integrals gestaltet sich im allgemeinen als schwierig. Ein wichtiger erster
Schritt besteht daher darin, ein geeignetes Koordinatensystem auszuwählen. Für kartesische
Koordinaten, in denen die z - Achse die Drehachse ist, hat das Integral die explizite Form
J = ρ ∫ ∫ ∫ (x 2 + y 2 )dxdydz
Zur Lösung des Integrals wird wie bei der Berechnung des Schwerpunktes nacheinander eine
der Ortsvariablen variiert, die übrigen konstant gelassen. Dabei berücksichtigt man, daß die
Integrationsgrenzen, die durch die Berandung des Körpers gegeben sind, von den konstant gelassenen Variablen abhängen können. Bei zusammengesetzten Körpern kann man die Trägheitsmomente der Einzelteile addieren. Man beachte, daß die Größe des Trägheitsmomentes
von der Lage der Achse abhängt. Die gesamte Information über alle Trägheitsmomente eines
Körpers steckt in den Hauptträgheitsmomenten und dem Abstand der Drehachse vom
Schwerpunkt.
β) Beispiele
i. Dünnwandiges Rohr, die Drehachse ist die Figurenachse
Abb. 188: Das Trägheitsmoment eines dünnwandigen Rohres ergibt sich ohne Rechnung.
Teile das Rohr in beliebige Massenelemente ∆m. Alle haben den gleichen Abstand R zur
Drehachse.
172
J = lim
∆ →
Σ R 2 ∫ dm = R 2 ∫ dm = R 2 m ges
ii. Kreisscheibe, Drehachse ist die Figurenachse
Abb. 189 und 190: Das Volumenelement bei
der Berechnung des Trägheitsmomentes einer
Kreisscheibe bez. der Figurenachse.
Man wähle Zylinderkoordinaten, d.h. man unterteile die Scheibe durch Schnitte r = const,
ϕ = const und z = const, im Abstand ∆r, ∆ϕ und ∆z. Das Volumenelement hat die Größe
∆V = ∆r∆z(r∆ϕ)
Das zu lösende Integral wird
J = ρ ∫ ∫ ∫ r 3 drdϕdz
Im ersten Schritt wird über z integriert, wobei r und ϕ konstant bleiben.
Abb.191: Das Volumen nach der Integration über z.
D
J = ρ ∫ ∫  ∫ dz  r 3 drdϕ = ρD ∫ ∫ r 3 drdϕ
0
D ist die Dicke der Scheibe. Im zweiten Schritt wird über ϕ integriert, wobei r konstant gelassen wird.
Abb. 192: Das Volumen nach der Integration über
ϕ. Bis hier her kommt man ohne Rechnung aus.
173
R
2π
J = ρD ∫  ∫ dϕ  r 3 dr = 2πρD ∫ r 3 dr
0
0
Dieses Zwischenergebnis hätte man auch direkt hinschreiben können, wenn man eine ringförmige Unterteilung der ursprünglichen Scheibe vorgenommen hätte. Das Trägheitsmoment eines Ringes ist dann dJ = ρ2πrdrDr2. Im dritten Schritt wird über r integriert.
4
J = πρD R
2
An dieser Stelle ist es von Vorteil, die Gesamtmasse des Körpers einzuführen: mges = ρπR2D
J = 1 m ges R 2
2
iii. Dünne Kreisscheibe, Achse liegt in der Ebene der Scheibe.
Abb. 193: Jetzt liegt die Drehachse in der Kreisscheibe.
Angpaßte Koordinaten wären Polarkoordinaten. Zu Übungszwecken wird mit kartesischen
Koordinaten gerechnet. Die y - Achse sei die Drehachse. Das Volumenelement ist
dV = dxdydz. Der Abstand zwischen der Drehachse und dem Volumenelement ist x, die Dicke
der Scheibe wieder D.
Die Integration über z ist trivial. Die Integration über y erstreckt sich von yu bis yo, welche
Funktionen von x sind, die die Form der Berandung beschreiben
yo
J (y) = ρ ∫ ∫ ∫ x 2 dxdydz = ρD ∫  ∫ dy  x 2 dx = ρD ∫ (y o − y u )x 2 dx
yu
Die Funktionen der Berandung folgen aus der Kreisgleichung
174
yo = R2 − x2
yu = − R2 − x2
Das letzte Integral hat dann die Form
J (y) = 2ρD ∫
+R
−R
x 2 R 2 − x 2 dx = 2ρDR 3 ∫
+R
−R
x 2 1 − x 2 dx
R2
R2
Zur weiteren Vereinfachung wird substituiert: x = sin ϕ
R
x = -R → ϕ = − π/2
wobei die Grenzen geändert werden:
x = +R → ϕ = + π/2
dx = Rcosϕdϕ
und
Bei dieser Substition wird eigentlich nichts anderes gemacht, als die Koordinate x durch die
besser angepaßte Koordinate ϕ zu ersetzen. Hätte man gleich am Anfang die Koordinaten r
und ϕ eingeführt, hätte man sich diesen Rechenschritt gespart. Das Integral hat nun die Form
I=R∫
+π/2
−π
sin 2 ϕ cos 2 ϕdϕ
Die Quadrate wird man los, indem man zum doppelten Winkel übergeht
2sinϕcosϕ = sin2ϕ
sin22ϕ = ½(1-cos4ϕ)
+π/2
I = 1R ∫
(1 − cos 4ϕ)dϕ = π R
−π/2
8
8
J (y) = π ρDR 4 = 1 m ges R 2
4
4
Das gleiche Ergebnis kann ohne viel Rechnerei aus einer Symmetriebetrachtung gewonnen
werden. Für flächige Körper gilt
J (z) = ∫ (x 2 + y 2 )dm = J (x) + J (y)
175
Ist der Körper wie im Fall der Kreisscheibe symmetrisch bezüglich Vertauschung von x und y,
gilt J(x) =J(y), daher J(z) = 2J(y). Da J(z) = ½mgesR2, folgt sofort J (y) = 1 m ges R 2 .
4
γ) Der Satz von Steiner
Das Trägheitsmoment bezüglich einer Achse z*, die nicht durch den Schwerpunkt geht, kann
auf das Trägheitsmoment bezüglich einer Achse z, die durch den Schwerpunkt geht und zu z*
parallel ist, zurückgeführt werden (s. Abb. 194).
Abb. 194: Transformation zur Ableitung des Satzes von Steiner.
J ∗ = ∫ r ∗2 dm = ∫ (r − a) 2 dm = ∫ (r 2 − 2a • r + a 2 )dm = ∫ r 2 dm + ∫ a 2 dm − 2a • ∫ rdm
Da r vom Schwerpunkt aus gerechnet wird, ist r s = ∫ rdm = 0. Daraus folgt der Satz von
Steiner
(9)
J∗ = Js + a2m
δ) Trägheitsmomente einiger Körper. Abb. 195 - 198:
J = 1 mR 2
2
2
2
J = m  R + L 
4 12
2
2
J = m  l + b 
12
J = 2 mR 2
5
176
4. Beispiele zur Bewegung starrer Körper
Im folgenden werden Bewegungen betrachtet, bei denen die Drehung eines Körpers eine Rolle
spielt. Im wesentlichen handelt es sich um Anwendungen der Gleichung (8). Einige der Beispiele wurden schon früher einmal behandelt, wobei dann der Effekt der Drehung vernachlässigt wurde. Z.B. wurden Versuche an der schiefen Ebene immer mit rollenden Körpern durchgeführt, aber es wurde argumentiert, als ob die Körper reibungsfrei rutschten. Wir werden
jetzt sehen, wie die Überlegungen modifiziert werden müssen und in wieweit die früheren Betrachtungen berechtigt waren.
a) Achse ist raum - und körperfest, das äußere Drehmoment ist konstant
Abb. 199: Die Atwoodsche Fallmaschine. Die Trägheit der
Rolle wird mit berücksichtigt.
Als Beispiel wird die Atwoodsche Fallmaschine mit Berücksichtigung des Trägheitsmomentes
der Rolle behandelt (Abb. 199). Man muß bedenken, daß die Kräfte, die der Faden auf die
Rolle ausübt, nicht einfach die Schwerkräfte der Massen m1g und m2g sind, wie man sich klar
machen kann, wenn man in Gedanken die Fäden oberhalb der Masse durchschneidet. Diese
Kräfte werden also als Unbekannte F1 und F2 angesetzt.
Drehung der Rolle
•
(F 1 − F 2 )R = J ω
(10)
Translation von m1 und m2
•
•
m1g − F1 = m1 v1 = m1R ω
•
m 2 g − F 2 = −m 2 R ω
Diese Gleichungen werden nach F1 und F2 aufgelöst und in Gleichung (10) eingesetzt
 m 1 g − m 1 R ω• −m 2 g − m 2 R ω•  R = J ω•


177
•
(m 1 − m 2 )g =  J + (m 1 + m 2 )R  ω
R

•
ω = α0 =
(m 1 − m 2 )gR
J + (m 1 + m 2 )R 2
Durch Integration erhält man wie bei der geradlinigen Bewegung unter konstanter Kraft
ω = α0t + ω0
ϕ = ½α0t2 + ω0t + ϕ0
•
•
Diskussion: Für J << (m1 + m2)R2 wird (m 1 + m 2 )R ω= (m 1 + m 2 ) v = (m 1 − m 2 )g. Die antreibende Kraft ist (m1 - m2)g, die träge Masse m1 + m2. Für J >> (m1 + m2)R2 wird
•
(m 1 − m 2 )gR = J ω . Die Trägheit des Systems ist nur durch die Scheibe bestimmt. Das äußere
Drehmoment ist (m1 - m2)gR. (m1 + m2)R2 ist das Trägheitsmoment der an den Fäden hängenden Massen. Die Kraft auf das Lager kann aus der Kräftebilanz berechnet werden:
F1 + F2 + msg = FL
Hierin ist ms die Masse der Scheibe und FL die Kraft auf das Lager.
b) Achse körperfest, Hauptträgheitsachse, wird bei der Bewegung parallel verschoben
Als Beispiel wird die Walze auf einer schiefen Ebene betrachtet (Abb. 200). Hier darf die tangentiale Reaktionskraft F1 nicht vergessen werden. Das Vorhandensein einer solchen Kraft erkennt man, wenn man sich den Grenzfall verschwindender Reibung vorstellt. Die Bewegungsgleichung setzt sich wieder aus einem Anteil für Translation und einem für Rotation
zusammen
Abb. 200: Beim Herabrollen spielt das Trägheitsmoment
eine Rolle.
Translation:
Rotation
•
m v = Ft − F1
•
•
F 1 R = J ω == J v
R
178
Die Variablen v und ω hängen über die Abrollbedingung voneinander ab. Im Schwerpunktsystem der Rolle ist die Geschwindigkeit der Unterlage v = ωR. Daher ist im Laborsystem v die
Geschwindigkeit der Rolle. Elimination von F1 ergibt
•
•
m v = mgsinα − J2 v
R
 1 + J  v• = gsinα

mR 2 
Da J = ½mR2 ist J/(mR2) = 1/2. Die Bewegung ist von der Masse und vom Radius unabhängig.
g
= 2 g ersetzt wäre. Bei gleicher Masse aber ungleichmäSie läuft so ab, als ob g durch
J
1+ 2 3
ßiger Massenverteilung wird eine Walze, die ein größeres Trägheitsmoment besitzt, zu jedem
Zeitpunkt langsamer laufen. Diese Tatsache kann man aus dem Energiesatz direkt ablesen.
Die potentielle Energie wird im Anfangspunkt Null gesetzt. Zählt man die vertikale Koordinate y nach unten positiv, heißt der Energiesatz
−ymg + 1 mv 2 + 1 Jω 2 = 0
2
2
1  m + J  v 2 = mgy
2
R2 
Man erkennt, daß anstelle der Masse bei der reinen Translation die Größe m + J2 auftritt, Diese Größe kann man als effektive träge Masse auffassen.
c) Achse körperfest, Hauptträgheitsachse, kein äußeres Drehmoment
Man erreicht eine solche Situation durch eine Cardanische Aufhängung (Abb. 201).
•
Da L = J (z) ω und M =L , und nach Vorraussetzung M = 0, bleibt L konstant. L und damit ω
behalten die Richtung bei. Diese Aufhängung des Kreisels wird zur Richtungskontrolle oder
-anzeige z.B. im künstlichen Horizont benutzt.
Abb. 201: Cardanische Aufhängung eines Kreisels
179
d) Körperfeste Achse,die eine Hauptträgheitsachse ist; Drehmoment senkrecht zu L
Abb. 202: Die Reaktion eines Kreisels auf eine äußere Kraft
•
Auf den Kreisel in Abb. 202 soll die Kraft F wirken. M und damit wegen M =L die Änderung
des Drehimpulses ∆L stehen senkrecht auf F. Der Kreisel weicht seitlich aus, da sich die
Drehachse auf den neuen Wert L + ∆L einstellt. Wird das Drehmoment durch das eigene Gewicht des Kreisels erzeugt (Abb. 203), ergibt sich ein dL, das immer senkrecht auf dem momentanen L steht. Die Kreiselachse umläuft einen Kegelmantel. Man sagt, er vollführt eine
Präzessionsbewegung. Die Präzessionsfrequenz ωp ergibt sich aus
dϑ =
dL
L sin α
dϑ = ω = dL 1 = M
p
dt L sin α L sin α
dt
Abb. 203: Die Präzession des Kreisels
Man kann diesen Zusammenhang auch vektoriell schreiben
M = ωp × L
Umgekehrt übt ein Kreisel, der zu einer Präzessionsbewegung gezwungen wird, z.B. die Kurbelwelle im Motor bei Kurvenfahrt, ein Drehmoment auf die Lager aus
M K = −M = L × ω p
180
Abb. 204: Ein oberhalb des Schwerpunktes unterstützter
Kreisel präzediert in umgekehrter Richtung
Dies bewirkt in kleinen Motorflugzeugen eine zusätzliche Auf - oder Abwärtsbewegung bei
Kurvenfahrt. Unterstützt man einen Kreisel oberhalb des Schwerpunktes, oder kehrt man die
Drehrichtung um, so kehrt sich die Richtung der Präzession um. Wegen der Abweichung der
Erde von der Kugelgestalt übt die Anziehung der Sonne auf diese ein Drehmoment aus. Dies
führt zu einer Präzession der Erdachse mit einer Umlaufperiode von 26000 Jahren.
Eine andere Erklärung für die Präzession
Abb. 205: Die Präzession kann man auch mit der Corioliskraft erklären.
Um die Präzession des Kreisels von einer anderen Seite zu beleuchten, betrachten wir die
Kräfte, die ein Kreisel auf seine Lager ausübt, wenn er eine Präzession beschreibt. Statt des
vollen Kreisels betrachten wir einen Ring. Da sich jeder axialsymmetrische Kreisel aus Ringen zusammensetzen läßt, können wir unsere Ergebnisse auf einen beliebigen axialsymmetrischen Kreisel erweitern. Zur Vereinfachung des Problems wird angenommen, die Rotationsachse L steht senkrecht auf der Präzessionsachse ωp. Die Situation ist die gleiche wie bei
einem Zug, der längs eines Meridians um die Erde fährt. Durch die Corioliskraft erfährt er eine Ablenkung senkrecht zur Fahrtrichtung, die auf der Nordhalbkugel nach rechts, auf der
Südhalbkugel nach links zeigt. Dies bewirkt also ein Drehmoment das senkrecht zu ωp und L
steht, wie wir es auch aus den Kreiselgesetzen gefolgert haben.
181
e) Anwendungen der Kreiselgesetze
α) Wendeanzeiger
Abb. 206: Der Wendeanzeiger.
Die Aufhängung ist in Abb. 206 angedeutet. Da die Drehachse versucht, sich in die neue
Richtung L + ∆L zu orientieren, werden Kurven, d.h. Drehungen um die vertikale Achse
angezeigt.
β) Der Kreiselkompaß
Abb. 207: Der Kreisel im Kreiselkompaß erhält ein Drehmoment nach Norden.
Hier ist der Kreisel so gelagert, daß die Achse immer horizontal, also parallel zur Erdoberfläche liegt. Durch die Erdrotation entsteht ein Drehmoment auf die Lager, das den Kreisel in die
Nord - Südrichtung auszurichten versucht. Zur Vermeidung von Schwingungen muß die Bewegung um die vertikale Achse gedämpft werden.
γ) Spielkreisel
Der klassische Spielkreisel (Peitschen Top) ist in Abb. 208 dargestellt. Wir nehmen an, er
stellt sich durch eine Störung schräg. Wegen des endlichen Krümmungsradius an der Spitze
rollt.
Abb. 208: Der klassische Spielzeugkreisel richtet sich auf
rollt
diese am Boden ab. Da der Schwerpunkt ungefähr im Raum stehen bleibt und oberhalb des
Krümmungsmittelpunktes der Kugelfläche der Spitze liegt, zeigt L × ω p in eine Richtung, die
182
das Aufrichten des Kreisels bewirkt (Abb. 208). Der Umkehrkreisel (Abb.209) rollt umgekehrt auf dem Boden ab, da sei Schwerpunkt unterhalb vom Krümmungsmittelpunkt liegt.
Abb. 209: Der Umkehrkreisel
δ) Dynamische Stabilisierung des Fahrrads
Das Fahrrad erfährt durch die Kreiselgesetze eine gewisse Stabilisierung. Wenn es umzukippen droht (Abb. 210), entsteht ein Drehmoment M, das eine Lenkung in Kipprichtung bewirkt. Dieser Lenkeinschlag wirkt dem Kippen entgegen.
Abb. 210: Die Kreiselkräfte auf die Räder bewirken
beim Fahrrad eine gewisse Stabilisierung
183
KAPITEL G
Schwingungen
1. Allgemeines
Schwingungen sind Vorgänge, die sich wiederholen. Sehr viele physikalische Systeme können
Schwingungen ausführen. Neben den bekannten mechanischen Systemen wie Pendel, Schallerzeuger und Wassersäulen schwingen Moleküle, elektronische Schaltungen, Sterne (z.B. δ
Cepheiden) möglicherweise das ganze Weltall. Oft ist die Schwingung eines Signals mit der
Rotation von Quelle oder Empfänger verbunden wie bei der Helligkeit des Tageslichts oder
bei Pulsaren, Sternen, die von diskreten Stellen ihrer Oberfläche Radiosignale aussenden.
Schwingungen werden für die Zeitmarkierung z.B. in Uhren und Oszillographen, in Radiosendern, Musikinstrumenten und vielen anderen Systemen angewendet. Sie bilden die Grundelemente von Wellen. Die Schwingungslehre bildet daher die Grundlage der Lichttheorie.
Eine streng periodische Schwingung wiederholt sich nach der Periodendauer T:
f(t) = f(t + T)
2. Die harmonische Schwingung
a) Darstellung
Die einfachste periodische Schwingung ist die harmonische, in der sich eine physikalische
Größe sinusförmig mit der Zeit ändert.
x(t) = x 0 sin (ωt + ϕ 0 )
(1)
x kann irgendeine physikalische Größe sein wie die Ortskoordinate, der Druck, die Temperatur, Feldstärke und vieles mehr. In Gleichung (1) ist x der Momentanwert dieser Größe, |x0|
das Maximum nennt man die Amplitude, ω = 2π/T = 2πf die Kreisfrequenz und (ωt + ϕ0) die
Phase. Die Phase wird wie ein Winkel im Bogenmaß gemessen und variiert während einer Periode von 0 bis 2π. ϕ0 ist die Anfangsphase, d.h. die Phase zur Zeit t = 0.
Beliebige periodische Schwingungen kann man aus der Überlagerung von harmonischen
Schwingungen zusammensetzen. Man kann die harmonische Schwingung darstellen als Projektion einer gleichförmigen Kreisbewegung eines Punktes (Abb. 211).
184
Abb. 211: Die harmonische Schwingung kann als
Projektion einer Kreisbewegung aufgefaßt werden.
x = x 0 cos (ϕ + ϕ 0 ) = x 0 cos (ωt + ϕ 0 ) = x 0 [cos ωt cos ϕ 0 − sin ωt sin ϕ 0 ]
Abb. 212: Statt der Zeit, die in einer Periode von 0 bis T läuft, kann man auch
die Phase, die von 0 bis 2π läuft, als unabhängige Variable nehmen.
Statt der beiden unabhängigen Parameter x0 und ϕ0 kann man
A = x 0 cos ϕ 0 und
B = −x 0 sin ϕ 0
(2)
einführen. Dadurch ergibt sich die zu Gleichung (1) äquivalente Form
x = A cos ωt + B sin ωt
(3)
Dies heißt, daß jede harmonische Schwingung als Überlagerung einer unverschobenen Sinus und einer unverschobenen Kosinusschwingung gleicher Frequenz dargestellt werden kann.
Insbesondere ist nach Gleichung (2) und (3) cos(ωt−π/2) = sinωt, eine Beziehung die sich direkt aus der Definition am rechtwinkligen Dreieck ablesen läßt. Eine Kosinusschwingung ist
eine phasenverschobene Sinusschwingung. Die Darstellung durch komplexe Zahlen lernen wir
im Abschnitt 4. dieses Kapitels kennen.
b) Die Kinematik der harmonischen Schwingung
Wir setzen eine harmonische Schwingung der Form
x = x 0 cos (ωt + ϕ 0 )
voraus und ermitteln durch Differentiation den zeitlichen Verlauf von Geschwindigkeit und
Beschleunigung
185
•
v = x = −x 0 ω sin (ωt − ϕ 0 )
••
a = x = −x 0 ω 2 cos (ωt + ϕ 0 )
Die Geschwindigkeitsamplitude ist v0 = x0ω, die Beschleunigungsamplitude a0 = x0ω2 . Die
Phasenverschiebung zwischen v und x ist π/2. Durch Aufzeichnen der Funktionen x(t) und v(t)
z.B. für ϕ0 = 0 stellt man fest, daß das Maximum von v vor dem von x erreicht wird, wenn
man die sich am nächsten liegenden Maxima vergleicht. Man sagt, v eilt vor x. Die Phasenverschiebung zwischen a und x beträgt π. Man kann also für die Momentanwerte schreiben
a(t) = - ω2x(t), und damit
••
x = − ω2x
(4)
Bei einer harmonischen Schwingung eines physikalischen Systems gilt für die schwingende
Größe eine Differentialgleichung der Form von Gleichung (4), die sogenannte Schwingungsgleichung. Umgekehrt kann man sagen, daß ein System eine Schwingung ausführen kann,
wenn sich für eine physikalische Größe x , die das System bestimmt, eine Gleichung der Form
(4) aufstellen läßt.
c) Die Schwingung eines Massenpunktes
α) Allgemeine Betrachtung
Für den Schwerpunkt eines Körpers, der sich auf einer beliebigen Kurve bewegen kann, gilt
die Bewegungsgleichung
••
m s = Ft
wenn Ft die zur Kurve tangentiale Kraft ist. Damit sich hieraus eine Schwingungsgleichung
der Form von Gleichung (4) ergibt, muß die Kraft eine Abhängigkeit
Ft = -Ds
(5)
von der Koordinate auf der Bahn haben. Die Schwingungsgleichung lautet dann
186
••
s = −D
ms
Der Körper kann also eine harmonische Schwingung ausführen mit der Kreisfrequenz
ω=
D
m
(6)
In vielen praktischen Fällen liegt nicht das einfache Kraftgesetz von Gleichung (5) vor. Häufig kann man dann aber noch F(s) durch eine Taylorentwicklung linearisieren, so daß wenigstens für kleine Auslenkungen s F(s) = - Ds gilt. Die Schwingung ist dann nue für kleine Auslenkungen harmonisch.
β) Energieverhältnisse
Da nach den Gleichungen (5) und (6) F = - mω2s gilt, erhält man für die potentielle Energie
x
W pot = −∫ F(s)ds = 1 mω 2 x 2
0
2
und
W kin = 1 mv 2
2
Setzt man x = x0sin(ωt + ϕ0) und v = x0 ωcos(ωt + ϕ0), erhält man
W ges = W pot + W kin = 1 mω 2 x 20 sin 2 (ωt + ϕ 0 ) + 1 mω 2 x 20 cos 2 (ωt + ϕ 0 ) = 1 mω 2 x 20
2
2
2
Die Gesamtenergie ist also unabhängig von der Zeit, wie der Energiesatz der Mechanik für
dissipationsfreie Systeme fordert. Die Energie des Systems wechselt zwischen kinetischer und
potentieller Energie. Bei Schwingungen hat man generell zwei Energieformen, die das System
annehmen kann, z.B. elektrische und magnetische Feldenergie. Um eine harmonische Schwingung eines Körpers zu erhalten, muß die potentielle Energie einen parabelförmigen Verlauf
Wpot = ½mω2x2. besitzen.
Abb. 213: Vorraussetzung für eine harmonische
Schwingung ist ein parabelförmiges Potential.
187
Bei nicht parabelförmigen Potentialtöpfen erhält man keine harmonische Schwingung. Solange Wpot + Wkin = const gilt, ist diese aber noch periodisch, wie man sich an der Bewegung einer Kugel in dem entsprechenden Potentialtopf klar macht. Für kleine Amplituden lassen sich
die meisten Potentialmulden durch eine Parabel annähern, so daß dann eine harmonische
Schwingung resultiert.
γ) Das Federpendel
i. Die Schwingungsgleichung
Abb.214: Das Federpendel
Eine Masse m hänge an einer elastischen Feder, für die FF = - Dx gilt. x wird von der Stellung,
bei der die Feder entspannt ist, gemessen. Auf m wirkt außerdem die Schwerkraft FG = mg. In
der Ruhelage x0 gilt F = FF + FG = 0. Daraus folgt Dx0 = mg und daher bei beliebiger
Auslenkung
F(x) = -D(x0 + ξ) +mg = -Dξ
wobei ξ die Auslenkung aus der Gleichgewichtslage ist. Das Kraftgesetz für die Auslenkung
aus der Gleichgewichtslage mit Schwerkraft ist also das gleiche wie das für die Auslenkung
der entspannten Feder ohne Schwerkraft. Die Bewegungsgleichung lautet damit
••
m ξ = −Dξ
und die Schwingungsgleichung
••
ξ = −D
mξ
Die Masse schwingt also harmonisch um die Gleichgewichtslage.
(6)
188
ii. Bestimmung der Frequenz
Wir machen den Ansatz ξ = sinωt und bilden die zweite Ableitung, um mit dem Ansatz in die
Schwingungsgleichung zu gehen
•
ξ = ω cos ωt
••
ξ = −ω 2 sin ωt
Einsetzen in Gleichung (6) ergibt
ω2 = D
m
Die allgemeine Lösung lautet
ξ = A sin ωt + B cos ωt oder ξ = ξ 0 cos (ωt + ϕ 0 )
iii. Bestimmung der Konstanten
Wir betrachten als Beispiel die erste Form der Lösung und bestimmen die Konstanten A und
B aus den Anfangsbedingungen. Zur Zeit t = 0 sei die Auslenkung ξ = ξ0 und v = v0. Einsetzen ergibt
ξ0 = Asin(0) + Bcos(0)
Daraus folgt sofort B = ξ0.
v0 = Aωcos(0) - Bωsin(0)
Daraus folgt A = v0/ω. Die Lösung hat also die Form
v
ξ = ω0 sin ωt + x 0 cos ωt
Für den Sonderfall, v0 = 0, d.h die Situation, in der die Masse anfangs ausgelenkt und dann
losgelassen wurde, erhält man eine reine Kosinusschwingung, wobei die Anfangsauslenkung
die Amplitude bestimmt.
d) Die Schwingung eines ausgedehnten Körpers (Das physikalische Pendel)
189
Für die Drehschwingung eines ausgedehnten Körpers mit dem Drehwinkel θ um eine feste
Achse gilt die Bewegungsgleichung
•
••
M=Jω =Jθ
Wenn M = -kθ ist, ergibt sich die Schwingungsgleichung
••
θ = −kθ
J
Beispiel: Das physikalische Pendel
Abb. 215: Zur Aufstellung der Schwingungsgleichung eines ausgedehnten Körpers geht man von der Bewegungsgleichung für eine Drehung aus.
Nach Abb. 215 ist l der Abstand zwischen Drehpunkt und Schwerpunkt. Dann gilt für das
Drehmoment
M = mglsinθ
Die Bewegungsgleichung hat die Form
••
−mgl sin θ = J θ
Und die Schwingungsgleichung
••
θ =−
mgl
sin θ
J
Da J ~ m, ist die Bewegung von der Masse des Körpers unabhängig. Die Schwingungsgleichung ist nicht die der harmonischen Schwingung. Für kleine Auslenkungen gilt die lineare
Näherung sinθ = θ. Und die Schwingung ist harmonisch.
190
••
mgl
θ
J
Das Pendel schwingt harmonisch mit der Kreisfrequenz
θ =−
ω=
mgl
J
Das Pendel schwingt nur, wenn l ≠ 0. Der Schwerpunkt liegt also nicht im Drehpunkt, aber für
die Bewegung ist das Trägheitsmoment in Bezug auf den Drehpunkt maßgeblich. Dieses kann
mit dem Satz von Steiner auf das Trägheitsmoment in Bezug auf den Schwerpunkt Js zurückgeführt werden.
J = Js + l2m
Für die Kreisfrequenz erhält man dann
ω2 =
Wenn
Js
2
mgl
g
= ⋅
2
Js + l m l
1
+1
2
Js
(8)
<< 1 d.h. das Trägheitsmoment bezüglich einer Drehung um den Schwerpunkt sehr
viel kleiner als das Translationsträgheitsmoment ml2 ist, wird der zweite Faktor gleich eins
und es ergibt sich die Näherung des mathematischen Pendels
ω=
g
l
Eine Taylorentwicklung der exakten Formel Gleichung (8) führt zu
ω≈
g
1 − 1 J 2 
2 ml
l 
1 J s gibt die Korrektur dafür an, daß der Körper bei der Pendelbewegung des Schwerpunk2 2
tes gleichzeitig eine Drehung um den Schwerpunkt vollführt (Abb. 216).
191
Abb. 216: Die Masse an einem Faden führt eine Translationsbewegung,
d.h eine Pendelbewegung des Schwerpunktes und eine Rotation um den
Schwerpunkt durch.
3. Überlagerung von harmonischen Schwingungen gleicher Frequenz
a) Anwendung der Additionstheoreme
Sollen zwei Schwingungen gleicher Frequenz
x1 = A1cos(ωt + ϕ1)
x2 = A2cos(ωt + ϕ2)
addiert werden, was physikalisch durch die Addition der Drucke von zwei Schallwellen auf
dem Trommelfell oder der Feldstärke zweier elektromagnetischer Wellen auf einem Lichtdetektor realisiert wird, müssen zu jeder Zeit die Momentanwerte der Schwingungen addiert
werden.
x res = x 1 (t) + x 2 (t) = A 1 cos (ωt + ϕ 1 ) + A 2 cos (ωt + ϕ 2 )
= A 1 cos ϕ 1 cos ωt − A 1 sin ϕ 1 sin ωt + A 2 cos ϕ 2 cos ωt − A 2 sin ϕ 2 sin ω
Abb. 217: Man addiert zwei Schwingungen, indem
man ihre Momentanwerte addiert.
xres hat also die Form x res = B 1 cos ωt − B 2 sin ωt
mit
(9)
B 1 = A 1 cos ϕ 1 + A 2 cos ϕ 2
B 2 = A 1 sin ϕ 1 + A 2 sin ϕ 2
Die Terme der Gleichung (9) können wieder zusammengefaßt werden zu der Form
192
x res = A res cos (ωt + ϕ res )
mit
B 1 = A res cos ϕ res
B 2 = A res sin ϕ res
Durch Addieren und Quadrieren der letzten Gleichungen ergibt sich
A 2res = B 21 + B 22 = (A 1 cos ϕ 1 + A 2 cos ϕ 2 ) + (A 1 sin ϕ 1 + A 2 sin ϕ 2 )
2
2
(10a)
Durch Division dieser beiden Gleichungen
tan ϕ res =
B 1 A 1 sin ϕ 1 + A 2 sin ϕ 2
=
B 2 A 1 cos ϕ 1 + A 2 cos ϕ 2
(10b)
Die Überlagerung zweier harmonischer Schwingungen gleicher Frequenz ergibt also wieder
eine harmonische Schwingung dieser Frequenz. Amplitude und Phase kann man im Prinzip
durch die Gleichungen (10a) und (10b) ermitteln. Zweckmäßiger ist im allgemeinen die Verwendung eines Zeigerdiagramms.
b) Zeigerdiagramm
Abb. 218: Die Formeln für die Addition
zweier harmonischer Schwingungen lassen
sich am Zeigerdiagramm ablesen.
Die Umrechnungsformeln lassen sich an einem Zeigerdiagramm der Gestalt von Abb. 218 ablesen. Man erkennt dies an der Darstellung einer Schwingung als Projektion eines sich drehenden Zeigers. Sollen zwei Schwingungen addiert werden, müssen ihre Momentanwerte, d.h. die
Momentanwerte ihrer Projektionen addiert werden. Man kann statt dessen zunächst die beiden
Zeiger nach den Regeln der Vektoraddition addieren und von dem resultierenden Zeiger die
193
Projektion bilden. Dies wird in Abb. 218 für den Zeitpunkt t = 0 vorgenommen. Für spätere
∼
∼
Zeitpunkte ändert sich die Figur nicht, da sich die Zeiger A 1 und A 2 mit gleicher Drehzahl
drehen. Man ordnet also einer Schwingung einen Zeiger zu, indem man als Länge des Zeigers
die Amplitude der Schwingung, als Winkel mit der x - Achse die Anfangsphase wählt. Man
addiert diese Zeiger wie Vektoren.
c) Beispiele
i. Zwei Schwingungen gleicher Amplitude haben eine Phasenverschiebung von π. Wie groß
ist die Amplitude der aus ihrer Überlagerung resultierenden Schwingung?
Abb. 219: Die beiden Zeiger sind um 180° zueinander gedreht.
Sie
repräsentieren
damit
zwei
Wellen
mit
180°
Aus dem Zeigerdiagramm Abb. 219 ist abzulesen, daß
∼x res = ∼x 1 + ∼x 2 = 0
Die Überlagerung zweier Wellen kann also zum Verschwinden jeglicher Wellenbewegung
führen. Diesen Fall nennt man destruktive Interferenz.
ii. Zwei Schwingungen x1 = 3cosωt und x2 = 4sinωt sollen addiert werden. Welche Amplitude
und welche Phasenverschiebung gegen x1(t) hat die resultierende Schwingung?
Abb. 220: Das Zeigerdiagramm für die Überlagerung zweier
Wellen mit 90° Phasenverschiebung.
Das Zeigerdiagramm ist in Abb. 220 wiedergegeben. Da die ursprünglichen Schwingungen eine Phasenverschiebung von 90° haben, handelt es sich um ein rechtwinkliges Dreieck. Die
Amplitude der resultierenden Schwingung ergibt sich aus dem Satz von Pythagoras, die gesuchte Phasenverschiebung aus der Definition des Tangens.
194
A res = 3 2 + 4 2 = 5
tan ϕ res = 4 , ϕ res = 53, 1 0
3
Man erkennt, daß die Lösung dieser Art von Aufgaben auf die Berechnung von Dreiecken
hinausläuft. Wenn das Dreieck nicht rechtwinklig ist, bietet sich der Kosinussatz an.
A 2res = A 21 + A 22 + 2A 1 A 2 cos (ϕ 2 − ϕ 1 )
iii. Drei Schwingungen gleicher Amplitude und gleicher gegenseitiger Phasendifferenz sollen
überlagert sich insgesamt auslöschen
.
Abb. 221: Drei gleiche Schwingungen mit jeweils 120° Phasenverschiebung addieren sich zu Null.
Man variiert den gegenseitigen Winkel im Zeigerdiagramm so lange, bis die Summe der drei
Vektoren verschwindet. Die Figur schließt sich dann zu einem Polygon (Abb. 221), in diesem
Fall zu einem gleichseitigen Dreieck mit drei gleichen Winkeln von 60°. Die Phasenverschiebung wird nach dem oben gesagten durch die Außenwinkel gegeben, in diesem Fall
ϕ 0 = 2π
3
Diese Situation liegt bei Wechselstrom vor. Wenn in den drei Phasen die gleichen Ströme fließen, ergeben sie an einem Knotenpunkt, an dem sie zusammenfließen, den Gesamtstrom 0.
4. Schwingung als komplexe Zahl
a) Komplexe Zahl
Abb. 222: Zeiger als komplexe Zahl
195
Der Zeiger, dessen Projektion eine Schwingung ergibt, kann statt in kartesischen Koordinaten
in der komplexen Zahlenebene dargestellt werden. Er repräsentiert dann eine komplexe Zahl.
Eine komplexe Zahl hat die Form
∼x = a + ib
wobei i die imaginäre Einheit, d.h. die Lösung der Gleichung x2 = -1 ist. Es gilt also i2 = -1.
Das Argument ϕ der komplexen Zahl ist der Winkel mit der reellen Achse (s. Abb. 222).
∼ ) = ∼x cos ϕ
a = Re(x
ist der Realteil von ∼x
∼ ) = ∼x sin ϕ
b = Im(x
ist der Imaginärteil von ∼x
∼
ϕ = artan b
a = arg (x )
ist das Argument von ∼x
∼x = a 2 + b 2 ist der Betrag von ∼x
∼x ∗ = a − ib ist die konjugiert komplexe Zahl zu ∼x
Der Betrag läßt sich auch schreiben
∼x = ∼x ⋅ ∼x ∗ ,
da
∼x ⋅ ∼x = (a + ib)(a − ib) = a 2 − (ib) 2
b) Algebraische Operationen mit komplexen Zahlen
Bei algebraischen Operationen behandelt man i wie eine normale Konstante. Dadurch, daß
man i2 durch -1 ersetzen darf, ist es bei Addition, Multiplikation und Division zweier komplexer Zahlen immer möglich, das Ergebnis in die Form a + ib zu bringen.
Addition:
∼x 1 + ∼x 2 = a 1 + ib 1 + a 2 + ib 2 = (a 1 + a 2 ) + i(b 1 + b 2 )
Multiplikation:
∼x 1 ⋅ ∼x = (a 1 + ib 1 )(a 2 + ib 2 ) = a 1 a 2 + i 2 b 1 b 2 + ib 1 a 2 + ib 2 a 1
= a 1 a 2 − b 1 b 2 + i(b 1 a 2 + a 2 b 1 )
196
Division ist Multiplikation mit dem Kehrwert. Es genügt daher zu zeigen, daß der Kehrwert
einer komplexen Zahl in die Form a + ib überführt werden kann.
1 =
a − ib = a − ib = a − i b
1
a + ib (a + ib) (a − ib) a 2 + b 2 a 2 + b 2 a 2 + b 2
c) Der Satz von Moivre
Funktionen von komplexen Zahlen erhält man, wenn man in die Taylorentwicklung einer reellen Funktion als unabhängige Variable eine komplexe Zahl einsetzt. Da jeder Term als Produkt komplexer Zahlen wieder eine komplexe Zahl ist, ist auch der resultierende Funktionswert eine komplexe Zahl. Der Satz von Moivre (manchmal auch Satz von Euler genannt) verknüpft die komplexe Funktion sin und cos mit der Exponentialfunktion. Um diese Verknüpfung zu verstehen, betrachten wir die Reihenentwicklungen dieser drei Funktionen nach einer
komplexen Variablen.
2
3
e x = 1 + x + x + x + ...
1! 2! 3!
2
3
4
e ix = 1 + i x − x − i x + x + ...
1! 2! 3! 4!
Entsprechend stellen wir die Reihen für sinx und cosx auf. Durch Vergleich dieser drei Reihen
ergibt sich der Satz von Moivre.
e ix = cos x + i sin x
Jede komplexe Zahl a + ib =|x|(cosϕ + isinϕ) kann also durch die oft bequemere Funktion
|x|eiϕ dargestellt werden.
Beispiel: Wie berechnet man i ?
Abb. 223: Wie man aus einer komplexen Zahl über den
Satz von Moivre die Wurzel zieht.
197
In der komplexen Zahlenebene (Abb. 223) erkennt man, daß i das Argument π/2 und den Betrag 1 hat. Das Argument wird mit dem Faktor i in den Exponenten der e - Funktion geschrieben, der Betrag vor die e - Funktion.
π
i = ei 2
Hier kann man die Wurzel leicht ziehen und dann mit dem Satz von Moivre
zurückverwandeln
e iπ/2 = e iπ/4 = cos π + i sin π = 1 2 + i 1 2
4
4 2
2
Beim Wurzelziehen aus einer komplexen Zahl wird also ihr Argument halbiert und aus ihrem
Betrag die Wurzel gezogen.
d) Anwendung der komplexen Zahlen auf Schwingungsprobleme
Hat man eine Schwingung
x = Acos(ωt + ϕ0)
so kann man ihr über den Satz von Moivre eine komplexe Zahl zuordnen, indem man
y = Asin(ωt + ϕ0)
als Imaginärteil hinzufügt. Liegt die ursprüngliche Schwingung in der Form x = Asin(ωt + ϕ0)
vor, so verwandelt man sie mit der Beziehung sinα = cos(α - π/2) in die Kosinusform. Die zugeordnete komplexe Zahl hat also die Form
∼x = A [cos (ωt + ϕ 0 ) + i sin (ϕt + ϕ 0 )]= Ae (ωt+ϕ 0 ) = Ae iϕ 0 e iωt
∼
A = Ae iϕ 0 ist die komplexe Amplitude. Sie enthält die Information über die Amplitude der
Schwingung
∼
A= A
198
(Dies folgt sofort aus A = A cos ϕ 0 + i sin ϕ 0 = A cos 2 ϕ 0 + sin 2 ϕ 0 ) und die Anfangsphase
∼
ϕ 0 = arg  A 
∼
A ist also in der komplexen Zahlenebene ein Zeiger, dessen Länge durch die Schwingungsamplitude und dessen Richtung gegenüber der reellen Achse durch die Anfangsphase
gegeben ist. Es gibt drei Möglichkeiten von einer komplexen Darstellung auf eine reelle
zurückzukommen.
Man addiert zu einer komplexen Schwingung die dazugehörige konjugiert komplexe
∼x + ∼x ∗ = (a + ib) + (a − ib) = 2Re(x∼ )
Man betrachtet den Realteil von ∼x als einzig interessierende Größe
Man nimmt ∼x als Amplitude und arg(x∼ ) als Anfangsphase.
Vorsicht! Terme, in denen das Produkt zweier Schwingungen auftaucht, etwa wie bei Energiebetrachtungen, dürfen nicht ohne weiteres komplex geschrieben werden. Am besten schreibt
man solche Terme reell, etwa
1 ∼x + ∼x ∗ ∼x + ∼x ∗ .
( 1
1 )( 2
2)
4
Man überlagert zwei Schwingungen, indem man ihre komplexen Amplituden addiert. Bei
gleicher Frequenz erhält man für die Summe der Schwingungen
∼ iωt
∼
∼x 1 = A
und ∼x 2 = A 2 e iωt
1e
∼ iωt ∼ iωt  ∼ ∼  iωt
∼x res = A
+ A2e = A1 + A2  e
1e
und damit für die Amplituden
∼
∼ ∼
A res = A 1 + A 2
Die Zeigeraddition von Schwingungen läßt sich also auch formal über die Darstellung von
Schwingungen mit komplexen Zahlen einsehen.
199
5. Die gedämpfte Schwingung
a) Die freie gedämpfte Schwingung
Abb. 224: Ein System, bei dem die Dämpfung proportional zur Geschwindigkeit ist.
An einer Masse greife zusätzlich zu einer rückstellenden Kraft F1 = - Dx eine Reibungskraft
an die ähnlich wie bei der Stokesschen Reibungskraft proportional zur Geschwindigkeit sein
••
möge: F 2 = −bv = − b x . Die Bewegungsgleichung lautet dann
••
•
m x = −Dx − b x
Und die Schwingungsgleichung daher
••
b x• + D x = 0
x +m
m
(11)
∼ ∼
Man löst sie mit dem Ansatz ∼x = Ae λt . Dann ist
∼
∼
∼x• = ∼
λe λt = λ∼x ,
•• ∼ ∼ ∼
∼
∼
x = λ 2 Ae λt = λ 2∼x
Einsetzen in Gleichung (11) ergibt die charakteristische Gleichung
∼ 2∼ b ∼∼ D ∼
λ x + m λx + m x = 0
∼2 b ∼ D
λ + mλ + m = 0
mit der Lösung
2
∼
λ 1,2 = − b ±  b  − D
m
2m
2m
∼
λ 1,2 = −δ ± δ 2 − ω 20
(12)
200
mit
δ= b
2m
Dämpfung
und
ω 20 = D
m
Frequenz bei verschwindender Dämpfung
Die allgemeine Lösung lautet dann
∼
∼
x = ∼c 1 e λ 1 t + ∼c 2 e λ 2 t
x kann als reelle Lösung aufgefaßt werden, ∼c 1 und ∼c 2 sind komplexe Konstanten, die aus den
Anfangsbedingungen bestimmt werden müssen. Die Lösungen unterscheiden sich grundsätzlich bei positivem und negativem Radikand in Gleichung (12).
Wenn δ
2
> ω02, d.h. im Falle großer Dämpfung, sind die λi reell. Es ergeben sich
Lösungen der Form e-Kt, wobei K reell ist. Es erfolgt keine Schwingung. Die
Auslenkung sinkt nach ihrem Maximum monoton auf 0.
Wenn δ 2 < ω02, d.h. im Falle kleiner Dämpfung, ist der Radikand negativ und es kann
ein i herausgezogen werden
δ 2 − ω 20 = (−1)  ω 20 − δ 2  = iω
Das System schwingt also mit der Frequenz ω, die gegeben ist durch
ω 2 = ω 20 − δ 2
Die allgemeine Lösung hat die Form
∼
x = Ae (−δ+iω)t + Be (−δ−iωt) = e −δt (Ae iωt + Be −iωt )
(13)
∼
∼
A und B sind durch die Anfangsbedingungen festgelegte Konstanten, die im allgemeinen
∼
∼
komplex sind A = a 1 + ib 1 B = a 2 + ib 2 . Setzt man diese in Gleichung (13) bei reellen An∼ ∼
fangsbedingungen ein, so zeigt sich, daß B = A ∗ . (Dies ist klar, da die linke Seite von
201
Gleichung (13) reell sein soll und e-iωt das konjugiert komplexe zu eiωt ist). Dadurch ergibt
sich eine reelle Gesamtlösung der Form
x = 2e
−δt
[a 1 (e iωt + e −ωt ) − ib 1 (e iωt − e −iωt )]= 2e −δt (a 1 cos ωt − b 1 sin ωt) = Ae −δt cos (ωt − ϕ)
Abb. 225: Die Amplitude der gedämpften Schwingung
nimmt exponentiell ab.
x0 = Ae-δt kann als eine zeitabhängige Amplitude aufgefaßt werden. Das System schwingt also
mit abnehmender Amplitude (Abb. 225) und einer Frequenz ω, die etwas kleiner als die der
ungedämpften Schwingung ist. Bei sehr kleiner Dämpfung, δ << ω0 ist diese Abweichung
wegen des quadratischen Zusammenhangs
2 

ω 2 = ω 20 − δ 2 = ω 20  1 − δ 2

ω 
schon bei nicht all zu kleinen δ/ω zu vernachlässigen. Das Amplitudenverhältnis im Abstand
der Periode ist
x 0 (t + T) e −δ(T+t)
= −δt = e −δT = const
x 0 (t)
e
δT = ln
x 0 (t)
= Λ nennt man das logarithmische Dekrement
x 0 (t + T)
ω 2π 2π
=
= ist die Güte des Schwingkreises.
δ Tδ Λ
Die zeitliche Abnahme der Amplitude ist proportional zur Amplitude selbst
dx 0
= −δx 0 (t)
dt
Dieses Verhalten ist typisch für Absorption, Zerfall oder Ähnliches.
b) Die erzwungene Schwingung
202
α) Die Schwingungsgleichung
Ein schwingungsfähiges System soll durch eine äußere periodische Kraft etwa wie in Abb.
226 angetrieben werden
Abb. 226: Die erzwungene Schwingung wird von außen periodisch angeregt.
F = F 0 e iωt
Nach einer Einschwingzeit stellt sich eine sinusförmige stationäre Schwingung mit der Frequenz ω ein. Diese Frequenz ist diejenige, mit der die äußere Kraft schwingt. Sie hat mit der
Frequenz der freien Schwingung des Systems ω0 nichts zu tun. Man interessiert sich in diesem
∼
Fall für die Frequenzabhängigkeit der Schwingungsamplitude A(ω) und die Phasenverschiebung zwischen äußerer Kraft und Schwingung des Systems
∼
∼
ϕ = arg (x∼ ) =atan  Im  A  /Re  A   .
••
•
m x + b x + Dx = F 0 e iωt
Bewegungsgleichung
••
b x• + D x = F 0 e iωt
x +m
m
m
Schwingungsgleichung
Mit den Abkürzungen δ = b/2m, ω02 = D/m und f = F0/m hat die Schwingungsgleichung die
Form
••
•
x + 2δ x + ω 20 x = fe iωt
(14)
β) Lösung für den eingeschwungenen Zustand
Um die Lösung für den eingeschwungenen Zustand zu finden, genügt es, eine spezielle Lösung anzugeben. Dafür macht man einen Ansatz, der aus der rechten Seite der Gleichung (und
eventuell ihren Ableitungen) zusammengesetzt ist.
203
•
x = Ae iωt
x = iωAe iω
••
x= − ω 2 Ae iωt
x und A sind hier komplexe Größen. Einsetzen in die Schwingungsgleichung ergibt
A  −ω 2 e iωt + 2δiωe iωt + ω 20 e iωt  = fe iωt
Hieraus folgt die komplexe Amplitude zu
A=
f
ω − ω 2 + 2δiω
2
(15)
Rational machen des Nenners ergibt
A=
f   ω 20 − ω 2  − 2iδω 


2
 ω 2 − ω 2  + (2δω) 2
 0

(16)
Durch Multiplikation von Gleichung (15) mit dem konjugiert Komplexen erhält man die
Amplitude
A2 =
f2
2
 ω 2 − ω 2  + (2δω) 2
 0

(17)
aus Gleichung (16) den gesuchten Phasenwinkel
−2δω
= 2δω
tan ϕ = ImA = 2
ReA ω − ω 2 ω 2 − ω 2
γ) Diskussion
Regt man mit der Frequenz an, mit der das System frei schwingt (ω = ω0), so ist der erste
Term im Nenner Null. Die Amplitude ist dann also in der Nähe des Maximums. Wenn ω sich
im Bereich des Maximums praktisch nicht ändert, liegt das Maximum sogar genau bei ω = ω0.
f
Diese Situation nennt man die Resonanz. In der Resonanz ist A =
. Die Amplitude ist
2δω
204
dann um so größer, je kleiner die Dämpfung ist. Dies kann in Brücken, die einer periodischen
Kraft ausgesetzt werden oder rotierenden Maschinenteilen zu Schädigungen führen. Die Phasenverschiebung ist Null für kleine Frequenzen, -π/2 bei Resonanz (die Schwingung hinkt um
π/2 hinter der Anregung) und π bei ω >> ω0 (Abb. 227 ). Für kleine Dämpfung δ << ω0 wird
die
Abb.
227:
Abhängigkeit
der
Amplitude und der Phasenverschiebung
der
erzwungenen
Schwingung von der Frequenz.
Breite der Resonanzkurve A(ω) klein, so daß alle interessierenden Amplituden in einem Frequenzbereich sehr dicht um die Resonanzfrequenz liegen: ω0 - ω = ∆ω << ω0. Dann ist
ω 0 + ω ∼ 2ω 0
ω 20 − ω 2 = (ω 0 − ω)(ω 0 + ω) ∼ 2∆ωω
Die Frequenzabhängigkeit der Amplitude (Gleichung (17) ) vereinfacht sich dann zu
A =
f2
2
4∆ω
Die Funktion f(∆ω) =
2
ω 20
+ 4δ
2
ω 20
=
f2
4ω 20 δ 2
1

1 +  ∆ω
δ 
2
1
ist eine Glockenkurve (Lorenztprofil, s. Abb. 228).
1 + (∆ω/δ) 2
Abb.228: Für kleine Dämpfungen geht die Resonanzkurve in ein Lorentzprofil über.
205
Die Halbwertsbreite, d.h. die Breite bei halber Zentralamplitude ist δ. Je mehr die Schwingung
gedämpft wird, desto breiter ist die Resonanzkurve. Spektrallinien, die aus gedämpften
Schwingungen stammen, besitzen Lorentzprofile. Um an Spektrallinien Präzisionsmessungen
der Wellenlänge durchführen zu können, etwa zur Festlegung des Urmeters, müssen Linien
kleiner Dämpfung ausgewählt werden. Das Himmelsblau stammt aus Streuung des Sonnenlichtes an Sauerstoffmolekülen, die ihre Resonanz im ultravioletten Spektralbereich haben,
d.h. bei hohen Frequenzen relativ zum sichtbaren Spektralbereich. Für (∆ω/δ) >>1 geht das
Abb. 229: Die Streuintensität am Sauerstoff nimmt im sichtberen
Spektralbereich mit der 4. Potenz der Frequenz ab. Daher erscheint der
Himmel blau. Dies ist eine Folge der erzwungenen Schwingung der O2
- Moleküle im Licht der Sonne..
Lorentzprofil mit 1/(∆ω)2 . Die Resonanzkurve steigt also zu hohen Frequenzen hin an. Daher
wird blaues Licht besser gestreut als rotes.
δ) Der Einschwingvorgang
Die allgemeine Lösung der Schwingungsgleichung (14) ist die Summe einer speziellen Lösung und der allgemeinen Lösung des homogenen Anteils der Schwingungsgleichung
••
•
x +2δ x +ω 20 x = 0
Die spezielle Lösung haben wir bisher betrachtet. Sie stellt eine stationäre Schwingung dar
und beschreibt daher den eingeschwungenen Zustand. Die allgemeine Lösung des homogenen
Anteils gibt den Einschwingvorgang wieder, d.h. die Anpassung zwischen den Anfangsbedingungen und der eingeschwungenen Lösung. Sie ist, wie man an der Differentialgleichung ersehen kann, eine gedämpfte Schwingung, die in der charakteristischen Zeit 1/2δ abklingt
(vergleiche Gleichung (11)). Das Einschwingen nimmt also umso mehr Zeit in Anspruch, je
weniger das System gedämpft ist. Im ungedämpften Fall würde die Einschwingzeit unendlich
lang sein und die Amplitude in der Resonanz unaufhörlich wachsen.
6. Überlagerung von Schwingungen ungleicher Frequenz oder ungleicher Richtung
a) Schwebungen
206
Zwei Schwingungen sollen fast gleiche Frequenz haben
ω1 ≈ ω2 = ω
ω 1 − ω 2 = ∆ω << ω
Die Addition der Schwingungen als komplexe Zahlen ist nach wie vor möglich, da hierbei
nicht auf den Sonderfall ω1 = ω2 eingeschränkt werden mußte. Im Zeigerbild ergibt sich als
Unterschied zu dem Fall gleicher Frequenzen daß die Zeiger, die die beiden betrachteten
Abb. 230: Jetzt laufen die Zeiger mit unterschiedlicher Frequenz um.
Schwingungen darstellen, mit leicht unterschiedlicher Drehzahl rotieren. Nach n Umdrehungen überholt der schnellere Zeiger den langsameren. Die resultierende Amplitude schwankt
zwischen A1 + A2 und |A1 - A2|. Dieses Phänomen nennt man Schwebung (englisch beat).
Abb. 231: Bei einer Schwebung ändert sich die
Amplitude mit der Differenzfrequenz der beiden
Wenn bei einer Umdrehung der zusätzlich vom schnelleren Zeiger zurückgelegte Winkel ∆ϕ
ist, benötigt man von einer Begegnung der Zeiger zur nächsten
n = 2π Umdrehungen.
∆ϕ
Da ω1 = 2π/T, ω2 =(2π + ∆ϕ)/T, gilt ∆ϕ/T = ∆ω und nachdem man T durch 2π/ω ersetzt,
∆ϕ/2π = ∆ω /ω und damit
n=
ω
∆ϕ
Für die Schwebungsperiode erhält man hiermit
207
T s = nT =
ω
T = 2π
∆ω
∆ω
Da ωs = 2π/Ts, ergibt sich
ω s = ∆ω
Die Frequenzdifferenz der Schwingungen ist genau die Schwebungsfrequenz. Dies ermöglicht
sehr genaue Messungen des Frequenzunterschiedes zweier Schwingungen. Der Nonius nutzt
diesen Vorteil bei Raumfrequenzen aus.
b) Überlagerung von Grundschwingungen und ihren Oberschwingungen
Die Schwingung mit einem ganzzahligen Vielfachen einer Grundfrequenz ω nennt man eine
Oberschwingung der ursprünglichen Schwingung. Also x = xnsin(nωt) (mit n = 1, 2, ..) sind
Oberschwingungen von x = x0sinωt. Durch Überlagerung einer Grundschwingung und ihrer
Abb. 232: Oben: Die ersten drei Glieder der Fourier
Entwicklung eins periodischen Rechtecks.
Unten: Die Summe der Einzelschwingungen.
Oberschwingungen entsteht eine nicht sinusförmige Schwingung mit der gleichen Periode wie
die Grundschwingung. Als Beispiel sind in Abb.232 die Glieder der Reihe
4  sin ωt + 1 sin 3ωt + 1 sin 5ωt + ... 
F(t) = π


3
5
und die sich ergebende Summe dargestellt. Im Grenzwert n → ∞ ergibt sich eine Rechtecksfunktion. Die Umkehr dieser Aussage ist der Satz von Fourier
Jede stückweise glatte Funktion mit der Periode T = 2π
ω , F(t) , läßt sich durch eine Reihe der
Form
∞
∞
=
=
F(t) = a 0 + Σ a n sin(nωt)+ Σ b n cos(nωt)
darstellen. Die Koeffiziente an und bn errechnen sich aus
208
T
T
T
a 0 = 1 ∫ F(t)dt, a n = 2 ∫ F(t)sin nωtdt, b n = 2 ∫ F(t)cos nωtdt
T0
T0
T0
Der Beweis erfolgt am besten über den Ansatz
F(t) =
∞
a n e inωt
Σ
=−∞
Man multipliziert rechts und links mit e-ikωt und integriert über eine Periode. Da für n ≠ k sich
in T periodische Funktionen ergeben, wird das Integral über T Null und auf der rechten Seite
bleibt nur der Term mit n = k übrig. Er ergibt
a n = 1 ∫ F(t)e −inωt dt
T
Durch Zusammenfassen der Terme mit positivem und negativem n ergibt sich die reelle
Darstellung.
Durch Frequenzanalyse kann man Aussagen über die an einer Schwingung beteiligten Prozesse gewinnen. Spektroskopie ist ein Beispiel von Frequenzanalyse in der Optik. In der Hochfrequenztechnik werden die Eigenschaften eines Übertragers oder Verstärkers im Frequenzraum angegeben. Ein realer Übertrager überträgt nicht alle Frequenzen gleichmäßig. Das Ausgangssignal hat daher eine andere Zusammensetzung als das Eingangssignal. Es erscheint verzerrt. Die Form des Ausganssignals kann ermittelt werden, indem man das Eingangssignal einer Fourieranalyse unterzieht, die einzelnen Amplituden mit dem Frequenzgang des Übertragers multipliziert und wieder überlagert. Ist der Zusammenhang zwischen Eingangssignal Ue
und Ausgangssignal Ua wie in Abb.233 nicht linear, so wird aus einem sinusförmigen Eingangssignal ein nicht sinusförmiges Ausgangssignal. Die Fourieranalyse muß daher Oberschwingungen zeigen. Diese können erwünscht sein, z.B. wenn man aus einer gegebenen
Schwingung eine mit höherer Frequenz erzeugen will (Frequenzverdopplung ist in der Lasertechnik ein übliches Verfahren), sie können in anderen Situationen wie Audioverstärker unerwünscht sein. Der Anteil der entstandenen Oberwellen bestimmt den Klirrfaktor.
209
Abb. 233: Eine nichtlineare Charakteristik zwischen Ausgang und Eingang führt zu Verzerrungen und damit zur Erzeugung von Oberfrequenzen.
k=
Σ A 2n
n=2
A1
c) Überlagerung von Schwingungen verschiedener Schwingungsrichtungen
Von den vielen Phänomenen, die durch die Überlagerung von Schwingungen entstehen, betrachten wir die Addition zweier Schwingungen entlang zweier senkrecht zueinander stehender Richtungen ex und ey im Raum (Abb. 234).
Abb. 234: Die Überlagerung von zwei Schwingungen, deren
Polarisationsrichtungen senkrecht aufeinander stehen..
x = x 0 cos ω 1 t
y = y 0 cos (ω 2 t + ∆ϕ)
Die Schwingungen sind dann vektoriell zu addieren. Der Summenvektor beschreibt eine Kurve in der x - y Ebene deren Parameterdarstellung durch die Zeitabhängigkeit seiner Koordinaten x(t), y(t) , gegeben ist, die hier die Auslenkungen der Einzelschwingungen sind. Die Kurve, die die Spitze des Summenvektors beschreibt, erhält man durch Elimination der Zeit.
Für den Fall, daß mω2 = nω1, d.h., daß die Frequenzen der Schwingungen sich wie ganze
Zahlen verhalten, entstehen die sogenannten Lissajous Figuren. Wir betrachten nur den Fall
gleicher Frequenzen.
210
x = x 0 cos ωt
y = y 0 cos (ωt + ∆ϕ)
i. Die Phasenverschiebung ist Null
Dann erhält man durch Division der beiden Gleichungen
x = y
x0 y0
y(x) ist eine Gerade. Die resultierende Schwingung ist linear polarisiert.
ii. ∆ϕ = −π/2
x = x0cosωt
y = y0sinωt
Durch Quadrieren und Summieren erhält man
2
2
 x  + y  =1
 x0 
 y0 
y(x) ist eine Ellipse, im Sonderfall x0 = y0 ein Kreis. Die Schwingung ist elliptisch oder zirkular polarisiert.
iii. ∆ϕ = π
y
x
x0 = − y0
Die Schwingung ist wieder linear polarisiert. Die Richtung der Geraden, auf der die Schwingung verläuft, hat in der x - y Ebene negative Neigung.
211
KAPITEL H
Spezielle Relativitätstheorie
1. Einleitung
a) Womit befaßt sich die Relativitätstheorie
Die spezielle Relativitätstheorie befaßt sich formal mit der Transformation von physikalischen
Gesetzen von einem Inertialsystem S in ein anderes S´, das sich gegenüber S gleichförmig geradlinig mit der Geschwindigkeit v bewegt. Ohne Verlust der Allgemeinheit legen wir die x Achse in die Bewegungsrichtung und wählen als Zeitnullpunkt die Zeit, bei der die Ursprünge
der beiden Koordinatensysteme zusammenfallen. Dann gilt in der klassischen Physik
Abb. 235: In der speziellen Relativitätstheorie geht es um
die Transformation aller möglicher physikalischer Größen
von einem Inertialsystem zu einem anderen, daß sich in x Richtung gegenüber dem ersten bewegt.
x´ = x - vt
t´ = t
y´ = y
z´ = z
Diese Transformationsgleichungen nennt man die Galilei Transformation. Da die Newtonsche
Bewegungsgleichung nur eine Aussage über die Beschleunigung macht, und die Galilei Transformation Beschleunigungen nicht ändert, gelten die Newtonschen Axiome in S und S´ und
man kann mit mechanischen Experimenten nicht unterscheiden, ob ein System in Ruhe ist
oder nicht. In der Relativitätstheorie fordert man darüber hinaus, daß man prinzipiell nicht entscheiden kann, ob man sich in einem ruhenden oder einem bewegten System befindet, also
insbesondere nicht durch Experimente mit Licht. Führt man diesen Gedanken konsequent
durch, so stellt man fest, daß die Galilei Transformation ausgebessert werden muß. Man ändert sie so ab, daß sie für v << c erhalten bleibt. Bei großen Geschwindigkeiten ergeben sich
substantielle Änderungen. Insbesondere wird sich zeigen, daß gleich gebaute Uhren nicht
212
gleich schnell gehen, d.h. t ≠ t´, und daß ebenso das Ergebnis von Längen - oder Massenmessungen von der Relativgeschwindigkeit von S und S´ abhängt.
Die Relativitätstheorie führt zu einem Raum - Zeit Begriff, der dem "gesunden Menschenverstand" zu widersprechen scheint. Ebenso werden gegenüber der klassischen Physik die Begriffe Masse und Energie revolutioniert. Die Relativitätstheorie hat deswegen über die Physik hinaus Bedeutung erlangt, da sie zu einer Erweiterung des Denkens über Raum, Zeit und Energie
führt.
b) Der Äther
Im Altertum bis ins 18. Jahrhundert benutzte man den Ätherbegriff, um den leeren Raum anzufüllen, wie z.B. bei Aristoteles, und um sich die Kraftübertragung zwischen entfernten Körpern mechanisch vorstellen zu können. Bei Aristoteles überträgt der Äther die Kraft zwischen
den Himmelssphären. Bei Descartes besteht der Äther aus verschiedenen Teilchen, für die verschiedenen Kraftarten. Newton macht keine detaillierte Theorie des Äthers, benötigt den
Äther auch nicht für die Lichtausbreitung, da er die Korpuskulartheorie des Lichtes vertritt,
glaubt aber an die Existenz des Äthers, auf den man den absoluten Raum beziehen kann. Er
meint, wenn der Äther nur 700 000 mal dünner und elastischer als Luft ist, würde die Störung
der Planetenbewegung durch ihn in 10 000 Jahren nicht bemerkbar sein.
Seit der Entdeckung der Wellennatur des Lichtes durch Thomas Young (1801) benötigte man
den Äther für den Ausbreitungsmechanismus dieser Wellen. Faraday vermutete in den Spannungszuständen des Äthers die Ursache für elektromagnetische Kräfte. James Clark Maxwell
entwickelte mit einem mechanischen Modell vom Äther das theoretische Gebäude des Elektromagnetismus, das interessanterweise noch heute gültig ist und die erste mit der Relativitätstheorie kompatible Theorie darstellt. Als Heinrich Hertz die von Maxwell vorhergesagten
elektromagnetische Wellen experimentell herstellte, schien klar, daß der Äther das Übertragungsmedium für elektromagnetische Kräfte und damit für das Licht ist. Am Ende des 19.
Jahrhunderts war der Äther ein zentraler Begriff in der Physik und die Bestimmung der Eigenschaften des Äthers ein wichtiges Anliegen.
c) Versuche zur Bewegung der Erde durch den Äther
α) Aberration des Lichtes
James Bradley entdeckte 1725, daß sich die Position von Sternen jahreszeitlich ändert. Die
scheinbare Position beschreibt eine Ellipsenbahn, die ein Bild der Projektion der Erdbahn in
der Beobachtungsrichtung ist. Dieser Effekt läßt sich mit der vektoriellen
213
Abb.236: Durch die Aberration des Lichtes beschreiben Fixsterne am Himmel Ellipsen, die eine Projektion
der Erdbahn um die Sonne darstellen.
Geschwindigkeitsaddition der Geschwindigkeit der Erde auf ihrer Bahn und der Lichtgeschwindigkeit erklären, wenn der Äther nicht mit der Erde mitbewegt wird (Abb. 236).
β) Versuche von Fizeau
Fizeau maß die Lichtgeschwindigkeit in strömenden Medien und fand einen Mitführkoeffizienten. Es ergab sich in einem strömenden Medium für die Geschwindigkeit cmit in
Bewegungsrichtung
c mit = nc + v  1 − 12 


(n ist der Brechungsindex des Mediums, v seine Geschwindigkeit und c die Lichtgeschwindigkeit). Da der Brechungsindex der Luft sehr nahe an 1 liegt, ergibt sich praktisch keine Mitführung des Äthers durch die Lufthülle der Erde. Soweit stimmen die Ergebnisse. Allerdings
schlugen alle Versuche, die Relativbewegung der Erde zum Äther zu messen, fehl.
γ) Die Versuche von Trouton und Nobel
Trouton und Nobel versuchten die Kräfte des Äthers auf einen geladenen Kondensator
festzustellen.
δ) Versuche von Michelson und Morley
Abb. 237: Das Michelson Interferometer
Am bekanntesten ist der Versuch von Michelson und Morley 1881 Berlin, 1886 USA. Michelson baute ein Interferometer auf, wie es im Prinzip in Abb. 237 dargestellt ist. Ein Lichtstrahl
214
wird durch einen teildurchlässigen Spiegel so aufgeteilt, daß beide Teilstrahlen senkrecht zueinander stehende Wege durchlaufen. Nach Überlagerung beider Strahlen kann man die Phasenverschiebung feststellen. Wenn einmal der Strahl (1) parallel zur Geschwindigkeit der Erdrotation dann durch Drehen der ganzen Anordnung senkrecht dazu ausgerichtet wird, ergibt
sich eine unterschiedliche Beeinflussung durch den Ätherwind und damit eine unterschiedliche Phasendifferenz.
Bei Bewegung parallel zu v sollte auf dem Hinweg c´ = c + v, auf dem Rückweg c´ = c - v
gelten. Hierin ist c die Geschwindigkeit des Lichtes im ruhenden Äther, c´ im bewegten System. Die für Hin - und Rücklauf benötigte Zeit beträgt dann
1
D
2Dc
2D
t1 = c D
−v + c+v = 2− 2 = c − 2
2
Bei einer Bewegung der Apparatur senkrecht zur Ausbreitungsrichtung des Lichtes sollte nach
Abb. 238 auf Hin - und Rückweg gelten:
c 2 = c 2 − v 2 und t 2 =
1
2D
= 2D
c
1 − v 2 /c 2
c2 − v2
Abb.238: Dieses Dreieck würde man in der klassischen
Physik bei der Geschwindigkeitsaddition zeichnen.
Die Zeitdifferenz t1 - t2 sollte bei Drehung der Apparatur um 90° das Vorzeichen ändern. Das
Michelson - Morley Experiment zeigte keine Änderung des Interferenzmusters bei Drehung
der Apparatur. Daraus ließ sich ableiten, daß die Relativbewegung gegenüber dem Äther kleiner als 1 km/s sein mußte, obgleich die Erddrehung alleine zu einer Geschwindigkeit v = 30
km/s führt. Das Michelson Experiment wurde seit dem in unterschiedlichen Varianten wiederholt, z.B. mit γ - Quanten, d.h. elektromagnetischer Strahlung von 1022 Hertz, mit bewegten
Quellen, Sternen als Lichtquellen, mit größerer Genauigkeit. Heute könnte man eine Geschwindigkeit von 3 cm/s nachweisen. Keins der Experimente zeigt eine Relativbewegung der
Apparatur zum Äther.
Es gab verschiedene Erklärungsversuche, z.B. daß sich alle Körper in der Geschwindigkeitsrichtung relativ zum Äther zusammenziehen. Diesen Effekt nennt man die Lorentzkontraktion.
215
Man erhält dann allerdings Probleme bei Rotationsbewegungen. Die eleganteste Lösung ist
die von Albert Einstein, dargelegt in seinem 1905 erschienenen Artikel "Zur Elektrodynamik
bewegter Körper". Einstein folgerte aus dem negativen Ausgang des Michelson - Morley Experimentes, daß es keine Relativbewegung zum Äther gibt, da es keinen Äther gibt.
2. Aufbau der Relativitätstheorie
a) Die Grundpostulate
α) Relativitätsprinzip
Die Naturgesetze nehmen in allen Inertialsystemen die gleiche Form an
β) Prinzip der Konstanz der Lichtgeschwindigkeit
Die Lichtgeschwindigkeit im Vakuum hat in jedem Inertialsystem den Wert c = 3·108m/s.
Hieraus ergeben sich sofort einschneidende Folgerungen.
b) Direkte Folgerungen der Grundpostulate
α) Die Gleichzeitigkeit ist relativ
Zwei Ereignisse, die in einem Inertialsystem gleichzeitig erfolgen, sind in einem andern nicht
unbedingt gleichzeitig.
Wir wollen uns nicht mehr darauf verlassen, daß es Uhren gibt, die in verschiedenen Inertialsystemen gleich laufen. Wir müssen also eine Meßanordnung angeben, die es gestattet, gleichzeitige Ereignisse zu erkennen. Für die Entwicklung der Relativitätstheorie sind solche Meßanordnungen charakteristisch. Auch zur Messung von Längen und Zeiten werden bestimmte
Meßverfahren ersonnen. Gedanklich besonders einfach sind solche, die sich auf die Ausbreitung von Licht stützen, da postuliert wird, daß sich dieses in allen Inertialsystemen mit gleicher Geschwindigkeit ausbreitet. Wir nennen zwei Ereignisse gleichzeitig, wenn sie von einem Lichtblitz ausgelöst werden, der von einem Punkt ausgeht, der genau in der Mitte zwischen beiden Ereignissen liegt, bzw. wenn von ihnen ausgehende Lichtsignale gleichzeitig in
einem Punkt in der Mitte ankommen. Für die Gleichzeitigkeit zweier Ereignisse die am gleichen räumlichen Punkt stattfinden, bleibt die alte Definition.
Orte und Zeiten werden in einem Inertialsystem mit den üblichen Methoden d.h. mit Maßstäben und Uhren gemessen. Nachdem man diese abgelesen hat, werden die Werte unter Berücksichtigung der Laufzeit der Nachricht an eine Kommandozentrale übergeben.
Beispiel: Die Begegnung zweier Galaxien.
Im oberen Teil der Abb. 239 ist die Situation aus der Sicht von Galaxie B, im unteren Teil aus
Sicht von Galaxie A dargestellt. Wenn die Mitten übereinander liegen, wird in der Mitte ein
216
Abb. 239: Was von einem System aus als gleichzeitig erscheint, kann von einem dazu bewegten System durchaus
als nacheinander beurteilt werden.
Lichtblitz gezündet. Aus der Sicht der Galaxie B kommt der Blitz zuerst am hinteren Ende
von A an, dann gleichzeitig an beiden Enden der Galaxie B und zuletzt am vorderen Ende von
A. Aus Sicht der Galaxie A kommt der Blitz zuerst am Ende von B an, dann an beiden Enden
von A und am Schluß an der Spitze von B. Was in einer Galaxis als gleichzeitig interpretiert
wird, erfolgt also in der anderen nacheinander.
β) Gleichgebaute Uhren gehen in verschiedenen Inertialsystemen nicht gleich schnell.
Zum Beweis konstruieren wir eine Lichtuhr, in der ein Lichtstrahl zwischen zwei Spiegeln mit
dem Abstand l hin und her reflektiert wird und die Perioden gezählt werden. In einem ruhenden Bezugssystem S seien zwei synchronisierte Uhren A und B. In einem bewegten System S´
ist eine gleich gebaute Uhr C, die die gleiche Zeit anzeigt, wie A, wenn A und C am gleichen
Ort sind (Abb. 240).
Abb.240: Unten ist ein ruhendes System S mit zwei synchronisierten Uhren, die nacheinander abgelesen werden. Oben ist ein bewegtes System S´, mit einer gleich gebauten Uhr. Diese wird bei
der Begegnung mit A auf 0 gestellt und bei der Begegnung mit B abgelesen. Sie zeigt eine andere
217
Wenn das Licht in der Uhr C einmal hin und her gelaufen ist, zeigt C die Zeit t´ = 2l/c an.
Von S aus gesehen dauert das Hin- und Herlaufen länger, da der Weg längs der Hypothenuse
zurückgelegt wird. Die angezeigte Zeit ist t = 2H/c. H läßt sich aus dem rechtwinkligen Dreieck ausrechnen.
2 (vt/2) 2 + l 2
t=
c
Quadrieren und Ausnutzen der Bedinging t´ = 2l/c, also l = ct´/2 ergibt
2
2
 tc  −  tv  = l 2 =  ct / 
2
2
2 
t=t
2
1
1 − (v/c) 2
Beispiel:
3
c . Es folgt 1 − (v/c) 2 = 1/2 und t = 2t´.
2
Die Uhren im bewegten System scheinen also langsamer zu laufen. Von Uhr C aus gesehen
Es sei v =
wird mit zwei Uhren in S verglichen, über deren Gleichzeitigkeit keine Aussage gemacht werden kann. Vergleicht man zwei Uhren in S´ auf gleiche Weise mit A, ergibt sich die Aussage
t´ = 2t. Diese Aussagen ist auch für anders gebaute Uhren korrekt. Gäbe es Uhren, die bei dem
Vergleich zu einem anderen Ergebnis führen würden, könnte man unter den verschiedenen
Inertialsystemen eins auswählen, nämlich das, mit dem kleinsten Gangunterschied zwischen
den Uhren. Dieses wäre ein Verstoß gegen das Relativitätsprinzip, das ja die Auszeichnung eines der Inertialsysteme verbietet. Man kann also auch biologische Uhren verwenden. Bei dem
obigen Beispiel würde das heißen, daß z.B. der Mensch C wäre mit der dargestellten Methode
gemessen nur halb so alt wie Mensch B.
γ) Längen werden unterschiedlich gemessen
Wie beim Zeitvergleich ist der Längenvergleich senkrecht zu v unkritisch. Aber parallel zu v
hängt das Ergebnis einer Längenmessung eines bewegten Körpers von der Definition der
Gleichzeitigkeit ab. Will man von S aus die Länge eines bewegten Objektes messen, so wird
man gleichzeitig zwei Markierungen anbringen. Von S´ aus gesehen erfolgen die
218
Markierungen nicht gleichzeitig, so daß man die Längenmessung gegenüber der eigenen als
falsch beurteilt.
c) Lorentztransformation
α) Herleitung der Transformationsformeln
Zur formalen Herleitung der Transformationsgleichungen, die x, t in x´, t´ transformieren, machen wir folgende Voraussetzungen:
Eine in S geradförmige, gleichförmige Bewegung eines Massenpunktes ist auch von S´
aus gesehen gleichförmig, geradlinig. Diese Forderung folgt aus dem Relativitätsprinzip.
Wenn nämlich von S´ aus die Bewegung nicht gleichförmig, geradlinig wäre, wäre S
vor S´ ausgezeichnet
Die Lichtgeschwindigkeit ist in S und S´ gleich groß.
Für v → 0 ergibt sich die Galilei Transformation.
Aus der ersten Forderung folgt, daß die Transformationsgleichungen linear sein müssen. Setzt
man außerdem den Zeitnullpunkt so fest, daß bei t = 0 und x = 0 auch x´ = 0 und t´ = 0, so
bleibt die Form
x´ = Ax + Bt
t´ = Cx + Dt
(1)
Der Ursprung von S´soll sich in S mit der Geschwindigkeit v bewegen. Wegen der dritten
Forderung muß sich dann der Ursprung von S in S´ mit -v bewegen.
Aus x´ = 0 folgt dann Adx + Bdt = 0 und aus dx/dt = v folgt dann v = − B
A
Aus x = 0 folgt x´ = Bt und t´ = Dt und aus dx´/dt´ = -v folgt dann v = − B
D
Aus dieser Beziehung liest man ab
D=A
B = -vA
Berücksichtigt man dies in Gleichung (1), erhält man
x´ = Ax - vAt
219
t´ = Cx + At
(2)
Wegen der Konstanz der Lichtgeschwindigkeit muß gelten
x´2 = (ct´)2
(3)
x2 = (ct)2
(4)
Gleichung (2) wird in Gleichung (3) eingesetzt:
(Ax - vAt)2 = (Cx + At)2c2
Die Klammern werden ausmultipliziert
A2x2 - 2A2xvt + v2A2t2= c2C2x2 + 2c2CAxt + c2A2t2
und nach Potenzen von x bzw. t geordnet
x2(A2 - c2C2) - 2xtA(Av + c2C) + t2A2(v2 - c2) = 0
Vergleicht man die Koeffizienten mit denen von Gleichung (4) in der Form x2 - (ct)2 = 0, so
erhält man
A2 - c2C2 = 1
vA + c2C = 0
(v2 - c2)A2 = -c2
Aus der letzten Gleichung folgt sofort
A=
1
1 − v 2 /c 2
Hiermit läßt sich aus der zweiten Gleichung C berechnen
220
C = − v2 A =
c
−v/c 2
1 − v 2 /c 2
In Gleichung (2) eingesetzt führt zur Lorentz Transformation
x/ =
x − vt
1 − v 2 /c 2
t/ =
t − (v/c 2 )x
(5)
1 − v/c 2
Zur Symmetrisierung setzt man ct = τ und ct´ = τ´. τ ist also die Zeit in Einheiten der Laufzeit
des Lichtes über die Distanz von 1m gemessen. Die Lorentz Transformation hat dann die
Form
x/ =
x − vc (tc)
1 − v 2 /c 2
t/c =
(tc) − vc x
1 − v 2 /c 2
Mit den Abkürzungen β = v/c und γ =
1
ergibt sich die übersichtliche Form der
1 − β2
Lorentztransformation
x / = γ(x − βτ),
τ / = γ(τ − βx)
β) Diskussion der Lorentz Transformation
i. Übergang zur Galilei Transformation
Abb. 241: Die Funktion γ(β) hat einen relativ scharfen
Knick bei β = 1.
Entwickelt man die Transformationsformeln in einer Taylorentwicklung nach β bis zum linearen Glied, d.h. so, daß β so klein sein soll, daß alle Terme mit β2 = (v/c)2 vernachlässigt
221
werden können, während solche mit v/c mitgenommen werden, so geht γ gegen 1. Für βτ wird
wieder vt geschrieben. Die Transformation für x lautet dann
x´ = x -vt
vt ist von der Größenordnung x und muß deshalb berücksichtigt werden. Die Transformation
der Zeit lautet also
t´ = t - (v/c2)x = t - (v2/c2)(x/v).
Wegen der gleichen Größenordnung von x und vt fällt hier der zweite Term weg. Die Lorentz
Transformation geht also für kleine Relativgeschwindigkeiten v in die Galilei Transformation
über. Wie Abb. 241 zeigt, bleibt γ in einem weiten Bereich der Geschwindigkeiten nahe 1, so
daß die Abweichung von der Galileitransformation erst in der Nähe der Lichtgeschwindigkeit
zum Tragen kommt.
ii. Die Umkehrtransformation
Durch Auflösen der Lorentz Transformation nach x und τ erhält man mit 1 - β2 = 1/γ2
x / = x − βτ
γ
τ / = τ − βx
γ
Durch Multiplikation der ersten Gleichung mit β erhält man
βx / τ /
τ
2
γ + γ = τ( 1 − β ) = γ 2
→
τ = γ(τ / + βx / )
Durch Multiplikation der Zweiten Gleichung mit β und Addition mit der ersten Gleichung
x/ + β τ/ = x 1 − β2
(
)
γ γ
→
x = γ(x / + βτ / )
Wie zu erwarten, ergeben sich die Transformationsgleichungen für x und τ aus den Gleichungen für x´ und τ´, indem man v durch -v ersetzt.
iii. Die Zeitdilatation
Eine Uhr, die in x´ = 0 ruht, zeigt die Zeit τ´. Wie groß ist dann τ?
222
Aus der Lorentztransformation mit x´ = 0 folgt τ´ = γ(τ - βx) und x = βτ. Durch Eliminieren
von x erhält man
τ´ = γ(τ − β2τ) = γ(1 − β2)τ = τ/γ
τ / = τγ
(6)
Da γ > 1, zeigt die Uhr in S´ weniger an als die in S. Eine Uhr, die in x = 0 ruht, zeigt die Zeit
τ. Wie groß ist τ´? Aus der Lorentz Transformation mit x = 0 folgt
τ / = γτ .
Die Uhren im jeweils anderen System zeigen jeweils eine kleinere Zeit an. Dies ist nicht paradox, da der Zeitvergleich einer Uhr in S mit mehreren Uhren in S´gemacht wird, über deren
Gleichzeitigkeit man nichts weiß und umgekehrt. Beim Zwillingsparadoxon vergleicht man
nur zwei Uhren. dafür muß aber die eine von ihnen zwischendurch beschleunigt werden.
iv. Die Längenkontraktion
Ein Maßstab, der so gelegt ist, daß die Enden bei x1´ = 0 und x2´ = L in S´ ruhen, wird von S
aus zur Zeit τ = 0 gemessen. Dann ergibt die Lorentz Transformation
L / = γL
(7)
Der Maßstab erscheint von S aus in Bewegungsrichtung kontrahiert.
v. Die Geschwindigkeitstransformation
•
Ein Körper habe in S die Geschwindigkeit u = x . Welche Geschwindigkeit mißt man in S´?
Durch Differentiation der Lorentz Formeln nach der Zeit erhält man
dx´ = γ(dx - βdτ) = γ(ux - β)dτ
dτ´ = γ(dτ − βdx) = γ(1 - βux)dτ
und damit
/
ux − β
u /x = dx / =
1 − βu x
dτ
223
Da dy´ = dy und dz´ = dz, ergeben die anderen Komponenten
u /y =
dy /
1
= uy
/
γ(1 − βu x )
dτ
/
1
u /z = dz / = u z
γ(1 − βu x )
dτ
Um die Zeit in die Sekundenskala zurück zu transformieren, beachtet man, daß dτ = cdt.
u = dx = dx = vc
dτ cdt
v /x =
vx − v
v⋅v
1 − 2x
v /y = v y
v /z
= vz
1 − β2
1−
v⋅v x
(8)
2
1 − β2
1−
v⋅v x
2
v . Setzt man beispielsweise v/ = c, so
Nach vx aufgelöst ergibt die erste Gleichung v x = c +v⋅v
x
/
1 + 2x
folgt v x = c + vv = c . Klassisch würde man in diesem Beispiel vx= v + c erwarten. Relativi1+
stisch ist die resultierende Geschwindigkeit kleiner. Durch die Regeln der Geschwindigkeitstransformation bleibt die resultierende Geschwindigkeit unter c. Hier muß eine Warnung
angebracht werden! Rechnerisch können Geschwindigkeiten größer als c vorkommen, z.B.
wenn in einem System zwei Lichtstrahlen gegeneinander laufen, geht die Änderung des Abstandes der Strahlenfronten mit 2c. Ebenso kann der Schnittpunkt zweier leicht geneigter Geraden, die fast senkrecht zur Geschwindigkeit verlaufen eine beliebig hohe Geschwindigkeit
haben (s. Abb. 242). Diese ist allerdings physikalisch nicht relevant. Insbesondere kann man
mit ihr keine Signale übertragen. Die maximale Geschwindigkeit eines Teilchens ist die des
Lichtes im Vakuum c0. In Medien, in denen die Lichtgeschwindigkeit kleiner als die des Vakuums ist, können sich Körper mit einer größeren Geschwindigkeit v bewegen als die des
Lichtes in diesem Medium c < v < c0.
224
Abb. 242: Es gibt auch in der Relativitätstheorie Geschwindigkeiten, die größer als die Lichtgeschwindigkeit sind.
vi. Transformation des Impulses
Um die Transformation des Impulses senkrecht zur Relativbewegung der Systeme S und S´ zu
ermitteln, wird gefordert, daß bei einem Stoß von jedem System aus die Impulserhaltung gelten soll. Es wird ein zentraler Stoß von zwei gleichen Teilchen im Schwerpunktsystem betrachtet (s. Abb. 243).
Abb. 243: Die Impulserhaltung soll von jedem System aus
gelten.
Die Massen m und die Geschwindigkeiten u beider Teilchen sind vor und nach dem Stoß
gleich groß. Von einem System S aus betrachtet, das sich mit v = ux parallel zur x - Achse bewegt, und einem S´, daß sich mit v = -ux bewegt, müssen die Figuren wegen der Gleichheit
der beiden Teilchen völlig symmetrisch aussehen. Daher ist die senkrechte Komponente des
Impulses p2⊥ die Größe, die man erhält, wenn man p1 von dem System S nach S´ transformiert
p2⊥´ = p1⊥
Abb. 244: Der gleiche Stoß wie in Abb. 243 von verschiedenen Inertialsystemen aus gesehen.
Da gefordert wurde, daß bei einem Stoß weiterhin p1⊥ = p2⊥ gelten soll, erhält man aus
p2⊥´ = p1⊥ und p1⊥ = p2⊥
225
p1⊥ = p1⊥´.
Daher ändert sich bei Lorentztransformation die senkrecht zu v stehende Komponente des Impulses nicht!
p⊥ = p⊥´
vii. Transformation der Masse
Die Masse definiert man über
p = mv
Da wir zunächst nur die Transformation von p⊥ kennen, betrachten wir ein Teilchen, das sich
in S senkrecht zur Geschwindigkeitsrichtung der beiden Systeme zueinander bewegt. Um einfache Verhältnisse zu erhalten, soll vy sehr klein sein, so daß von S aus gesehen noch keine relativistischen Effekte berücksichtigt werden müssen. Für ein Teilchen, das sich entlang der y Achse bewegt, ist
p⊥ = m0uy
Von S´ aus gesehen
p⊥´ = mvuy´
Wegen der Transformation von uy mit ux = 0 erhält man
uy´ = uy/γ
und wegen
p⊥ = p⊥´
mv uy/γ = m0uy
226
mv =
m v = γm 0
m0
1−
(9)
v 2
(c)
m0 ist die Ruhemasse, mv die dynamische Masse. mv wächst bei steigender Geschwindigkeit
gegen unendlich, wenn die Geschwindigkeit sich der Lichtgeschwindigkeit nähert. Man kann
also keinen Körper mit konstanter Kraft auf eine höhere Geschwindigkeit als die Lichtgeschwindigkeit beschleunigen. c ist der asymptotische Grenzwert. Bei der Konstruktion von
Teilchenbeschleunigern muß dieses Anwachsen der Masse berücksichtigt werden.
Mit der Transformationsformel für m und u lassen sich die Transformationsformeln für alle
übrigen Komponenten von p ableiten. Ebenso die Transformationsformeln für die Kraft:
•
(10)
F= p
viii. Die kinetische Energie
Die kinetische Energie errechnet man wie in der klassischen Mechanik aus der Arbeit, die
man verrichtet, um ein Teilchen von 0 auf v zu beschleunigen.
mu
E kin = ∫ Fds = ∫ d (mu)ds = ∫ d(mu) ds = ∫ ud(mu)
dt
dt
Durch partielle Integration
∫ udV = [uV] − ∫ Vdu
mit
V = mu und dV = d(mu)
v
∫0 ud(mu) =
v
v
[mu 2 ] 0 −
∫0 mudu =
m0v2
1 − (v/c) 2
v
−∫
0
m 0 udu
1 − (u/c) 2
Das Integral wird gelöst mit der Substitution ξ = 1 - (u/c)2, wobei dann dξ = − 22 udu .
v
∫0
udu
1 − (u/c) 2
2
= −c
2
v
∫0
dξ
v
= −c 2  1 − u 2 /c 2 

0
ξ
227
Dadurch wird die kinetische Energie
m0v2
E kin =
+ m 0 c 2 1 − v 2 /c 2 − m 0 c 2
1 − v /c
Der zweite Term wird mit der Wurzel erweitert
E kin =
2
2
m0v2 + m0c2 − m0v2
1 − v /c
2
2
− m 0 c 2 = (m − m 0 )c 2
(11)
E kin = (m − m 0 )c 2
Der Gewinn an kinetischer Energie entspricht dem Gewinn an Masse. Für kleine Geschwindigkeiten kann der Wurzelausdruck im Nenner entwickelt werden


1
− 1  ≈ m 0 c 2  1 − 1 β 2 − 1  = 1 m 0 v 2
E kin = m 0 c 
 1 − β2

2
2


2
Man erhält also den klassischen Ausdruck für die kinetische Energie zurück. Der relativistische Ausdruck für die kinetische Energie (Gleichung 11) legt nahe, daß die Ruhemasse auch
in andere Energieformen umgewandelt werden kann. Man bezeichnet
E = E kin + m 0 c 2 =
m0c2
1 − v /c
2
2
= mc 2
(12)
die Gesamtenergie des Körpers. Oft ist es bequemer die Gesamtenergie in Abhängigkeit von
m0 und p auszudrücken statt von m0 und v. Aus
p = mv
E = mc2
folgt v = (p/E) c2. Eingesetzt in Gleichung (12) in der Form E2(1 - v2/c2) = (m0c2)2 ergibt
E 2 − p 2 c 2 = (m 0 c 2 )
d) Minkowski Diagramme
2
(13)
228
α) Was sind Minkowski Diagramme ?
Ein Minkowski Diagramm stellt den x/t Raum des Systems S in rechtwinkligen Koordinaten
dar. Das Weg - Zeit Gesetz des Ursprungs von S´, x´ = 0, wird als Achse t´eingezeichnet. Da
x´ = γ(x − βτ)
τ´ = γ(τ − βx)
erhält man für x´ = 0 die Gerade τ = (1/β)x. Die Gerade τ´ = 0 wird als Achse x´ eingezeichnet. aus τ´ = 0 folgt τ = βx. Die x´ und τ´ Achsen sind symmetrisch zur Winkelhalbierenden
von τ und x. τ´ und x´ spannen ein schiefwinkliges Koordinatensystem auf, in dem man die
Lage eines Ereignisses (x´, τ´) ablesen kann, indem man durch den Punkt (x´, τ´) Parallele zu
den Achsen τ´ und x´ zeichnet und die Achsenabschnitte abliest (Abb. 246).
Abb. 245: Zwei gegeneinander bewegte Koordinatensysteme
im Minkowski Raum dargestellt.
Abb. 246: Wie man in einem schiefwinkligen Koordinatensystem die Koordinaten abliest.
Gleichzeitig kann man die zu x´, τ´ gehörenden Werte x, τ im Koordinatensystem x/t wie üblich ablesen. Um dies quantitativ möglich zu machen, müssen die Einheitsabschnitte auf den
Achsen angegeben werden. x = 1, τ = 0 und x = 0, τ = 1 können direkt eingetragen werden
(Abb. 247). Der Einheitsabschnitt auf der x´ - Achse ist gegeben durch
x´= 1, τ´ = 0
γ(x − βτ) = 1
γ(τ − βx) = 0
229
Aus der letzten Gleichung folgt τ = βx. Dies in die vorletzte eingesetzt γ(x − β2x) = 1, und mit
der Definition von γ: x = γ > 1. Entsprechend erhält man für den Einheitsabschnitt auf der τ´ Achse
τ´= 1, x´= 0
γ(x − βτ) = 0
γ(τ − βx) = 1 = γ(1 − β2)τ
und damit τ = γ > 1.
β) Zeitdilatation und Längenkontraktion im Minkowski Diagramm
Abb. 248: Zeitdilatation am Minkowski Diagramm
abgelesen.
Wenn τ´ = 1 und x´ = 0 folgt nach Abb. 248 τ > 1. Abb. 249 zeigt, wie sich die Längenkontraktion im Minkowski Diagramm darstellt. Ein Einheitsstab, der in S´ ruht, wird in S ausgemessen. Man hat also zwei in S gleichzeitige Ereignisse, sagen wir bei τ = 0. In S´ hatte man
durch gleichzeitige Messung der Enden, etwa zur Zeit τ´ = 0 die Länge L´ gemessen. An der
Konstruktion von Abb. 249 erkennt man, daß die in S gemessene Länge kürzer ausfällt.
Abb. 249: Längenkontraktion abgelesen am Minkowski
Diagramm.
γ) Gegenwart, Vergangenheit und Zukunft
230
Abb. 250: Die zeitliche Reihenfolge der Ereignisse A
und C (gekennzeichnet durch die dicken Punkte) kehrt
sich beim Übergang vom System S nach S´ um.
Abb. 251: Wieso die Kausalität verletzt würde, wenn man Signale mit Überlichtgeschwindigkeit senden könnte
Es gibt Ereignisse A und C (s. Abb. 250), für die in S gilt τC > τA und in S´ gilt τC´ < τA´. Diese Tatsache erweckt zunächst den Eindruck, in der Relativitätstheorie sei die Kausalität verletzt. Um das zu verdeutlichen, werden zwei Ereignisse A und B (Arbeit und Bericht) betrachtet (Abb. 251), die in S nacheinander liegen. Wenn es gelänge, von B aus eine Nachricht nach
C , das in S´ ruht, zu schicken und von dort nach A, wobei das Signal von B nach C in S betrachtet und das Signal von C nach A von S´aus betrachtet mit positiver Zeitrichtung liefe,
könnte man in A Informationen über die Zukunft erhalten (oder die Vergangenheit beeinflussen). Da solche Möglichkeit unser Weltbild erheblich stören würde, schließt man derartige Signale aus. Im Minkowski Diagramm haben sie Steigungen < 1 und damit Geschwindigkeiten
v > c. Um die Kausalität zu wahren, dürfen in der Relativitätstheorie keine Signale mit v > c
möglich sein. Es gibt daher auch keine starren Körper.
Abb. 252: In der Relativitätstheorie muß neu definiert werden, was Vergangenheit, Gegenwart und Zukunft heißt.
Abb. 252 zeigt einen Minkowski Raum mit zwei Ortskoordinaten. In ihm liegen alle Ereignisse, die von A beeinflußbar sind, in einem Kegel mit der Steigung 1 um die positive τ - Achse.
Der Raum, der innerhalb dieses Kegels liegt, umfaßt alle Ereignisse, die in der Zukunft von A
231
Liegen. Die Ereignisse in einem Kegel um die negative τ - Achse können A beeinflussen. Sie
bilden die Vergangenheit von A. Alle Ereignisse, die zwischen den Kegeln liegen, können A
nicht beeinflussen und von A nicht beeinflußt werden. Sie bilden die Gegenwart. Gegenwärtige Ereignisse können durch geeignete Lorentz Transformationen so transformiert werden, daß
die Reihenfolge der Zeitpunkte sich umkehrt. Abstände zwischen gegenwärtigen Ereignissen
sind raumartig, die übrigen zeitartig.
δ) Der relativistische Doppler Effekt
Im System S sei ein Sender, der im Abstand TS Signale aussendet. Wenn der Sender sich mit
der Geschwindigkeit v vom Empfänger entfernt, treffen die Signale um ∆TS = vTS/c später ein,
da ihre Laufzeit sich durch die zusätzliche Entfernung vTS erhöht. Der Empfänger mißt die Signale also im Zeitabstand
T E = T S + vc T s =  1 + vc  T s
Wegen der Zeitdilatation geht die Senderuhr langsamer
TS =
T /S
1 − v 2 /c 2
Setzt man dies in die Gleichung für TE ein, erhält man
TE =
T /S
1 + vc
1 − v 2 /c 2
T E = T /S 1 + v/c
1 − v/c
(14)
Hiermit läßt sich die Frequenzverschiebung von Licht berechnen, das von einer Quelle ausgeht, die sich relativ zum Beobachter mit der Geschwindigkeit v bewegt.
ε) Ein Zwillingsparadoxon
Es werde ein Zeitvergleich zwischen einer in einem Inertialsystem ruhenden Uhr A und einer
zweiten B durchgeführt, die sich mit konstanter Geschwindigkeit v fortbewegt, umkehrt und
mit gleicher Geschwindigkeit zurückkommt. Die Zeit für das Umkehren der Geschwindigkeitsrichtung soll so kurz sein, daß sich in Ihr die Anzeige der Uhren nicht ändert. Wegen der
Zeitdilatation müssen wir folgern, daß bei der Rückkehr die Uhr B eine kleinere Zeit als die
Uhr A anzeigt. Stellt man sich vor, daß A und B eineiige Zwillinge seien, so muß man folgern,
232
daß nach der Rückkehr B Jünger als A ist. Um Die Ursache für diese paradox erscheinende
Behauptung zu verfolgen, diskutieren wir ein konkretes Beispiel.
Wir betrachten Zwillinge A und B, von denen B sich mit der Geschwindigkeit v/c = 3/5 2,5
Jahre lang(von der Erde aus gemessen) von A entfernt und innerhalb von 2,5 Jahren zurückkommt, so daß er insgesamt von A aus gesehen tA = 5 Jahre unterwegs ist. Die Uhr von B
zeigt dann
Abb. 253: Die von B ausgesandten Signale.
Abb. 254: Die von A ausgesandten Signale.
t B = t A 1 − v 2 /c 2 = t A 1 − 9/25 = 4 Jahre an.
Um ihr Alter zu vergleichen senden sie in gleichen Abständen, etwa alle Jahre Signale aus.
Das nach einem Jahr von der Erde ausgesandte Signal erreicht B wegen des Dopplereffektes
nach der Zeit
TB =
1 + v/c T =
E
1 − v/c
1 + 3/5 = 2 Jahre
1 − 3/5
d.h. genau auf der Hälfte der Reise. In dieser Zeit hat B zwei Signale ausgesandt, die A in den
ersten vier Jahren erreichen. Auf dem Rückflug sendet A vier Signale. In der Formel für den
Dopplereffekt ersetzt man v durch -v. Der Zeitabstand der in B empfangenen Signale ist dann
233
T B = T A 1 − v/c = T A 1 = 1 Jahr
2 2
1 + v/c
d.h. die vier Signale werden in den 2 Jahren des Rückfluges empfangen, während B noch zwei
Abb. 255: Die Zeitdilatation kann man mit Atomuhren im
Flugzeug direkt messen.
Signale aussendet, die von A im letzten Jahr empfangen werden. Die Verhältnisse sind in den
Abb. 253 und 254 in Minkowski Diagrammen dargestellt. A sendet also fünf Signale, von denen B eins auf dem Hinflug und vier auf dem Rückflug empfängt. B sendet vier Signale aus,
von denen zwei A in den ersten 4 Jahren und zwei im letzten Jahr empfängt. Der Weltraumreisende B ist also nach der Rückkehr um ein Jahr jünger als sein stationärer Zwillingsbruder A.
Durch die mitgeteilten Signale kennt jeder das Alter des anderen.
e) Experimente mit Uhren
1971 machten Hafele und Keating ein Experiment, bei dem sie mit vier kommerziellen Atomuhren in Linienflugzeugen einmal in westlicher und einmal in östlicher Richtung die Welt
umflogen und die Anzeige der bewegten und stationär auf der Erde verbliebenen Uhren miteinander verglichen. Zur Berechnung des erwarteten relativistischen Effektes betrachtet man
das System von einem Inertialsystem aus. Die Bewegung der Uhr auf der Erde durch deren
Rotation und ein Gravitationseffekt aus der allgemeinen Relativitätstheorie, der von der gleichen Größenordnung wie der Geschwindigkeitseffekt ist, müssen mit berücksichtigt werden.
1975 - 76 führte eine Gruppe aus Maryland eine Präzisionsmessung durch. Atomuhren wurden über Zeiten von 15 - 20 Stunden in 10 km Höhe geflogen. Der Gang der Uhren wurde
durch Laserblitze übertragen. Die Flugbahn wurde mit Radar überwacht. Aufgrund des Gravitationseffektes gehen in dieser Zeit die Flugzeuguhren um 53ns schneller, aufgrund des Geschwindigkeitseffektes um 6ns langsamer. Es ergab sich eine Übereinstimmung mit dem theoretischen Effekt mit einer Meßunsicherheit von etwa 1,6%.
Der Gravitationseffekt ist ein Effekt der allgemeinen Relativitätstheorie. Seine Größe kann
man ableiten, wenn man weiß, daß die Energie eines Photons
E = hν
234
ist, mit h = 6,6·10-34Js. Seine Masse ist gegeben durch mc2 = E, also m = hν/c2. Der Unterschied in potentieller Energie im Gravitationsfeld ist
∆E pot = mgH = hν2 gH
Man nimmt an, daß die Energieabnahme des Photons gleich der Differenz der durchlaufenen
potentiellen Energie ist.
∆E = h∆ν = 2hν
c gH
∆ν = ∆t = Hg
2
ν
t
Da man das Licht als eine spezielle Uhr ansehen kann, deren Zeitanzeige durch die Anzahl der
Perioden des Lichts gegeben ist, kann man Licht zum Vergleichen zweier Uhren in unterschiedlicher Höhe verwenden. Um den Gang der Uhr A im Tal der Station B auf dem Berg
mitzuteilen, wird Licht von A nach B gesandt. Dabei verliert es Energie und damit Frequenz.
Die Uhr im Tal scheint also langsamer zu gehen.
f) Experimente mit Elementarteilchen
Die Zahl zerfallender Elementarteilchen nimmt exponentiell ab wie beim radioaktiven Zerfall.
Nach einer Halbwertszeit tH ist nur noch die Hälfte der anfänglichen Teilchenzahl vorhanden.
Myonen sind elektronenartige Teilchen mit einer Masse mµ =206 me, die mit einer Halbwertszeit tH = 1,52 µs in ein Elektron und zwei Neutrinos zerfallen.
µ− → e− + νe + νµ
1941 entdeckten Rossi und Hall, daß Myonen, die durch kosmische Strahlung am oberen
Rand der Atmosphäre erzeugt werden und auf die Erdoberfläche fallen, eine längere Halbwertszeit haben als ruhende Myonen. Sie würden ohne Zeitdilatation die Erdoberfläche nicht
erreichen. Von den Myonen aus gesehen wird die Dicke der Erdatmosphäre kontrahiert.
Quantitativ wurden Experimente mit Myonen an Beschleunigern durchgeführt (z.B. Meyrin,
Cern). Man bringt Myonen auf eine Geschwindigkeit 0,99942·c. Nach der Reletivitätstheorie
ist dann die Lebensdauer
235
τ=
τ0
1 − v 2 /c 2
= 44, 6µs
Das Experiment gab Übereinstimmung innerhalb einer Fehlergrenze von 0,2%.
g) Andere Evidenzen
Heute ist der Beitrag relativistischer Effekte nicht nur im wissenschaftlichen Interesse, sondern er muß bei einer ganzen Reihe von technischen Geräten berücksichtigt werden, damit
diese ordnugsmäßig funktionieren. Bei der Funknavigation ist die erforderliche Genauigkeit
nur auf grund der Unabhängigkeit der Lichtgeschwindigkeit vom Referenzsystem möglich.
Teilchenbeschleuniger müssen die Massenzunahme der Teilchen berücksichtigen, um im richtigen Moment beschleunigende Felder anzuwenden.