Geometrie: Punktspiegelung Klasse 7DaF April 2008 Wir spiegeln

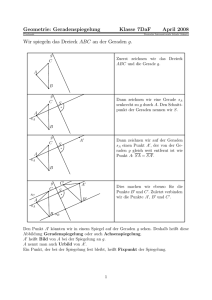
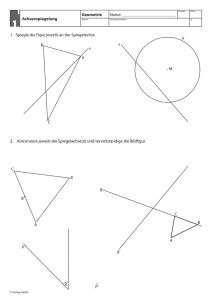
Geometrie: Punktspiegelung
Klasse 7DaF
Gierhardt
April 2008
Deutsche Internationale Schule Jakarta
Wir spiegeln das Dreieck ABC an dem Punkt Z.
C
b
Z
A
b
b
B
b
Dann zeichnen wir eine Gerade g
durch A und Z.
C
b
A
b
g
b
Z
b
B
b
b
Zuerst zeichnen wir das Dreieck
ABC und den Punkt Z. Z heißt auch
Zentrum.
C
A
b
g
b
Z
b
b
A′
B
b
b
Jetzt zeichnen wir auf der Geraden g
einen Punkt A′ , der vom Zentrum Z
gleich weit entfernt ist wie Punkt A:
ZA = ZA′ . Z soll dabei die Strecke
AA′ halbieren.
B′
Dies machen wir ebenso für die
Punkte B ′ und C ′ . Zuletzt verbinden
wir die Punkte A′ , B ′ und C ′ .
C
A
g
b
Z
b
b
b
A′
C′
B
Diese Abbildung heißt Punktspiegelung.
A′ heißt Bild von A bei der Spiegelung an Z.
A nennt man auch Urbild von A′ .
Ein Punkt, der bei der Spiegelung fest bleibt, heißt Fixpunkt der Spiegelung.
1
Aufgaben:
1. Spiegle alle Punkte und Figuren am Punkt Z.
b
C
a
b
b
b
A
B
c
b
b
b
D
F
Z
b
G
2. Spiegle einen Winkel von 35◦ am Scheitelpunkt.
3. Spiegle ein Rechteck an einem Eckpunkt.
4. Spiegle ein Rechteck am Schnittpunkt der Diagonalen.
5. Welche Figur erhält man, wenn man irgend eine punktsymmetrische Figur am Zentrum
spiegelt?
6. Wo liegen alle Fixpunkte der Punktspiegelung in Aufgabe 1?
7. Schreibe alle punktsymmetrischen (Druck)-Buchstaben des Alphabets auf.
-e Punktspiegelung, -en
-s Zentrum, Zentren
spiegeln an (einem Punkt)
halbieren
2