Spiegelung an Dreiecken

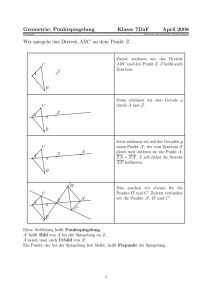
Tobias Schoel
LSGM
27. Februar 2006
Spiegelung an Dreiecken
1
Spiegelung von Punkten an Dreiecken
1.1
Bemerkung zur Aufgabe 450833 - LMO 2006
?Aufgabe 450833:
Drei kongruente Kreise mit den Mittelpunkten M1 , M2 , M3 und dem Radius r verlaufen durch einen Gemeinsamen Punkt D. Diese Kreise schneiden
einander außerdem in weiteren Punkten, die mit A, B und C bezeichnet
werden.
a. Beweise, dass man einen Punkt S konstruieren kann, der von diesen
drei Schnittpunkten den gleichen Abstand besitzt!
b. Vergleiche den Radius des Kreises mit dem Mittelpunkt, auf dem A, B
und C liegen, mit dem Radius r!
Die Teilaufgabe a. lässt viele Möglichkeiten in Hinsicht auf den (inhaltlichen) Umfang
der Lösung. Um rigoros zu sein, müsste man beweisen, dass die Punkte A, B und C
nicht auf einer Geraden liegen. Dies würde wohl eine ganz eigene Aufgabe sein. Dieser
Punkt S existiere also und ist damit der Umkreismittelpunkt des Dreiecks 4ABC und
der mit r zu vergleichende Radius ist der Umkreisradius ρ dieses Dreiecks.
Wie man schnell vermuten wird, sind diese beiden Radien gleich groß. Die Musterlösung
führt einen Beweis über die zahlreichen Rhomben, die sich ergeben, wenn man alle bekannten Radien einzeichnet. Dieser Beweis ist an sich recht elegant und leicht einzusehen,
jedoch schwer zu finden. Jedenfalls wurde er von keinem thüringer Teilnehmer dieser Altersklasse gefunden. Es wurde hingegen von einem Schüler eine Beweisidee gefunden, die
meiner Meinung nach eleganter ist und die Bedeutung von Geometrie in mathematischen
Zirkeln unterstreicht, da die Ideen sehr nah bei den Inhalten solcher Zirkel insbesondere
der Thematik Euler’sche Gerade und Feuerbach’scher Kreis“ 1 liegen.
”
Kernpunkt des Beweises ist folgendes Lemma:
Lemma von Startnummer 840:
Sei U der Umkreismittelpunkt von 4P QR und seien P 0 , Q0 und R0 die
Bildpunkte von U bei Spiegelung an den Seiten QR, P R und P Q. Seien
weiterhin P 00 , Q00 und R00 die Bilder von P , Q und R bei Spiegelung an U .
Dann gehen 4P 0 Q0 R0 und 4P 00 Q00 R00 durch Verschiebung ineinander über.
Insbesondere gilt 4P 0 Q0 R0 ∼
= 4P QR.
Beweis: Da U der Umkreismittelpunkt ist, sind liegen nach Konstruktion U P 0 ,U Q0
und U R0 auf den Mittelsenkrechten von 4P QR und die Mittelpunkte dieser Strecken sind die Seitenmittelpunkte von 4P QR. Das bedeutet, 4P 0 Q0 R0 geht aus dem
1
Für weitere Informationen zu diesem Thema siehe auch Euler’sche Gerade und Feuer”
bach’scher Kreis“ von Hans-Gert Gräbe, Mathematische Bibliothek der LSGM: http://lsgm.unileipzig.de/KoSemNet/pdf/graebe-99-1.pdf.
1
Tobias Schoel
LSGM
27. Februar 2006
Seitenmittelpunktsdreieck von 4P QR durch zentrische Streckung mit Streckfaktor 2
und Streckzentrum U hervor. Da das Seitenmittelpunktsdreieck wiederum aus 4P QR
durch zentrische Streckung mit Streckfaktor − 12 und Streckzentrum S hervorgeht, gilt
4P 0 Q0 R0 ∼
= 4P QR. Außerdem sind die Seiten von 4P QR und 4P 0 Q0 R0 paarweise
parallel. Damit ist die zweite Teilaussage bewiesen. Der weitere Beweisverlauf orientiert
sich an der Euler’schen Gerade. Es muss eine zentrische Streckung mit dem Streckfaktor
−1, also eine Punktspiegelung, geben, die 4P QR in 4P 0 Q0 R0 überführt. Bekanntermaßen ist U als Umkreismittelpunkt gleichzeitig Höhenschnittpunkt des Seitenmittelpunktsdreiecks und damit auch Höhenschnittpunkt von 4P 0 Q0 R0 . D.h. bei der gesuchten
zentrischen Streckung bzw. Punktspiegelung, geht U in den Höhenschnittpunkt H von
4P QR über. Das gesuchte Streck- bzw. Spiegelungszentrum ist also der Mittelpunkt N
der Strecke U H: der Mittelpunkt des Feuerbachkreises von 4P QR.
Das heißt, die Dreiecke 4P 0 Q0 R0 und 4P 00 Q00 R00 gehen durch Punktspiegelung aus
4P QR hervor, und lassen sich damit durch Verschiebung ineinander überführen.
Was hat dieser Satz nun mit der eigentlichen Aufgabe zur tun? Da die drei Kreise den
gleichen Radius r haben, ist D der Umkreismittelpunkt von 4M1 M2 M3 . Außerdem gehen die Punkte A, B und C aus D durch Spiegelung an den Seiten dieses Dreiecks hervor
(Elementarer Zusammenhang zwischen den beiden Schnittpunkten zweier Kreise). Das
Lemma lässt sich also in dieser Situation anwenden und es gilt 4M1 M2 M3 ∼
= 4ABC.
Damit sind insbesondere die Umkreisradien beider Dreiecks gleich.?
1.2
Ähnliches Verhalten
Nachdem der Zusammenhang des Lemmas von Startnummer 840 bewiesen ist, stellt sich
sofort folgende Frage:
Frage: Gibt es weitere Punkte X, die bei Spiegelung an 4P QR auf dazu
kongruente Dreiecke 4Xp Xq Xr abgebildet werden? Wenn ja, wie lassen sie
sich beschreiben?
2
Spiegelung von Geraden an Dreiecken
Spiegelt man eine Gerade an den drei Seiten eines Dreieckes, so entstehen drei neue
Gerade, die (meistens) ein neues Dreieck bilden. Allerdings scheint dieses Dreieck nicht
so einfach zu beschreiben zu sein, wie das Bild eines Punkt. Auch hier stellt sich eine
ähnliche Frage:
Frage: Gibt es Geraden, die bei Spiegelung an einem Dreieck auf dazu
ähnliche (kongruente) Dreiecke abgebildet werden. Wenn ja, wie lassen sie
sich beschreiben?
2