Hall-Effekt
Werbung

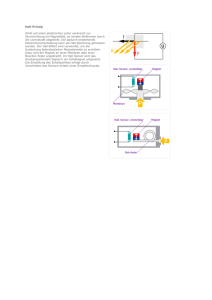
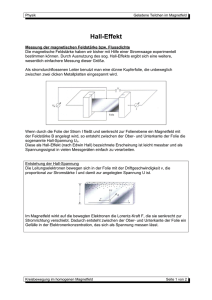
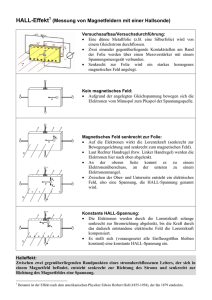
Hall-Effekt Lars Leschewitz [email protected] Jonas Bories [email protected] Tutor: Till Kolster 14. Dezember 2015 Physikalisches Grundpraktikum II Semesterkurs WS 2015/16 Versuch: Nr. 8 Versuchstag: 09.12.2015 Inhaltsverzeichnis 1 Physikalische Grundlagen 1 1.1 Kräfte auf bewegte Ladungsträger . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1.2 Hall-Effekt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1.3 Hall-Spannung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 2 Aufgaben 3 3 Versuchsdurchführung 4 3.1 Geräte und Komponenten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 3.2 Fehlerrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 3.3 Messung des Magnetfeldes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 3.4 Aufgabe 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 3.4.1 Durchführung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 3.4.2 Auswertung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 3.5 Aufgabe 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 3.5.1 Durchführung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 3.5.2 Auswertung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 3.6 Aufgabe 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 3.6.1 Durchführung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 3.6.2 Auswertung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13 4 14 Zusammenfassung und Disskussion Literatur A Anhang A.1 Handschriftliches Messprotokoll I II . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ii II 1 Physikalische Grundlagen 1.1 Kräfte auf bewegte Ladungsträger Neben der Coulomb-Kraft, welche auf jegliche elektrische Ladung wirkt, die sich in einem elektrischen Feld befindet, kommt bei bewegten Ladungsträgern in einem magnetischen Feld die Lorentz-Kraft hinzu[1, S. 347] . Abbildung 1.1 stellt die Wirkrichtungen der beiden Kräfte dar. Im folgenden soll die Lorentzkraft F~L näher betrachtet werden, sie bildet mit dem Geschwingigkeitsvektor ~v und dem Feld~ ein Rechtssystem und ist wie die Coulomb-Kraft proportional vektor der magnetischen Flussdichte B zur Ladung q. ~ F~L = q · (~v × B) (1.1) Abbildung 1.1: Coulomb-Kraft und Lorentz-Kraft, Quelle:Gerthsen Physik[1, S. 347] 1.2 Hall-Effekt Der Hall-Effekt (nach dem Entdecker Edwin Hall, 1879) beschreibt eine Häufung von Ladungsträgern, die eine Gegenkraft der Lorentz-Kraft zur Folge hat. ~ H = −q · (~v × B) ~ q·E (1.2) In einem Leiter der Höhe h (in Richtung der Lorentz-Kraft) bedingt das Querfeld ~ H = −~v × B ~ E (1.3) eine Querspannung, die sogenannte Hall-Spannung UH [1, S. 350] . ~ UH = −h · |~v × B| 1 (1.4) 1.3 Hall-Spannung Über die Äquivalenz der Stromdichte von Strom pro Fläche (Höhe h mal Dicke d) zu dem Produkt aus der Ladungsträgerdichte n, deren Ladungen q und dem Geschwindigkeitsvektor ~v I I J~ = = = q · n · ~v A h·d (1.5) kann die Hall-Spannung in die folgende pragmatische Form UH UH I ~ · |B| q·n·h·d ~ ~ 1 I · |B| I · |B| = − · = −AH · q·n d d = −h · gebracht werden, wobei der Term AH = 1 q·n (1.6) (1.7) von der Temperatur und dem Leiterwerkstoff abhängig ist und als Hall-Konstante bezeichnet wird. Die geometrische Darstellung nach Gerthsen[1, S. 350] kann auf Abbildung 1.2 nachvollzogen werden. Abbildung 1.2: Hall-Spannung, Quelle:Gerthsen Physik[1, S. 350] Das Vorzeichen des Hall-Koeffizienten entspricht dem bestimmenden Anteil der Ladungsträger. Überwiegt der Anteil der Elektronen ist AH negativ, bei vorrangig duch Löcher transportierte Ladung in einem p-dotierten Halbleiter ist AH positiv. Außerdem ist direkt ersichtlich, dass AH bei gut leitenden Leiterwerkstoffen sehr klein ist. Für die Konstruktion eines Hall-Sensors (auch Hall-Sonde oder Hall-Generator) sind III-V Halbleiter besonders gut geeignet, weil die hohe Ladungsträgerbeweglichkeit (der Betrag der Driftgeschwindigkeit |~v |) dieser Werkstoffe zu einem großen Hall-Koeffizienten und damit zu einer großen Empfindlichkeit des Sensors führt.[1, S. 350] . 2 2 Aufgaben 1. Beobachtung des Hall-Effektes an Germanium (n-Ge oder p-Ge) als Funktion von Steuerstrom und Magnetfeld. Berechnung der Hall-Konstanten von Germanium. Bestimmung von Art und Konzentration der Ladungsträger. 2. Untersuchung der Temperaturabhängigkeit der Hall-Spannung bei Germanium und Berechnung der Bandlücke. 3. Aufgabe zur gemeinsamen Durchführung: Beobachtung des Hall-Effektes bei Cu und Zn. Abschätzung der Hall-Konstanten sowie von Art und Konzentration der Ladungsträger. 3 3 Versuchsdurchführung 3.1 Geräte und Komponenten • Platinen mit Materialproben (n-Ge, p-Ge, Cu und Zn) (Dicke: dGe = 1 mm ± 3 %) (Dicke: dCu = 18 µm ± 10 %) (Dicke: dZn = 20 µm ± 10 %) • Labornetzteil • Elektromagnet aus zwei Spulen und einem U-förmigem Eisenkern mit Polschuhen • Digital-Multimeter Fluke 175 (Messungenauigkeit im verwendeteten Messbereich bis 600 mV = 0, 15 %) • Digital-Multimeter Voltcraft VC230 (Messungenauigkeit im verwendeteten Messbereich bis 20 A = 1, 2 %) • Labor-Multimeter Hameg HM8112-3 (Messungenauigkeit im verwendeteten Messbereich bis 0, 1 V = 0, 005 %) • Knick Mikrovoltmeter (Messung praktisch fehlerfrei) 3.2 Fehlerrechnung Sofern nicht anders angegeben, werden sämtliche Fehler konsequent nach den Gauß’schen Fehlerfortpflanzungsgesetzen[2, S. 10 f.] berechnet. 3.3 Messung des Magnetfeldes ~ ist im Labor für den HAL-Versuch Ein Magnetometer zur Messung der magnetischen Flussdichte |B| nicht verfügbar. Stattdessen wird der erzeugende Spulenstrom IB gemessen und daraus indirekt die Flussdichte berechnet. Der Zusammenhang wird in Form eines Graphen vom Labor gestellt und entspricht der linearen Funktion: ~ = B = 136 |B| mT · IB + 5 mT ± 5 mT A 4 (3.1) 3.4 Aufgabe 1 3.4.1 Durchführung Die Platine mit einem n-Ge Kristall wird rechtwinklig und mit etwa gleichen Abständen der Seitenfächen zu dem Polschuhen in dem Elektromagnet arretiert. Die Anschlüsse für den Spulenstrom, den Steuerstrom und die Hall-Spannung werden kontaktiert und kontrolliert, bevor die Netzteile eingeschaltet werden. In der ersten Messreihe wird die Remanenz mit dem maximalen Spulenstrom von 3 A hergestellt und das Netzteil für den Spulenstrom wieder heruntergeregelt und ausgeschaltet, sowie das Voltmeter für die Hall-Spannung genullt. Anschließend werden Steuer- und Spulenstrom für die drei Messreihen durchgestimmt. Die Daten der Messreihen können dem Anhang entnommen werden. Spulenstrom und der Steuerstrom werden mit je einem Digital-Multimeter Voltcraft VC230, die Hall-Spannung wird mit dem Labor-Multimeter Hameg HM8112-3 gemessen. Die Messunsicherheit der Hall-Spannung fällt in allen Messreihen mindestens zwei Größenordnungen geringer aus und wird daher in der Auswertung vernachlässigt. Abbildung 3.1: Messaufbau, Skizze 5 3.4.2 Auswertung Für die erste Teilaufgabe, die Beobachtung des Halleffektes als Funktion von Steuerstrom und Magnetfeld, werden die Messdaten, samt linearer Regression grafisch dargestellt. Die zweite Teilaufgabe, die Berechnung der Hall-Konstanten von Germanium, erfolgt unter Verwendung von Fromel 1.7 und Umstellung nach AH . AH = − UH · d IS · B (3.2) Für die dritte Teilaufgabe, die Bestimmung von Art und Konzentration der Ladungsträger, kann den Messdaten direkt entnommen werden, dass die negative Hallspannung der Verwendung eines n-dotierten Gemaniumkristalls und damit dem Ladungstransport durch Elektronen entspricht. Die Ladungsträgerdichte wird unter Verwendung und Umformung von Formel 1.7 berechnet. n=− IS · B UH · d · q (3.3) Die magnetische Flussdichte wird jeweils nach Formel 3.1 durch die Beziehung zum Spulenstrom ersetzt. 6 Beobachtung des Halleffektes Abbildung 3.2: Messreihe 1, IS über UH bei IB = 0 A Die erste Messreihe liefert eine Hall-Spannung bei einem konstanten Spulenstrom von 0 A, dieser Effekt ist in der Remanenz der Spule begründet und fließt als Korrektur in die Berechnung der Hall-Konstanten in Teilaufgabe 2 ein. Die Parameter aus der linearen Regression können Tabelle 3.1 entnommen werden. Die obere und untere Grenzgerade sind aufgrund ihrer Nähe zur Funktionsgraden im Plot nicht zu erkennen. Tabelle 3.1: Parameter der linearen Regression für IS über UH bei IB = 0 A Steigung Ordinatenabschnitt A A a = −3, 839 V ± 0, 005 V b = 0, 116 mA ± 0, 039 mA 7 Abbildung 3.3: Messreihe 2, IB über UH bei IS = 30 mA Tabelle 3.2: Parameter der linearen Regression für IB über UH bei IS = 30 mA Steigung Ordinatenabschnitt kA a = −20, 065 kA V ± 0, 744 V b = −157, 753 A ± 5, 916 A 8 Abbildung 3.4: Messreihe 3, IS über UH bei IB = 2 A Tabelle 3.3: Parameter der linearen Regression für IS über UH bei IB = 2 A Steigung Ordinatenabschnitt A A a = −3, 769 V ± 0, 005 V b = 0, 169 mA ± 0, 039 mA 9 Berechnung der Hall-Konstanten Nach Formel 3.2 und 3.1 ergibt sich die Hall-Konstante wie wie folgt: v u AH 2 u ∂A UH · d H =− · ∆d ±t mT ∂d IS · (136 A · IB + 5 mT) + ∂AH · ∆IS ∂IS 2 + ∂AH · ∆IB ∂IB 2 (3.4) Nach Messreihe 2 gilt für IB aus der linearen Regression: IB (UH ) = a · UH + b = kA kA ± 0, 744 − 20, 065 V V · UH + (−157, 753 A ± 5, 916 A) (3.5) Die Remanenzkorrektur aus Messreihe 1 trägt den folgenden festen Betrag zur Hall-Spannung bei: UH,kor = 1 1 · 30 mA = −7, 815 mV · IS = A a −3, 839 V (3.6) Damit ergibt sich die Hall-Konstante nach Messreihe 2 zu: AH (UH , IB ) = − 3 3 (UH + UH,kor ) · d −5 m −8 m = 1, 23 · 10 ± 5, 37 · 10 C C 30 mA · (136 mT A · IB + 5 mT) (3.7) Nach Messreihe 3 gilt für IS aus der linearen Regression: IS (UH ) = a · UH + b = A A − 3, 769 ± 0, 005 V V · UH + (0, 169 mA ± 0, 039 mA) (3.8) Die Remanenzkorrektur aus Messreihe 1 trägt den folgenden variablen Betrag zur Hall-Spannung bei: IS,kor = a · UH + b = −3, 839 A · UH + 0, 116 mA V (3.9) Damit ergibt sich die Hall-Konstante nach Messreihe 3 zu: AH (UH , IS ) = − (UH + UH,kor ) · d m3 m3 = 4, 75 · 10−4 ± 4, 29 · 10−6 mT C C IS · (136 A · 2 A + 5 mT) (3.10) Mangels verfügbarer Fachbücher kann kein verlässlich referenzierbarer Literaturwert ermittelt werden. Unsichere Quellen im Internet[3][4] nennen vermehrt AH,Ge = 5 · 10−3 m3 C bei Zimmertemperatur. Im Vergleich zu dieser Angabe sind beide Werte als signifikant unterschiedlich anzusehen. Konzentration der Ladungsträger Mit qElektron = −1, 602 · 10−19 C und Formel 3.3 ergeben sich folgende Ladungsträgerdichten: nM essreihe2 = 5, 11 · 1023 1 1 ± 1, 21 · 1023 3 m3 m (3.11) nM essreihe3 = 6, 52 · 1021 1 1 ± 1, 52 · 1021 3 m3 m (3.12) 10 3.5 Aufgabe 2 3.5.1 Durchführung Der Messaufbau aus Aufgabe 1 wird um die Kontaktierung der Widerstandsheizung und des Thermoelements erweitert. Vor Beginn der Messung wird die Raumtemperatur an einem Zimmerthermometer mit 20 °C = 293, 15 K abgelesen, die Thermospannung beträgt zu diesem Zeitpunkt 0 V. Die Heizung wird gemäß der Laborvorgabe mit 6 V Wechselspannung betrieben und zur Sicherheit bei 4 mV Thermospannung abgeschaltet. Der Messaufbau wird mit IB = 2 A und IS = 30 mA betrieben. Die Wertepaare werden nach Abwarten des Drifts der Thermospannung bei fallender Temperatur aufgenommen. Die Daten der Messreihen können dem Anhang entnommen werden. Die Thermospannung wird mit einem Digital-Multimeter Fluke 175 gemessen. 3.5.2 Auswertung Die Daten wurden in zwei Messreihen von UT = 3, 8 mV bis 3, 1 mV und UT = 2, 6 mV bis 1, 5 mV aufgezeichnet. Auf Abbildung 3.5 ist zu erkennen, dass die zweite Messreihe (Messpunkte unten) offensichtlich keinen linearen Zusammenhang darstellt. Es ist zu Vermuten, dass der Wärmefluss durch die Platine die Messdaten der zweiten Messreihe verfälscht hat. Es werden im Folgenden nur die Messdaten der ersten Messreihe ausgewertet (Messpunkte oben). Abbildung 3.5: beide Messreihen, UH über UT 11 Die Thermospannung wird gemäß des Temperaturkoeffizienten des Thermoelements von 40 µV K in die Temperatur umgesetzt. T = 293, 15 K + 1 40 µV K (3.13) · UT Die Ladungsträgerdichte n nach Formel 3.3 wird als Arrheniusgraph logarithmiert gegen den Kehrwert der Temperatur aufgetragen, siehe Abbildung 3.6. Abbildung 3.6: Arrheniusgraph, ln(n) über 1/T der ersten Messreihe UT über UH Tabelle 3.4: Parameter der linearen Regression des Arrheniusgraph, ln(n) über 1/T Steigung Ordinatenabschnitt a = 2759, 51 K ± 118, 5 K b = 59, 8553 ± 0, 3125 Unter Verwendung der im Laborvorgespräch hergeleiteten Formel folgt aus der Steigung a der linearen Regression und der Boltzmann-Konstante kB = 8, 617 · 10−5 eV K der Betrag der Bandlücke: v u 2 u ∂∆E Ge ∆EGe = 2 · kB · a ± t · ∆a = 0, 476 eV ± 0, 020 eV ∂a (3.14) Im Vergleich mit dem Literaturwert[5] von 0, 67 eV bei 300 K ist dieser Wert als signifikant unterschiedlich anzusehen. 12 3.6 Aufgabe 3 3.6.1 Durchführung An einem separaten Messplatz wird, gemeinsam von allen Laborteilnehmern, ein zu Aufgabe 1 äquivalenter Messaufbau mit einem Mikrovoltmeter anstelle des Labor-Multimeters zur Messung der Hall-Spannung aufgebaut. Außerdem wird dem Anschluß der Steuerspannung ein Vorwiderstand vorgeschalten. Für je eine Platine mit einem Kupfer- und einem Zinkstreifen wird bei konstanten Magnetfeld die Abhängigkeit der Hall-Spannung vom Steuerstrom aufgezeichnet. Die Daten der Messreihen können dem Anhang entnommen werden. 3.6.2 Auswertung Aus den Messdaten ist qualitativ direkt ersichtlich, dass beide metallische Leiter Hall-Spannungen in einer erwartungsgemäß geringen Größenordnung aufweisen und damit auch deren Hall-Konstanten in einer geringeren Größenordnung als der untersuchte Halbleiter Germanium liegen müssen. Es verwundert jedoch, das Zink eine positive Hall-Konstante aufweist. Diese Beobachtung deckt sich mit den Literaturangaben nach[6] , bei Zimmertemperatur ist für Kupfer AH,Cu = −5, 3 · 10−11 und für Zink AH,Zn = +6, 4 · 10−11 m3 C m3 C angegeben. Eine Störstellenleitung durch Löcher kann bei einem Leiter ausgeschlossen werden, eine Erklärung für das positive Vorzeichen ist weder ansatzweise im Internet, noch in der verfügbaren Literatur gegeben. Über die Konzentration der Ladungsträger kann mit einer geringen Hall-Spannung gemäß Formel 3.3 die qualitative Aussage getroffen werden, dass für einen Leiterwerkstoff eine erwartungsgemäß hohe Anzahl an Ladungsträgern vorhanden ist. 13 4 Zusammenfassung und Disskussion Im vorliegenden Laborprotokoll zum Hall-Effekt werden zunächst die theoretischen Grundlagen zur Beschreibung der physikalischen Vorgänge bei der Wirkung von elektrischen und magnetischen Feldern auf bewegte Ladungsträger behandelt. Im Hauptteil soll die direkte Abhängigkleit der HallSpannung vom Steuerstrom und die indirekte Abhängigkeit von der magnetischen Flussdichte über den Magnetstrom beobachtet und quantitativ ausgewertet werden. Dazu stehen explizite Platinen mit negativ oder positiv dotiertem Germanium, sowie Kupfer und Zink zur Verfügung, die in einen ~ B -charakterisierten Elektromagneten eingesetzt werden. Am laborseitig vorkonfigurierten und |B|-I Beispiel der Germaniumprobe werden im ersten Teil des Laborversuches die Hall-Konstante und die Ladungsträgerdichte experimentell ermittelt und mit dem Literaturwert verglichen. Im zweiten Teil des Laborversuches wird die Temperaturabhängigkeit der Hall-Spannung von Germanium sowie dessen Bandlücke untersucht und berechnet. Im letzten Teil erfolgt eine qualitative Betrachtung des Hall-Effektes sowie von Art und Konzentration der Ladungsträger anhand der Kupfer- und Zinkproben. Die Hall-Konstante des negativ dotiertem Germanium bei Zimmertemperatur wird in Abhängigkeit vom Magnetfeld mit 1, 23·10−5 3 4, 75 · 10−4 mC 3 ± 4, 29 · 10−6 mC m3 C ±5, 37·10−8 m3 C und in Abhängigkeit von der Steuerspannung mit ermittelt. Die Ergebnisse der beiden experimentellen Bestimmungen liegen eine Größenordnung auseinender und weichen vom Orientierungswert AH,Ge = 5 · 10−3 m3 [3][4] C bis zu zwei Größenordnungen ab. Sie sind damit nicht als vertrauenswürdig anzusehen, die Ursache hierfür ist unklar. Die resultierenden Ladungsträgerdichten 5, 11 · 1023 1021 m13 ± 1, 52 · 1021 m13 1 m3 ± 1, 21 · 1023 1 m3 und 6, 52 · sind. mit dem selben Fehler behaftet. Mögliche Fehler bei der Durchführung der Messungen können nicht ausgeschlossen werden. Das experimentelle Ergebnis für die Bandlücke von Germanium ist mit 0, 476 eV ± 0, 020 eV in der selben Größenordnung wie der Literaturwert[5] von 0, 67 eV bei 300 K, jedoch auch ausserhalb des dreifachen Fehlerintervalls. Die qualitative Betrachtung von Kupfer und Zink ergibt die erwartungsgemäß kleineren Größenordnungen bei den Beträgen der Hall-Spannung und der damit verknüpften Hall-Konstante, sowie der Ladungsträgerdichte. Jedoch verbleibt die beobachtete Anomalie von Zink mit einer negativen Hall-Spannung ungeklärt. 14 Literatur [1] Dieter Meschede, Hrsg. Gerthsen Physik. 23. Auflage Berlin: Springer, 2006. isbn: 978-3-54025421-8 (siehe S. 1, 2). [2] H. J. Eichler; H.-D. Kronfeldt; J. Sahm. Das Neue Physikalische Grundpraktikum. Zweite, erweiterte und aktualisierte Auflage Berlin: Springer, 2006. isbn: 978-3-540-21453-3 (siehe S. 4). [3] url: http://www.raschweb.de/PH11-Hall-Effekt.pdf (siehe S. 10, 14). [4] url: https://www.physnet.uni-hamburg.de/TUHH/Versuchsanleitung/Halleffekt. pdf (siehe S. 10, 14). [5] WP: Bandlücke. url: https://de.wikipedia.org/wiki/Bandl%C3%BCcke (siehe S. 12, 14). [6] WP: Hall-Konstante. url: https : / / de . wikipedia . org / wiki / Hall - Konstante (siehe S. 13). I