Hall-Effekt - Mossakowski

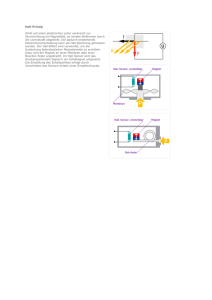
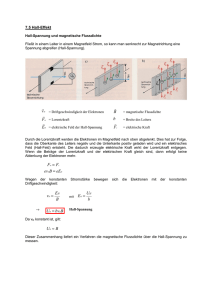
Physik
Geladene Teilchen im Magnetfeld
Hall-Effekt
Messung der magnetischen Feldstärke bzw. Flussdichte
Die magnetische Feldstärke haben wir bisher mit Hilfe einer Stromwaage experimentell
bestimmen können. Durch Ausnutzung des sog. Hall-Effekts ergibt sich eine weitere,
wesentlich einfachere Messung dieser Größe.
Als stromdurchflossenen Leiter benutzt man eine dünne Kupferfolie, die unbeweglich
zwischen zwei dicken Metallplatten eingespannt wird.
Wenn durch die Folie der Strom I fließt und senkrecht zur Folienebene ein Magnetfeld mit
der Feldstärke B angelegt wird, so entsteht zwischen der Ober- und Unterkante der Folie die
sogenannte Hall-Spannung UH.
Diese als Hall-Effekt (nach Edwin Hall) bezeichnete Erscheinung ist leicht messbar und als
Spannungssignal in vielen Messgeräten einfach zu verarbeiten.
Entstehung der Hall-Spannung
Die Leitungselektronen bewegen sich in der Folie mit der Driftgeschwindigkeit v, die
proportional zur Stromstärke I und damit zur angelegten Spannung U ist.
Im Magnetfeld wirkt auf die bewegten Elektronen die Lorentz-Kraft F, die sie senkrecht zur
Stromrichtung verschiebt. Dadurch entsteht zwischen der Ober- und Unterkante der Folie ein
Gefälle in der Elektronenkonzentration, das sich als Spannung messen lässt.
Kreisbewegung im homogenen Magnetfeld
Seite 1 von 2
Physik
Geladene Teilchen im Magnetfeld
Berechnung der Hall-Spannung
Das so entstandene elektrische Hall-Feld hat die Feldstärke E H =
UH
b
. Dabei ist b die
Breite der Folie.
Die Elektronen der Ladung e werden so lange nach oben verschoben, bis die Lorentz-Kraft F
durch die elektrische Feldkraft FH des Hall-Feldes kompensiert wird:
F H =F
e⋅E H =e⋅v⋅B
UH
=v⋅B
b
Man kann also die Flussdichte über eine einfache Messung der Hall-Spannung bestimmen:
B=
UH
b⋅v
Faktoren der Hall-Spannung
Bei einer Teilchendichte n der Elektronen und dem Volumen V der Kupferfolie gilt für die
Stromstärke I:
ΔQ nVe nbdle
=
=
Δt
Δt
Δt
l
l
mit v=
⇒ Δt =
Δt
v
I =nbdve
I
v=
nbde
I=
Ersetzt man v in dem Ausdruck für UH, so folgt:
UH
b⋅v
U H =v⋅B⋅b
I⋅B⋅b
1 IB
UH=
= ⋅
n⋅b⋅d⋅e ne d
B=
Die Hall-Spannung UH ist von der Stromstärke I und der magnetischen Feldstärke B direkt proportional
abhängig. Die Foliendicke d und die Ladungsträgerdichte n beeinflusst die Hall-Spannung dagegen
umgekehrt proportional.
Um einen möglichst großen Hall-Effekt zu erzielen, muss man also die Ladungsträgerdichte sehr klein
und die Leiterfolie möglichst dünn wählen. Dadurch wird allerdings die mögliche Stromstärke stark
begrenzt. Als Ausgleich wählt man die Folienbreite b sehr groß.
Kreisbewegung im homogenen Magnetfeld
Seite 2 von 2