3.7. Hall-Effekt. Messung der magnetischen Flußdichte B

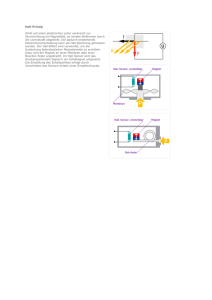
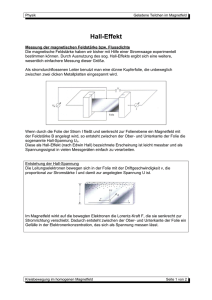
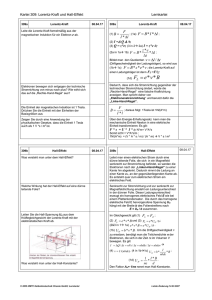
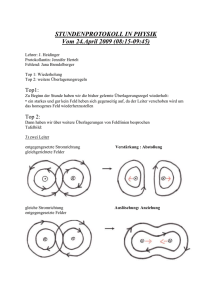
D.Michel
Vorlesung Experimentalphysik 2003/04
Teil 3: Elektrizitätslehre
3.7. Hall-Effekt. Messung der magnetischen Flußdichte B
Inhalt:
Wird ein äußeres Magnetfeld mit der magnetischen Induktion B senkrecht zur
Stromrichtung in einem Leiter orientiert, so tritt senkrecht zur Stromrichtung (l/|l|) und zur
Magnetfeldrichtung eine elektrische Feldstärke EH auf (Hall-Effekt). Dieser Effekt ist
verbunden mit der Lorentz-Kraft.
Anordnung: Eine metallische Platte befindet sich im Magnetfeld B. Durch Anlegen einer
äußeren Spannung fließt Strom I in Richtung l/|l| senkrecht zu B. Spannungsmessung an der
Platte senkrecht zu B und zu l
Hall-Effekt
a) Anordnung
→
Das Feld B zeigt in die Ebene
a)
b)
b) Zur Definition der Kräfte auf die
Ladungsträger Q = -e
Erklärung: Die Leitungselektronen mit Geschwindigkeit v, die entgegengesetzt zur
technischen Stromrichtung (l/|l|) gerichtet ist (übliche Konvention für die technische
Stromrichtung, der im äußeren Stromkreis von + zu - Pol der ihn erzeugenden
Spannungsquelle fließt), erfahren eine Lorentz-Kraft. Durch Verarmung der Elektronen auf
der einen und Überschuß auf der anderen Seite (bezüglich der Richtung dieser Lorentz-Kraft)
entsteht ein elektrisches Feld EH. Das Feld EH kann durch Abgreifen einer äußeren Spannung
gemessen werden (Hall-Spannung). Aus ihr kann das B-Feld gemessen werden oder bei
bekanntem B die Dichte n der Ladungsträgeranzahl.
Quantitative Betrachtungen:
Lorentzkraft FL = Q [ v × B ] bewirkt seitliche Ablenkung der Ladungsträger:
FL = -e [ v × B] (Q = -e, e: Betrag der Elementarladung).
Nach kurzer Zeit wird FL durch Kraft FE auf Ladungsträger infolge des dann entstandenen
elektrischen Querfeldes EH, FE = - e EH, kompensiert, so daß Gesamtkraft auf jeden
Ladungsträger Null wird:
FL + FE = 0, d.h. e EH = -e [ v × B].
Schreibe nur Beträge und erweitere mit nbd
(n: Dichte der Elektronenanzahl, b: Breite, d: Dicke der Platte)
eEH = eUH /b = e vB = e nbd vB/(nbd)
Das erlaubt den Übergang zu einem Ensemble der Elektronen mit der Stromdichte: j = - env
und mit dem Strom I = jA = j bd = en v bd. Damit folgt:
eEH = I B/(nbd) oder EH = 1/(ne) • I/ (bd) • B ≡ RH • j • B
RH = 1/(ne) : Hall-Koeffizient (für das zugrundeliegende einfache Modell zur Beschreibung
der metallischen Leitfähigkeit!)
Hall-Spannung (zur Spannungsrichtung, vgl. Abbildung):
UH = b EH = RH • I B /d
Hall-Widerstand:
R (Hall) ≡ UH/I = B/(ned) = RH • B/d
Ergänzungen*:
(1) Hall-Effekt bei Halbleitern:
Die Beziehung zur Hall-Konstanten bleibt in ihrer Struktur richtig, wenn man anstelle von n
die Differenz ne - nl aus den Dichten der Leitungselektronen (e) und der Leitungslöcher (l)
setzt und Korrekturen anbringt, die von der Kristall- und Bänderstruktur herrühren.
(2) Quanten-Hall-Effekt:
Messungen der Hall-Spannung an einem MOSFET (metal-oxide-semiconductor field-effect
transistor) bei tiefen Temperaturen ( 1,8 K) und sehr hohen Magnetfeldern (B = 13,0 T) haben
gezeigt [K. von Klitzing, G. Dorda, and M. Pepper, Phys. Rev. Letters 45 , 494 (1980)], daß
die Hall-Spannung einen stufenförmigen Verlauf mit Plateaus besitzt, für die der HallWiderstand bestimmte diskrete Werte annimmt:
R (Hall) = h /(ν e2), mit ν = 1,2,3,...
RK = h / e2 = 25812,807 Ω, für ν = 1 (von-Klitzing-Widerstand, auch als Definition für die
Einheit Ω)
Es ist auch ein Effekt nachgewiesen worden (an GaAs-AlGaAs-Heteroübergängen), bei dem
ν gebrochene Zahlen annimmt, z. B. ν = 2/3, 2/5, 3/5, 4/5 und 2/7): „fractional quantized Hall
effect“ [D. C. Tsui, H. L. Stoermer, and A.C. Grossard, Phys. Rev. Letters 48, 1559 (1982)]
vgl. z. B. die Monographie:
James William Rohlf, Modern Physics from α to Z0 , John Wiley & Sons, Inc, New York
(usw.), 1994, ISBN 0-471-57270-5, S. 395 f.
Der Feld-Effekt-Transistor: MOSFET
(Rohlf, S.393, Fig. 14-24, b,)
D.Michel
Vorlesung Experimentalphysik 2003/04,
Teil 3: Elektrizitätslehre
3.5. Magnetfeld der Erde
(1)
Der magnetische Südpol liegt in der Nähe des geographischen Nordpols (z. Zt. bei
74o nördlicher Breite und 100o westlicher Länge). Der magnetische Nordpol liegt in der
Nähe des geographischen Südpols (z. Zt. bei 72o südlicher Breite und 155o östlicher Länge).
(2)
Die magnetischen Pole wandern statistisch um die geographischen Pole der Erde
herum. Schwankungen des Magnetfeldes in geologischen Zeiträumen: Das Magnetfeld der
Erde kann sich statistisch in unregelmäßigen Abständen auch „umpolen“, im Mittel besteht
eine gleiche Orientierung ca. 2 • 105 Jahre. Nachweisbar durch Messung der Magnetisierung
von eisenhaltigen Gesteinen, die sie bei der Erstarrung bzw. Ablagerung (vor allem
Messungen von Proben von Ozeanböden) im damaligen Magnetfeld der Erde erhalten haben.
Dabei
auch
Bestätigung
der
Theorie
der
Plattentektonik
(Theorie
der
Kontinentalverschiebung, begründet durch Alfred Wegener, 1912)
Eine frei bewegliche Magnetnadel stellt sich in Richtung der Feldlinien des Erdmagnetfeldes
ein. Diese Richtung weist sowohl von der Horizontalen auf Erdoberfläche ab (Inklination) als
auch von Nord-Süd-Richtung (Deklination):
Deklination: declinatio (lat.) = Abweichung, Abweichung von der geographischen Nord-SüdRichtung, im Westen D. etwa 90 und im Osten D. etwa 20, ändert sich mit der Zeit
Inklination: inclinatio (lat.) = Neigung, Abweichung von der Horizontalen, Inklination in
Deutschland zwischen 690 (im Norden D.) und 630 (im Süden D.)
Also: Magnetischer Süd- und Nordpol: Stellen auf Erdoberfläche mit jeweils 90o Inklination
(3)
Eine nur in waagerechter Ebene drehbare Magnetnadel (Kompaßnadel) erfährt allein
die Wirkung der Horizontalkomponente des Erdmagnetfeldes (Horizontalprojektion des
Feldes.
Magnetische Meridiane (Abb. 109, S. 94, aus Grimsehl, Bd. II)
(4)
Das Erdmagnetfeld ist näherungsweise das eines magnetischen Dipols nahe dem
Erdmittelpunkt, dessen Dipolachse um 11,4o gegen die Achse der Erdrotation geneigt ist.
Regionale Anomalien beruhen auf Unregelmäßigkeiten im Strömungssystem des Erdinneren.
Sie lassen sich durch schwache zusätzliche Magnetpole beschreiben (z. B. in Südpol in
Sinkiang, weiterer Zusatzpol in den USA. Dies hat bereits Columbus bei der Entdeckung
Amerikas verwirrt).
Lokale Abweichungen vom idealen Dipolfeld werden durch ungleichmäßige Verteilung
magnetischer Materialien in der Erdkruste bewirkt, z.B. zeigt in Kiruna (Schweden) und in
Kursk (Russland) die Kompaß- Magnetnadel nach Süden.
In größerem Abstand von der Erdoberfläche entstehen Abweichungen vom Dipolfeld durch
Ströme geladener Teilchen (Protonen, Elektronen), die von Sonne emittiert werden
(„Sonnenwind“).
Abb. 3.55 Erdmagnetfeld. Die Quellen des Feldes liegen im
inneren Teil der Erde, die äußeren Schichten tragen kaum
dazu bei. Die Durchstoßpunkte PN, PS der Dipolachse durch
die Erdoberfläche heißen geomagnetische Pole.
(Abb. 3.55, S. 111, aus Demtröder, Bd. II))
(5)
Messungen:
Deklinatorium: Richtung der Horizontalprojektion
(Abb. 108 aus Grimsehl Bd. II)
Systematische Messungen der Horizontalintensität durch Gauss
Inklinatorium: Messung des Inklinationswinkels i, Totalintensitätsmessung mit Hilfe der
Horizontalintensität und mit dem Inklinationswinkel: Btotal = Bhorizontal • sin i
Anwendung in Geophysik: Vorkommen von Eisenerz, z. B. Untersuchung der Anomalie von
Kursk (Russland).
Inklinatorium
(Abb. 111 und 112 aus Grimsehl II)
Komponenten des Erdmagnetismus
d = Deklinationswinkel
i = Inklinationswinkel
(Abb. 112 aus Grimsehl Bd. II)
D.Michel
Vorlesung Experimentalphysik 2003/04,
Teil 3: Elektrizitätslehre
3.6. Magnetfeldmessungen
(1)
Messung durch Überlagerung von Feldern. Tangentenbussole (kein Versuch)
Das magnetische Feld eines Kreisstromes wird dem zu messenden Magnetfeld überlagert
(Erdmagnetfeldmessung). Eine im Mittelpunkt des Kreisleiters stellt sich entlang der
Resultierenden der beiden sich überlagernden Felder ein. Ursprünglich diente diese
Anordnung umgekehrt zum Messen starker Ströme.
Vertikaler Kreis aus Cu-Draht mit Radius r, in dessen Mittelpunkt eine kurze Magnetnadel
über einer Kreisteilung steht. Ebene des Kreistromes wird so eingestellt, daß die ErdfeldHorizontalkomponente HErde in dieser Ebene liegt. Nach Einschalten des Stromes stellt sich
die Magnetnadel in einem bestimmten Winkel α quer ein (α = 0 entspricht Richtung der
Flächennormalen):
tan α = HErde / HStrom
(2)
Modellversuch nach Oersted (Christian Oersted, dänischer Physiker, 1777-1851)
Langer stromdurchflossener Draht, Magnetfeld des langen Drahtes im Abstand r unter dem
Draht und Horizontalkomponente des Erdfeld HE(rde) überlagern, Nachweis des resultierenden
Feldes durch Ablenkung einer kleinen (!) Magnetnadel
(3)
Schwingungsmethode zur Magnetfeldmessung
Drehmoment T = m × B, | T | = mB sinϕ, auf ein magnetisches Moment m im Magnetfeld B,
bewirkt wie bei physikalischem Pendel ein rücktreibendes Moment:
⇒
⇒
⇒
θ d2ϕ/dt2 = - mB sinϕ
harmonische Näherung der Schwingungsgleichung: θ d2ϕ/dt2 = - mB ϕ, falls ϕ << 1
Kreisfrequenz ω, Schwingungsdauer T:
ω2 = mB/θ = (2π/T)2, θ Trägheitsmoment, ϕ kleiner Auslenkwinkel aus der Ruhelage
Messungen
a)
Schwingungsdauer T1 bei Überlagerung von BE(rde) mit parallelem Zusatzfeld BZ:
B = BE + BZ
b)
Schwingungsdauer T2 bei Messung im Erdfeld BE(rde) ohne Zusatzfeld:
B = BE
( BE + BZ ) / BE = T22 / T12 ⇒ BE = BZ ∗ 1/(T22/T12 – 1)
(4)
Erdfeldmessungen nach Gauss (Gauss´sche Hauptlagen)
a)
Ausgangspunkt:
r
r
Analoger Ausdruck des Magnetfeldes H( r ) von magnetischem Dipolmoment m wie
r
elektrisches Feld eines Dipols p E :
rr r
r
r
r
3(mr )r
m
1
H (r ) =
B(r ) =
µ0
r3
r5
b)
r
Verwende Stabmagnet der Länge l mit magnetischem Dipolmoment m sowie
r
Magnetnadel mit magnetischem Dipolmoment m , beide im Abstand r >> 1.
c)
Gauss’sche Hauptlage
(i)
(ii)
r
r r
ohne m . m´ orientiert sich entlang BE (Horizontalkomponente)
r
mit m
r
r
r r
B von m im Abstand r, m || r
r
r
2m
B = B = µ0 3
r
r
r
Drehmoment auf m´ von B :
r
r r
r
T = m´× B(r ) = m´⋅ B ⋅ sin 90° − ϕ 1
(
=
µ 0 2m ⋅ m´
cos ϕ 1
r3
r
r
Drehmoment auf m´ von B
r
TE = µ 0 H E ⋅ m´ ⋅ sin ϕ 1
Gleichheit der Beträge:
m
r3
=
tan ϕ 1
HE
2
d)
2. Gauss´sche Hauptlage
r
r
r r
B von m im Abstand r, m ⊥ r
m
B = µ0 3
r
r
r
Drehmoment auf m´ von B :
r
T = m´ ⋅ B ⋅ sin(90°-ϕ2)
=
m ⋅ m´
cos ϕ 2
r3
r
r
Drehmoment auf m´ von BE :
r
T = µ0BE ⋅ m´ ⋅ sinϕ2
Gleichheit der Beträge:
m
r3
=
tan ϕ 2
HE
2
)
e)
Verbindung der Schwingungsmessungen zur Bestimmung des Produktes mBE:
ω A2 =
BE m
θ
µ H ⋅m
= 0 E
θ
(5)
⇔ Vgl. mit Ergebnis aus Ziffer 2 und/oder 3 liefert m und BE.
Hall-Sonde (siehe Hall-Effekt)
(6)
Präzisionsmessungen mit Hilfe der Kernspinresonanz (Kernmagnetische
Resonanz): Die Resonanz-Kreisfrequenz ωo (Larmor-Frequenz) ist gegeben durch: ωo = γB,
γ (gyromagnetisches Verhältnis) ist eine typische Konstante für jeden Kern mit einem von
Null verschiedenem Kernspin (Kern-Eigendrehimpuls)