Elektromagnetismus - HMTC - Halbmikrotechnik Chemie GmbH

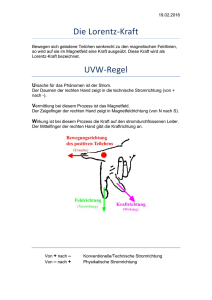
Kartei 309: Lorentz-Kraft und Hall-Effekt
309a
Lorentz-Kraft
Lernkartei
08.04.17
Leite die Lorentz-Kraft formelmäßig aus der
magnetischen Induktion für ein Elektron e ab.
309a
Lorentz-Kraft
08.04.17
F
; (1a) F  B * I * l ;
I * l
(2) I = Q /t;
(1) B

(3) Q
= z*e; (3 in 2 2a) I = z*e /t;
z *e
* l ;
t
den Quotienten v  l / t
(2a in 1a 1b)
F  B*
Bildet man
(Driftgeschwindigkeit der Ladungsträger), so wird aus
(1b 1c) F  B * z * e * v ; die Lorentz-Kraft auf
einen Ladungsträger ist dann FL =F/z;
(1d)
FL  e * v * B
Elektronen bewegen sich entgegen der technische
Stromrichtung von minus nach plus? Wie wirkt sich
das auf die „Rechte-Hand-Regel“ aus?
Dadurch, dass sich die Stromrichtung gegenüber der
technischen Stromrichtung ändert, würde die
„Rechte-Hand-Regel“ eine falsche Kraftrichtung
anzeigen. Man spricht daher von
„Elektronenstromrichtung“ und benutzt dafür die
„Linke-Hand-Regel“.
Die Einheit der magnetischen Induktion ist 1 Tesla.
Drücken Sie die Einheit mit den Einheiten der
Basisgrößen aus
B
Zeigen Sie durch eine Anwendung der
physikalischen Gesetze, dass die Einheit 1 Tesla
auch als 1 V *s / m2 ist.
Über den Energie-Erhaltungssatz kann man die
mechanische Einheit Newton in eine elektrische
Einheit transformieren: Es gilt:
F * s = U * I * t; N*m= V*A*s
Somit ist:N = V*A*s/m ;
1N/(A*m) = (V * A * s / m) / (A * m)  V * s / m2
309b
Hall-Effekt
08.04.17
F
I *l
; daraus folgt 1Tesla ist 1N/(A*m)
309b
08.04.17
Hall-Effekt
Was versteht man unter dem Hall-Effekt?
Leitet man einen elektrischen Strom durch eine
dünne leitende Folie, die sich in ein Magnetfeld
senkrecht zur Stromrichtung befindet, so werden die
Elektronen nach der „Linken-Hand-Regel“ zu einer
Kante hin abgelenkt. Dadurch nimmt die Ladung an
einer Kante zu, an der gegenüberliegenden Kante ab.
Es entsteht quer zum elektrischen Strom ein
elektrisches Feld.
Welche Wirkung hat der Hall-Effekt auf eine dünne
leitende Folie?
Senkrecht zur Stromrichtung und zur senkrecht zur
Magnetfeldrichtung einsteht ein Ladungsunterschied
in der dünnen Folie. Dieser Ladungsunterschied
erzeugt ein homogenes elektrisches Feld E wie bei
einem Plattenkondensator. Die durch das homogene
elektrische Feld E hervorgerufene Spannung UH
hängt mit der Breite b des Folienstreifens nach
E = UH / b zusammen.
Leiten Sie die Hall-Spannung UH aus dem
Kräftegleichgewicht der Lorentz-Kraft mit der
elektrostatischen Kraft ab.
Im Gleichgewicht gilt (1)
(2)
FL  Fel ;
FL  e * v * B und (3) FL  e *U H / b ;
(2&3 in 1 1a) e * v * B  e *U H / b .
(1b)
U H  b * v * B . Um die Driftgeschwindigkeit v
zu ersetzen, benötigt man die Teilchendichte n der
Elektronen, die sich in der Zeit t im Volumen V
bewegen. Es gilt
I  Q / t  nVe / t  nbdle / t  nbdev 
(4) v  I /(nbde) . (4 in 1b1c) U  b * I
H
nbde
(1d)
Was versteht man unter der Hall-Konstante?
UH 
*B ;
1 I *B .
*
ne
d
Den Faktor AH= 1/ne nennt man Hall-Konstante.
© 2005 HMTC Halbmikrotechnik Chemie GmbH; Lernkartei
Letzte Änderung 14.03.2007