Magnetfelder und Lorentzkraft

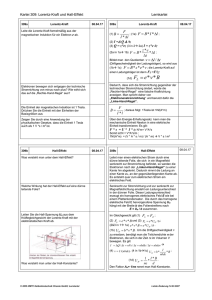
Abiturwiederholung
Physik
Magnetfelder und Lorentz-Kraft
Magnetfelder & magnetische Flussdichte
a. Jeder stromdurchflossene Leiter erzeugt ein Magnetfeld, die Richtung dieses
Magnetfeldes hängt von der Fließrichtung des Stromes ab. Wenn man von der
physikalischen Stromrichtung ausgeht, dann gilt folgende Regel:
„Wenn der Daumen der linken Hand in Richtung des Stromflusses zeigt, dann zeigen die
gekrümmten Finger in Richtung des Magnetfeldes (von N nach S).“
b. Auf jeden Stromdurchflossenen Leiter in einem Magnetfeld, der nicht parallel zu den
Feldlinien steht, wirkt eine Kraft, die wiederum senkrecht auf den beiden Anderen
Größen steht. (siehe Lorentz-Kraft)
c. Anhand von Versuchen kann man feststellen, dass die Kraft abhängig von der
Stromstärke des Stromdurchflossenen Leiters, sowie von der Länge des Leiters ist.
und
, also
, zusammengefasst:
Sofern der Stromdurchflossene Leiter Senkrecht zu den Feldlinien steht gilt:
Ansonsten gilt:
B ist die magnetische Flussdichte, sie hat die Einheit Tesla
Die Lorentz-Kraft
a. Die Lorentz-Kraft wirkt auf einzelne bewegte Ladungsträger im Magnetfeld,
beispielsweise einen Stromdurchflossenen Leiter.
Wenn man davon ausgeht, dass der Strom konstant ist, dann gilt:
Außerdem gilt:
Wenn man diese beiden Bedingungen mit der Beziehung zur Flussdichte verknüpft, so
erhält man folgendes:
Der allgemeine Fall lautet:
b. Die Richtung der Lorentz-Kraft lässt sich über die linke-Hand-Regel bestimmen. Wenn
der Daumen in die Fließrichtung der Elektronen zeigt und der Zeigefinger in Richtung
des Magnetfeldes (N nach S), dann zeigt der Mittelfinger in die Wirkrichtung der
Lorentz-Kraft.
Mark Kremer
-1-
Abiturwiederholung
Physik
c. es ergeben sich folgende Bedingungen für die Bewegung von Teilchen im B-Feld.
I. Wenn sich die Teilchen parallel zu den Feldlinien des magnetischen Feldes
bewegen, dann ist die Lorentz-Kraft null.
II. Bei senkrechtem Eintritt wirkt die Lorentz-Kraft als Radialkraft und die geladenen
Teilchen bewegen sich auf kreisförmigen Bahnen.
III.
Bei schrägem Eintritt in das Magnetfeld, wirkt ebenfalls die Lorentz-Kraft,
allerdings hat man nun zwei Raumrichtungen in die eine Geschwindigkeit wirkt.
Es wirkt zwar noch die Lorentz-Kraft mit dem Betrag
, wobei v
aber nur die Geschwindigkeitskomponente senkrecht zu den Feldlinien ist, durch
die Geschwindigkeitskomponente parallel zu den Feldlinien, wird die Kreisbahn
auseinandergezogen und eine spiralförmige Bahnkurve entsteht.
Magnetische Feldstärke
a. Maß für die Stärke des Magnetfeldes
Wobei:
,
magnetische Feldkonstante,
Permeablitätszahl
Magnetfeld der elektrischen Spule
Eine Spule ist quasi ein sehr langer stromdurchflossener Leiter, um die magnetische Feldstärke
oder Flussdichte zu bestimmen muss man also auch die Anzahl der Windungen betrachten,
genauso wie die mittlere Feldlinienlänge, die von den geometrischen Abmessungen der Spule
abhängt.
Stromstaerke( I )  Windungen ( N )
Magnetisch e  Feldstaerk eH  
mittlereFe ldlinienla enge(l )
Die mittlere Feldlinienlänge wird berechnet indem:
  (d a  d i )
lm 
2
Dabei kann l aber auch durch lsp ersetzt werden, der Länge der Spule.
Anwendung
Wenn man die obigen Beziehungen Anwendet, ergeben sich Methoden zur:
Bestimmung von
a. Man macht sich die zweite Bedingung der Lorentz-Kraft (siehe Lorentz-Kraft/c/II) zu
Nutze und zwingt das Teilchen auf eine Kreisbahn.
b. Aufbau:
Man erzeugt freie Elektronen mit Hilfe einer
Glühkatode, diese werden beschleunigt durch eine
Beschleunigungsspannung (Anodenspannung) und
senkrecht in ein homogenes Magnetfeld geschossen.
Mark Kremer
-2-
aus "Abitur Physik, Basiswissen
Schule“, DUDEN
Abiturwiederholung
Physik
c. Durch die Beschleunigungsspannung haben die Elektronen eine Geschwindigkeit von
Die Lorentz-Kraft wirkt als Radialkraft:
Durch Einsetzen der Geschwindigkeit:
Somit ist
von konstanten Größen abhängig.
Hall Effekt
a. Da Ladung auch im Stromdurchflossenen Leiter durch ein Magnetfeld beeinflusst wird,
kann man sich diese Gegebenheit zunutze machen um das B-Feld zu bestimmen.
b. Aufbau:
Ein Stromdurchflossener Leiter wird senkrecht zur
Driftgeschwindigkeit der Elektronen in ein
Magnetfeld gesetzt. Man misst die Spannung
zwischen den Punkten A und B.
c. Die Elektronen werden soweit durch die LorentzKraft abgelenkt, bis die Kraft durch das elektrische
aus "Abitur Physik, Basiswissen
Feld so groß wird, dass es zum Kräftegleichgewicht Schule“, DUDEN
kommt.
wobei h die Höhe des Leiterstückes ist
Die Driftgeschwindigkeit hängt von der Stromstärke ab
Da sich in dem Leiterstück nur eine gewisse Menge Elektronen aufhalten, gilt:
, also
Die Ladungsdichte c, ist definiert:
(wobei V das Volumen ist)
, somit ist
Da Weg durch Zeit immer eine Geschwindigkeit ist, kann man
Wenn man alles zusammensetzt erhält man folgenden Term:
Mark Kremer
-3-
durch v ersetzen.
Abiturwiederholung
Physik
Wobei RH die Hallkonstante ist.
Stromwaage
a. Die Stromwage ist quasi der Grundlagen-Versuch um die magnetische Feldstärke zu
beschreiben
b. Man hält eine Leiterschleife senkrecht in ein Magnetfeld und misst die Kraft die darauf
wirkt, bzw. bestimmt die Abhängigkeit von Kraft zu Länge der Leiterschleife und von
Kraft zu Stromstärke.
Massenspektrograph
a. Es gibt zwei Varianten, die auf dem gleichen System basieren, beide benutzen die
Kombination von E- und B-Feld um Stoffe nach ihren spezifischen Massen zu ordnen.
Es gibt die Variante von Thomson und von Aston
b. Der Massenspektrograph von Thomson basiert auf einer Ionenquelle, welche Ionen mit
verschiedenen Geschwindigkeiten in ein Magnetfeld und in ein elektrisches Feld, auf
gleicher Ebene, schleudert.
Die Teilchen werden Abgelenkt und landen auf einer Fotoplatte und bilden eine Parabel.
c. Mathematische Beschreibung:
Zum einen betrachtet man die Geschwindigkeit
über die Länge des Kondensators.
L  v0  t , außerdem gilt in y-Richtung eine
beschleunigte Bewegung.
y  0.5a  t 2 .
a kann über die Beziehung m  a  Q  E
beschrieben werden. Nun kann man t eliminieren
und nach y auflösen, dann ergibt sich:
Q  E  L2
y
2  m  v02
Nun kann man ebenfalls die Ablenkung durch die
Lorentz-Kraft bestimmen mit
ma  Qv B
Wenn man wie oben auch auflöst erhält man:
Q  B  L2
x
2  m  v02
wenn man nun beide Terme nimmt um v zu eliminieren, dann kann man aufstellen:
2  E  m  x2
y
. Es zeigt sich, dass wenn E,B und L konstant sind, die Form der
Q  B 2  L2
Parabel lediglich von Q und m abhängig ist.
d. Der Massenspektrograph von Aston umgeht die verschiedenen Geschwindigkeiten,
indem er einen Geschwindigkeitsfilter einbaut
Mark Kremer
-4-
Abiturwiederholung
Physik
e. Ein Ionenstrahl durchquert ein Magnetfeld und
ein senkrecht dazu angeordnetes elektrisches
Feld, gleichzeitig.
Damit die Ionen geradeaus fliegen, müssen sich
die Kräfte kompensieren.
Es gilt somit, dass
FL  Fel
FL  Q  v  B
Fel  Q  E
Qv B  Q E
E
v
B
Durch diese Anordnung ist garantiert, dass nur Teilchen gleicher Geschwindigkeit das
Feld verlassen. Man dies auch den Wien-Filter.
f. Die Ionen gelangen in ein weiteres Magnetfeld, wo sie abgelenkt werden. Es gilt wie
beim Fadenstrahlrohr, dass die Zentripetalkraft gleich der Lorentz-Kraft sein muss.
Fz  FL
m  v2
r
FL  Q  v  B
Das heißt:
m  v2
Qv B 
r
durch Umformungen:
Q
v

m rB
Die Geschwindigkeit v kann man weiterhin von der Anodenspannung abhängig machen,
da die Ionen die Felder nur durchqueren (d.h. nicht noch mal abgelenkt werden)
Aufgrund des Energieerhaltungssatzes gilt:
Q
v  2 Ua
m
Nun ergibt sich:
Fz 
Q 2U a

m B2r 2
Da U und B Konstant sind, ist die Kreisbahn nur von Q und m abhängig.
Mark Kremer
-5-