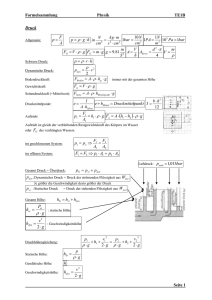
Zinseszinsrechnung

Formelsammlung für Handelsakademie
Zinseszinsrechnung
1
-->
Endkapital
K[n]=K[0]*r**n;
(%o1) Kn = K0 rn
Aufzinsungsfaktor
-->
r=1+p/100;
(%o2) r =
-->
p
+1
100
r=1+i;
(%o3) r = i + 1
2
-->
Anfangskapital
K[0]=K[n]/r**n;
(%o4) K0 =
3
-->
Zinssatz
r=(K[n]/K[0])**(1/n);
(%o5) r =
-->
Kn
rn
Kn
K0
n1
p=100*(r-1);
(%o6) p = 100 (r − 1)
1
07/10/2013
Johann Weilharter
Seite 1 von 23
Formelsammlung für Handelsakademie
4
-->
Laufzeit
n=(log(K[n])-log(K[0]))/log(r);
(%o7) n =
log (Kn ) − log (K0 )
log (r)
2
07/10/2013
Johann Weilharter
Seite 2 von 23
Formelsammlung für Handelsakademie
Rentenrechnung
1
-->
Endwert der nachschüssigen Rente
E=(r**n-1)*R/i;
(%o8) E =
2
-->
Barwert der nachschüssigen Rente
B=R*(1-v**n)/i;
(%o9) B =
3
-->
(rn − 1) R
i
(1 − v n ) R
i
Endwert der vorschüssigen Rente
E = R*((r**n-1)/d);
(rn − 1) R
d
d ist der Diskontsatz, d = i/(1+i)
(%o10) E =
4
-->
Barwert der vorschüssigen Rente
B=R*(1-v**n)/d;
(%o11) B =
5
(1 − v n ) R
d
Äquivalenzprinzip
ÄQUIVALENZPRINZIP
Das ist das Grundprinzip von Geldgeschäften:
Leistung = Gegenleistung (bezogen auf denselben Zeitpunkt)
3
07/10/2013
Johann Weilharter
Seite 3 von 23
Formelsammlung für Handelsakademie
ANWENDUNGEN
* Rentenumwandlung
* Investitionsrechnung
* Tilgungsplan
-->
kill(all);
(%o0) done
4
07/10/2013
Johann Weilharter
Seite 4 von 23
Formelsammlung für Handelsakademie
Kosten- und Preistheorie
1
Lineare Kostenfunktion
Die lineare Kostenfunktion ist ein sehr einfaches Modell. K = Gesamtkosten k
= proportionale Kosten k*x = variable Kosten F = Fixkosten
-->
K(x):=k*x+F;
(%o1) K (x) := k x + F
Bei einer linearen Kostenfunktion gibt es kein -> Betriebsoptimum!
2
-->
Quadratische Kostenfunktion
K(x):=a*x**2+b*x+c;
(%o2) K (x) := a x2 + b x + c
c sind die Fixkosten
3
-->
Kubische Kostenfunktion
K(x):=a*x**3+b*x**2+c*x+d;
(%o3) K (x) := a x3 + b x2 + c x + d
d sind die Fixkosten Eine geeignete Kostenfunktion dritten Grades gibt eine
s-förmige Kostenkurve
-->
kill(all);
(%o0) done
4
Betriebsoptimum
Das Betriebsoptimum ist jene Ausbringungsmenge, bei der die Durch- schnittskosten
am kleinsten werden. Die kleinsten Durchschnitts- kosten heißen auch langfristige
Preisuntergrenze. Die Durchschnitts- kosten nennt man auch Stückkosten. Die
Berechnung des Betriebsoptimums ist eine Extremwertaufgabe Allgemein für
Kostenfunktion
5
07/10/2013
Johann Weilharter
Seite 5 von 23
Formelsammlung für Handelsakademie
-->
K(x);
(%o1) K (x)
Allgemein für Durchschnittskosten
-->
DK(x):=K(x)/x;
K (x)
x
Wir müssen die erste Ableitung NULL setzen, das ist die notwendige Bedingung
für das Auftreten eines Extremwerts!
(%o2) DK (x) :=
-->
ab:diff(DK(x),x);
(%o3)
K (x) ddx
K (x)
−
x
x2
-->
l:solve(ab=0);
(%o4) [x =
K (x)
]
K (x) ddx
Das ist die allgemeine Lösung für das Betriebsoptimum: Grenzkosten = Durchschnittskosten
5
Minimum der Durchschnittskosten = langfristige
Preisuntergrenze
Wenn man das Betriebsoptimum in die Durchschnittskosten einsetzt, erhält
man das Minimum der Durchschnittskosten. Dieses nennt man auch langfristige
Preisuntergrenze.
6
Grenzkosten
Die Grenzkosten geben an, wie sich die Kosten ändern, wenn sich die Ausbringungsmenge im Durchschnitt um EINS ändert.
Die Grenzkosten sind die Ableitung der Gesamtkosten.
-->
K(x);
(%o5) K (x)
6
07/10/2013
Johann Weilharter
Seite 6 von 23
Formelsammlung für Handelsakademie
-->
GK(x):=’diff(K(x),x);
(%o6) GK (x) := K (x)
7
d
dx
Kostenkehre
Die Kostenkehre, ist der Wendepunkt der Kostenkurve. In der Kostenkehre
haben die Grenzkosten ein Minimum. Kostenfunktion
-->
K(x);
(%o7) K (x)
Man muss die zweite Ableitung der Kostenfunktion NULL setzen
-->
ab2:’diff(K(x),x,2);
(%o8)
K (x)
-->
l:solve(ab2=0,x);
(%o9) [ K (x)
8
d2
d x2
d2
= 0]
d x2
Definition: Nachfrage
Die Nachfrage gibt an, wie sich die nachgefragte Menge ändert, wenn sich der
Preis ändert.
9
Normales Nachfragegesetz
wenn der Preis steigt, sinkt die Nachfrage und umgekehrt wenn der Preis sinkt,
steigt die Nachfrage
Eine bekannte Ausnahme ist der Snob-Effekt (”was nichts kostet, ist nichts
wert”)
10
-->
Lineare Nachfragefunktion
p(x):=a*x+b;
(%o10) p (x) := a x + b
7
07/10/2013
Johann Weilharter
Seite 7 von 23
Formelsammlung für Handelsakademie
11
-->
Quadratische Nachfragefunktion
p(x):=a*x**2+b*x+c;
(%o11) p (x) := a x2 + b x + c
Berechnungen
* lineare Funktion aus zwei Punkten * lineare Funktion aus mehr als zwei Punkten -> lineare Regression * quadratische Funktion aus drei Punkten
12
Definition: Umsatz
Der Umsatz (auch ”Erlös”) ist das Produkt aus Menge x Preis
Das darf man nicht mit dem mengenmäßigen Umsatz, den man auch Absatz (
oder auch -> Nachfrage nennt)
-->
U(x):=p(x)*x;
(%o12) U (x) := p (x) x
13
-->
Umsatz bei linearer Nachfragefunktion
p(x):=a*x+b;
(%o13) p (x) := a x + b
-->
U(x):=p(x)*x;
(%o14) U (x) := p (x) x
-->
U(x);
(%o15) x (a x + b)
-->
expand(%);
(%o16) a x2 + b x
Ergebnis: wenn eine lineare Nachfragefunktion gegeben ist, dann ist die Umsatzfunktion eine quadratische Funktion
8
07/10/2013
Johann Weilharter
Seite 8 von 23
Formelsammlung für Handelsakademie
14
-->
Umsatz bei quadratischer Nachfragefunktion
p(x):=a*x**2+b*x+c;
(%o17) p (x) := a x2 + b x + c
-->
U(x):=p(x)*x;
(%o18) U (x) := p (x) x
-->
U(x);
(%o19) x a x2 + b x + c
-->
expand(%);
(%o20) a x3 + b x2 + c x
Bei einer quadratischen Nachfragefunktion ergibt sich eine Umsatzfunktion dritten Grades.
-->
kill(all);
(%o0) done
15
-->
Umsatzmaximale Menge
p(x);
(%o1) p (x)
-->
U(x):=p(x)*x;
(%o2) U (x) := p (x) x
Man muss die erste Ableitung bestimmen
-->
ab:diff(U(x),x);
d
(%o3) x p (x)
+ p (x)
dx
Wenn man diese Ableitung NULL setzt, erhält man die umsatzmaximale Menge.
9
07/10/2013
Johann Weilharter
Seite 9 von 23
Formelsammlung für Handelsakademie
16
Umsatzmaximaler Preis
Wenn man die umsatzmaximale Menge in die Nachfrage- funktion einsetzt,
erhält man den umsatzmaximalen Preis.
17
Maximaler Umsatz
Wenn man die umsatzmaximale Menge in die Umsatz- funktion einsetzt, dann
erhält man den maximalen Umsatz.
18
Defintion: Gewinn
Gewinn = Erlös - Kosten Gewinn = Umsatz - Kosten
-->
G(x):=E(x)-K(x);
(%o4) G (x) := E (x) − K (x)
-->
G(x):=U(x)-K(x);
(%o5) G (x) := U (x) − K (x)
19
Gewinn
-->
G(x) > 0;
(%o6) x p (x) − K (x) > 0
20
-->
Weder Gewinn noch Verlust
G(x)= 0;
(%o7) x p (x) − K (x) = 0
21
Verlust
-->
G(x) < 0;
(%o8) x p (x) − K (x) < 0
10
07/10/2013
Johann Weilharter
Seite 10 von 23
Formelsammlung für Handelsakademie
22
-->
Berechnung der Gewinnzone
G(x) = 0;
(%o9) x p (x) − K (x) = 0
-->
E(x) = K(x);
(%o10) E (x) = K (x)
Untergrenze der Gewinnzone: * Break Even Point * Nutzenschwelle * Gewinnschwelle
Obergrenze der Gewinnzone: * Nutzengrenze * Gewinngrenze
23
Cournotsche Menge
Die Counotsche Menge ist jene Menge, für die der Gewinn maximal wird. Das
ist also die gewinnmaximale Menge.
Wenn man die Cournotsche Menge in die Nachfragefunktion einsetzt, erhält
man den Cournotschen Preis. Der sogenannte Cournotsche Punkt hat zwei
Koordinaten: die Cournotsche Menge xC und den Cournotschen Preis pC.
Wenn man den Cournotschen Preis in den Gewinn einsetzt, erhält man den
maximalen Gewinn.
11
07/10/2013
Johann Weilharter
Seite 11 von 23
Formelsammlung für Handelsakademie
Wahrscheinlichkeitsrechnung
1
Wahrscheinlichkeitsverteilung
-->
n:6;
(%o11) 6
Zufallsvariable
-->
X:makelist(x[i],i,1,n);
(%o12) [x1 , x2 , x3 , x4 , x5 , x6 ]
Absolute Häufigkeiten
-->
H:makelist(h[i],i,1,n);
(%o13) [h1 , h2 , h3 , h4 , h5 , h6 ]
-->
N:sum(h[i],i,1,’n);
(%o14)
n
X
hi
i=1
Relative Häufigkeiten = Wahrscheinlichkeiten
-->
P:H/N;
h1
(%o15) [ Pn
i=1
2
-->
hi
h2
, Pn
i=1
hi
h3
, Pn
i=1
hi
h4
, Pn
i=1
hi
h5
, Pn
i=1
hi
h6
, Pn
i=1
hi
]
Erwartungswert
kill(all);
(%o0) done
-->
E(X)=sum(h[i]*x[i],i,1,n)/sum(h[i],i,1,n);
Pn
i=1 hi xi
(%o1) E (X) = P
n
i=1 hi
12
07/10/2013
Johann Weilharter
Seite 12 von 23
Formelsammlung für Handelsakademie
-->
E(X)=sum(p[i]*x[i],i,1,n);
(%o2) E (X) =
n
X
p i xi
i=1
3
Varianz
-->
V(X) = E((X-m)**2);
2
(%o3) V (X) = E (X − m)
4
Streuung oder Standardabweichung
-->
S(X) = sqrt(V(X));
p
(%o4) S (X) = V (X)
5
Beispiel: Schularbeitenstatistik
Die österreichische Notenskala ist in diesem Beispiel die Zufallsvariable X
-->
X:[1,2,3,4,5];
(%o5) [1, 2, 3, 4, 5]
Häufigkeiten: Es gab 2 mal ”Sehr gut” 3 mal ”Gut” 6 mal ”Befriedigend” 4 mal
”Genügend” 5 mal ”Nicht genügend”
-->
H:[2,3,6,4,2];
(%o6) [2, 3, 6, 4, 2]
Die Länge der Liste bestimmen als Obergrenze für den Summationsindex
-->
n:length(H);
(%o7) 5
-->
N:sum(H[i],i,1,n);
(%o8) 17
13
07/10/2013
Johann Weilharter
Seite 13 von 23
Formelsammlung für Handelsakademie
-->
P:H/N;
(%o9) [
6
2 3 6 4 2
, , , , ]
17 17 17 17 17
Der Erwartungswert
-->
m:sum(P[i]*X[i],i,1,n);
(%o10)
52
17
-->
X1:(X-m)**2;
(%o11) [
7
1225 324 1 256 1089
,
,
,
,
]
289 289 289 289 289
Die Varianz
-->
v:sum(P[i]*X1[i],i,1,n);
(%o12)
390
289
8
Die Streuung (Standardabweichung)
-->
s:sqrt(v);
√
390
(%o13)
17
9
-->
Additionssatz
"W(A oder B) = W(A) + W(B)";
(%o14) W (AoderB) = W (A) + W (B)
14
07/10/2013
Johann Weilharter
Seite 14 von 23
Formelsammlung für Handelsakademie
10
-->
(%o15)
Additionssatz auf eine Verteilung angewendet
’sum(W(x[k]),k,1,’n)=1;
n
X
W (xk ) = 1
k=1
11
Kumulierte Verteilung
-->
W(x<=k)=’sum(W(x[i]),i,1,k);
(%o16) W (x <= k) =
k
X
W (xi )
i=1
-->
kill(all);
(%o0) done
15
07/10/2013
Johann Weilharter
Seite 15 von 23
Formelsammlung für Handelsakademie
Wahrscheinlichkeitsverteilungen
1
Binomialverteilung
Parameter: n (Umfang der Stichprobe) p (zugrunde liegende Wahrscheinlichkeit)
-->
n;
(%o1) n
-->
p;
(%o2) p
-->
E:n*p;
(%o3) n p
-->
V:n*p*(1-p);
(%o4) n (1 − p) p
-->
W(k):=binomial(n,k)*p**k*(1-p)**(n-k);
n
n−k
(%o5) W (k) :=
pk (1 − p)
k
2
Poissonverteilung
h Parameter: m=E=V
-->
m;
(%o6) m
-->
W(k):=m**k/k!*exp(-m);
(%o7) W (k) :=
mk
exp (−m)
k!
16
07/10/2013
Johann Weilharter
Seite 16 von 23
Formelsammlung für Handelsakademie
3
-->
Komplementärereignis
"W(A’)=1-W(A)";
(%o8) W (A0 ) = 1 − W (A)
-->
kill(all);
(%o0) done
17
07/10/2013
Johann Weilharter
Seite 17 von 23
Formelsammlung für Handelsakademie
Differentialrechnung
1
Potenzregel
-->
f(x):=x**n;
(%o1) f (x) := xn
-->
’diff(f(x),x)=diff(f(x),x);
(%o2) xn
2
d
= n xn−1
dx
Regel vom konstanten Faktor
-->
f(x):=c*u(x);
(%o3) f (x) := c u (x)
-->
(%o4)
3
’diff(f(x),x)=diff(f(x),x);
d
d
(c u (x))
= c u (x)
dx
dx
Summen- und Differenzregel
-->
f(x):=u(x)+v(x);
(%o5) f (x) := u (x) + v (x)
-->
’diff(f(x),x)=diff(f(x),x);
(%o6)
(v (x) + u (x))
4
-->
d
d
d
= v (x)
+ u (x)
dx
dx
dx
Produktregel
f(x):=u(x)*v(x);
(%o7) f (x) := u (x) v (x)
18
07/10/2013
Johann Weilharter
Seite 18 von 23
Formelsammlung für Handelsakademie
-->
(%o8)
5
-->
’diff(f(x),x)=diff(f(x),x);
d
d
d
(u (x) v (x))
= u (x) v (x)
+ v (x) u (x)
dx
dx
dx
Quotientenregel
f(x):=u(x)/v(x);
(%o9) f (x) :=
-->
u (x)
v (x)
’diff(f(x),x)=diff(f(x),x);
u (x) v (x) ddx
u (x) ddx
u (x) d
(%o10)
=
−
2
v (x) d x
v (x)
v (x)
-->
factor(%);
u (x) v (x) ddx − v (x) u (x) ddx
u (x) d
(%o11)
=−
2
v (x) d x
v (x)
19
07/10/2013
Johann Weilharter
Seite 19 von 23
Formelsammlung für Handelsakademie
Integralrechnung
Die Integralrechnung ist die Umkehrung der Differentialrechnung.
1
Das unbestimmte Integral
-->
f(x):=x**2;
(%o12) f (x) := x2
-->
’integrate(f(x),x) = integrate(f(x),x);
Z
x3
(%o13)
x2 dx =
3
2
Das bestimmte Integral
-->
f(x):=x**2;
(%o14) f (x) := x2
-->
a:0;
(%o15) 0
-->
b:1;
(%o16) 1
-->
’integrate(f(x),x,a,b) = integrate(f(x),x,a,b);
Z
(%o17)
1
x2 dx =
0
-->
1
3
kill(all);
(%o0) done
20
07/10/2013
Johann Weilharter
Seite 20 von 23
Formelsammlung für Handelsakademie
Kurvendiskussion
1
Nullstellen
Die Nullstellen einer Funktion sind ihre Schnittpunkte mit der x-Achse
-->
f(x):=(x**2-8*x+15)*x/10;
x2 − 8 x + 15 x
(%o1) f (x) :=
10
-->
solve(f(x)=0);
(%o2) [x = 3, x = 5, x = 0]
-->
realroots(f(x));
(%o3) [x = 3, x = 5, x = 0]
2
Extremwerte
Zuerst die x-Werte durch NULL-Setzen der ersten Ableitung bestimmmen, die
Funktionswerte durch Rückeinsetzen in f(x). Mittels der zweiten Ableitung
kann man dann entscheiden, ob ein Maximum (Hochwert) oder ein Minimum
(Tiefwert) vorliegt.
Wenn die zweite Ableitung < 0 ist, liegt ein Maximum vor, wenn die zweite
Ableitung > 0 ist, liegt ein Minimum vor.
-->
ab:diff(f(x),x);
(%o4)
x2 − 8 x + 15 x (2 x − 8)
+
10
10
-->
solve(ab=0,x);
√
√
19 − 8
19 + 8
(%o5) [x = −
,x =
]
3
3
-->
realroots(ab);
(%o6) [x =
40725025
138231945
,x =
]
33554432
33554432
21
07/10/2013
Johann Weilharter
Seite 21 von 23
Formelsammlung für Handelsakademie
3
Wendepunkte
-->
ab2:diff(f(x),x,2);
(%o7)
2x − 8 x
+
5
5
-->
solve(ab2=0,x);
(%o8) [x =
-->
8
]
3
realroots(ab2);
89478485
]
33554432
Der Hauptzweck der Kurvendiskussion ist die Erstellung einer grafischen Darstellung. Dazu gibt es allerdings heute sehr gut geeignete Programme.
(%o9) [x =
22
07/10/2013
Johann Weilharter
Seite 22 von 23
Formelsammlung für Handelsakademie
Regressionsrechnung
1
Lineare Regression
Hier sind die zwei Gleichungen, die man für eine lineare Regression braucht:
-->
a*sum(x[i]**2,i,1,n)+b*sum(x[i],i,1,n)=sum(x[i]*y[i],i,1,n);
!
n
n
n
X
X
X
2
(%o10) a
xi + b
xi =
xi yi
i=1
-->
i=1
i=1
a*sum(x[i],i,1,n)+b*n = sum(y[i],i,1,n);
(%o11) b n + a
n
X
i=1
xi =
n
X
yi
i=1
Anmerkung: wegen der verfügbaren Summenarithmetik ist Maxima für Regressionsrechnungen ganz besonders gut geeignet.
23
07/10/2013
Johann Weilharter
Seite 23 von 23