1 Konstanten

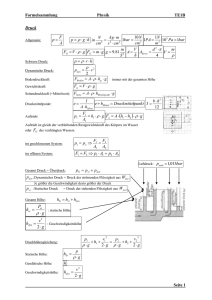
Formelsammlung
1 Konstanten
c = 2, 998 · 108 ms−1
kB = 1, 38 · 10−23 =
R
JK −1
NA
h = 6, 63 · 10−34 Js
me = 9, 109 · 10−31 kg
1eV = 1, 602 · 10−19 J
F = 96485
NA = 6, 0223 · 1023
Physikalische Chemie II
1
Bomze Daniel 0726183
Formelsammlung
2 Formeln
2.1 Reale und ideale Gase
n2 a
nRT
− 2
V − nb
V
Vm
pVm
z = ideal =
RT
Vm
a
TB =
Rb
p=
∫p
f = γ(p, T ) · p = p · e
(
0
)
z−1
′
p
dp
2.2 Thermodynamik
∆G = ∆H − T ∆S
∆G = −RT lnk
(
)
1
∆Hr0 1
−
ln(KT1 ) = ln(KT2 ) −
R
T1 T2
nRT
Π=
V
( )νi
pi
p0
Kp = ( )νj
pj
p0
(
)
pges −∆ν
Kp = Kx ·
p0
pi = xi · pges
2.3 Elektrochemie
0
0
E 0 = EKathode
− EAnode
( 0)
∂E
∆S 0 = zF
∂T p
∆G0 = −zF E
Physikalische Chemie II
2
Bomze Daniel 0726183
Formelsammlung
2.3.1 Nernst-Gleichung
RT
E=E −
· ln
zF
0
2.3.2 Konzentrationszelle
RT
E=
· ln
zF
(
(
aνP rodukte
aνEdukte
aνP rodukte
aνEdukte
)
)
2.4 Photochemie
2.4.1 Quantenausbeute
ϕ=
NumgesetzteM olekuele
NabsorbierteP hotonen
2.4.2 Energie eines Elektrons abzüglich der Austrittsarbeit
E =h·ν−ϕ
Ekin =
m · v2
2
2.5 Ideale und reale Lösungen
ai = xi · γ +
−
pLoesungsmittel
aLoesungsmittel = ∗
pLoesungsmittel
)
m∑ (
2
2
I=
i νi+ zi+
+ νi− zi−
2
√
logγ + = −0.5092|z+ z− | I
−
2.5.1 Henry-Gesetz
Gilt für sehr kleine Konzentrationen
i
pi = xi · kH
2.5.2 Raoult-Gesetz
pi = xi · p∗i
Physikalische Chemie II
3
Bomze Daniel 0726183
Formelsammlung
2.5.3 Gefrierpunktserniedrigung und Siedepunktserhöhung
∆Tf = −Kf · mgeloesterStof f
∆Tb = Kb · mgeloesterStof f
2.6 Quantenmechanik
h
p
p=m·v
λ=
E =h·ν
2.6.1 1-Dimensionaler Potentialtopf
En =
h2 · n2
8 · m · a2
2.6.2 3-Dimensionaler Potentialtopf
h2
En =
8·m
(
n2x n2y
n2z
+
+
a2
b2
c2
)
2.6.3 harmonischer Oszillator
1
Ev = (v + ) · h · ν
2
√
1
k
ν=
·
2π
µ
2.6.4 starrer Rotator
Ej = (j + 1)jhcB
B=
h
8π 2 cI
I = r2 · µ
m1 · m2
µ=
m1 + m2
Physikalische Chemie II
4
Bomze Daniel 0726183
Formelsammlung
2.6.5 Schrödingergleichung
Eindimensionale, Zeitunabhängige SG
−h̄2 d2
Ψ(x) + V (x)Ψ(x) = EΨ(x)
2m dx2
Dreidimensionale, Zeitunabhängige SG
(
)
d2
d2
−h̄2 d2
+
+
Ψ(x, y, z) + V (x, y, z)Ψ(x, y, z) = EΨ(x, y, z)
2m dx2 dz 2 dz 2
Eindimensionale, Zeitababhängige SG
−h̄2 d2
∂Ψ(x, t)
Ψ(x, t) + V (x, t)Ψ(x, t) = ih̄
2m dx2
∂t
2.6.6 Operatoren
p̂x = −ih̄
Êkin = −
∂
∂x
h̄2 ∂ 2
1
(p̂x ) p̂x
=
2
2m ∂x
2m
x̂ = x
Êpot = V (x)
h̄2 ∂ 2
+ V (x)
2m ∂x2
( )
∂z
∂y
−
Îx = −ih̄
∂z
∂y
Ĥ = −
2.7 Heisenbergsche Unschärferelation
∆x >
h̄
h
=
2∆p
4π∆p
2.8 Statistische Thermodynamik
2.8.1 Boltzmann-Verteilung
gj ∆ε
nj
= e− kT
ni
gi
S = kB · ln(W )
Physikalische Chemie II
5
Bomze Daniel 0726183
Formelsammlung
2.8.2 Zustandssummen
V
Λ3
h
Λ= √
2πmkT
1
qV =
∆E
1 − e− kT
qT =
2.8.3 molare Wärmekapazität
Cv = (Cv )T + (Cv )R + (Cv )V ib
(Cv )Rot
3
(Cv )T rans = R
2
lineare M olekuele : (Cv )R = R
3
(Cv )Rot gewinkelte M olekuele : (Cv )R = R
2
(
)
∂U
cv =
∂T V
R
e− kT
2
=
∆E
(
)
∆E 2
(kT )2
1 − e− kt
∆E
(Cv )V ib
Cp = Cv + R
Physikalische Chemie II
6
Bomze Daniel 0726183