Die gleichförmige Bewegung - minus-p
Werbung
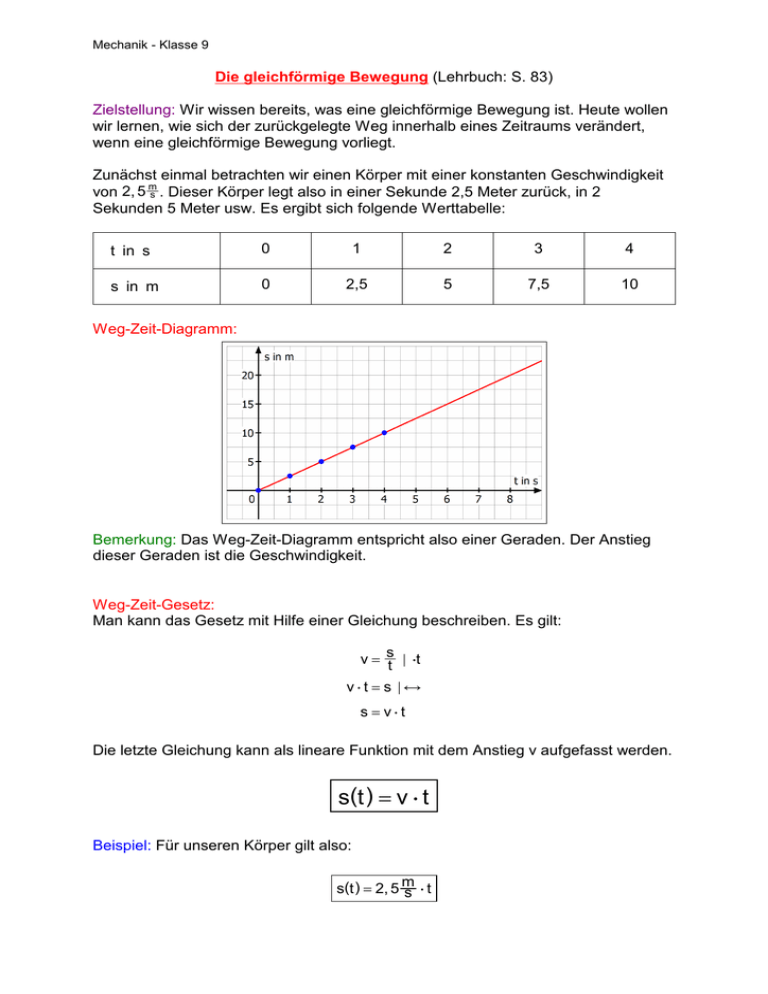
Mechanik - Klasse 9 Die gleichförmige Bewegung (Lehrbuch: S. 83) Zielstellung: Wir wissen bereits, was eine gleichförmige Bewegung ist. Heute wollen wir lernen, wie sich der zurückgelegte Weg innerhalb eines Zeitraums verändert, wenn eine gleichförmige Bewegung vorliegt. Zunächst einmal betrachten wir einen Körper mit einer konstanten Geschwindigkeit von 2, 5 ms . Dieser Körper legt also in einer Sekunde 2,5 Meter zurück, in 2 Sekunden 5 Meter usw. Es ergibt sich folgende Werttabelle: t in s 0 1 2 3 4 s in m 0 2,5 5 7,5 10 Weg-Zeit-Diagramm: Bemerkung: Das Weg-Zeit-Diagramm entspricht also einer Geraden. Der Anstieg dieser Geraden ist die Geschwindigkeit. Weg-Zeit-Gesetz: Man kann das Gesetz mit Hilfe einer Gleichung beschreiben. Es gilt: v = st x $t v $ t = s xv s = v$t Die letzte Gleichung kann als lineare Funktion mit dem Anstieg v aufgefasst werden. s( t ) = v $ t Beispiel: Für unseren Körper gilt also: s(t ) = 2, 5 m s $t Mechanik - Klasse 9 Geschwindigkeit-Zeit-Diagramm: Da die Geschwindigkeit bei der gleichförmigen Bewegung konstant ist, ergibt sich eine parallele Gerade zur x-Achse. Geschwindigkeit-Zeit-Gesetz: v(t ) = konst. Beispiel: Für unseren Körper gilt also: v(t ) = 2, 5 m s Aufgaben: 1. Ein Radfahrer fährt 20 min mit einer Geschwindigkeit von 18 km h . a) Stellen Sie das Weg-Zeit-Gesetz auf. Verwenden Sie die Grundeinheiten. b) Stellen Sie das Weg-Zeit-Gesetz graphisch dar. c) Berechnen Sie, welche Strecke der Radfahrer nach 17 min zurückgelegt hat. 2. Gegeben ist ein Weg-Zeit-Diagramm a) Berechnen Sie die Geschwindigkeit in den beiden Abschnitten. b) Zeichnen Sie das dazugehörige Geschwindigkeit-Zeit-Diagramm. c)* Berechnen Sie die Durchschnittsgeschwindigkeit. Mechanik - Klasse 9 Lösungen: 1. Ein Radfahrer fährt 20 min mit einer Geschwindigkeit von 18 km h . a) Stellen Sie das Weg-Zeit-Gesetz auf. Verwenden Sie die Grundeinheiten. v = 5 ms u s(t ) = 5 ms $ t b) Stellen Sie das Weg-Zeit-Gesetz graphisch dar. c) Berechnen Sie, welche Strecke der Radfahrer nach 17 min zurückgelegt hat. t = 17 min = 1020s s(1020s ) = 5 m s $ 1020s = 5100m = 5, 1km Das Radfahrer hat 5,1 km zurückgelegt. 2. Gegeben ist ein Weg-Zeit-Diagramm a) Berechnen Sie die Geschwindigkeit in den beiden Abschnitten. v 1 = 150m = 7, 5 m s 20s v 2 = ✁s = 225m − 150m = 75m = 1, 5 m s ✁t 70s − 20s 50s b) Zeichnen Sie das dazugehörige Geschwindigkeit-Zeit-Diagramm. c)* Berechnen Sie die Durchschnittsgeschwindigkeit. v= 225m 70s l 3, 21 ms











