BerechnungBinomialverteilung

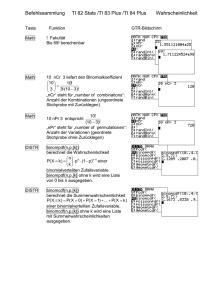
Wahrscheinlichkeitsberechnung Binomialexperimente
Deutung, Umwandlung von Groessenrelationen
Bernoulli-Versuch:
Ein Zufallsexperiment mit nur zwei moeglichen Ausgaengen, wenn nur interessiert, ob ein bestimmtes
Ereignis eingetreten ist, heisst Bernoulli-Versuch.
Bernoulli-Kette:
Ein Zufallsexperiment bei dem ein Bernoulli-Versuch n-mal ausgefuehrt wird heisst Bernoulli-Kette.
Die einzelnen Versuche muessen voneinander unabhaengig sein (Beispiel: Ziehen mit Zuruecklegen),
damit bleibt die Erfolgswahrscheinlichkeit p der einzelnen Versuche immer gleich. Die Laenge der
Kette wird mit der Anzahl der Ausfuehrungen n angegeben.
Zufallsvariable k:
Die Zufallsgroesse k gibt die Anzahl der Erfolge innerhalb einer Bernoulli-Kette an. Die Wertemenge
von k liegt zwischen minimal 0 und maximal n.
k = {0 ... n}
Wahrscheinlichkeit fuer k Erfolge innerhalb einer n langen Bernoulli-Kette:
n

→ binompdf (n; p; k )
P( X = k ) =   * p k * (1 − p ) n−k GTR
k 
binompdf == binomial probabilty density function,
binomisch verteilte Wahrscheinlichkeitsfunktion
Diese Wahrscheinlichkeitsverteilung heisst Binomialverteilung.
Die entsprechende Verteilungsfunktion laesst sich ueber folgende Formel berechnen
k
n
P( X ≤ k ) = ∑   * p k * (1 − p ) n−k GTR

→ binomcdf (n; p; k )
0 k 
binomcdf == binomial cumulativ density function,
binomisch verteilte Wahrscheinlichkeitsverteilungsfunktion
Erwartungswert Binomialverteilung:
E( X ) = n * p
Varianz Binomialverteilung:
V ( X ) = n * p * (1 − p)
Standardabweichung Binomialverteilung:
σ ( x) = V ( X ) = n * p * (1 − p)
Wahrscheinlichkeit 1- σ Umgebung:

→ binomcdf (n; p; µ + σ ) − binomcdf (n; p; µ − σ − 1)
P( µ − σ ≤ X ≤ µ + σ ) = P( X ≤ µ + σ ) − P( X ≤ µ − σ − 1) GTR
Deutung, Umwandlung Groessenrelationen:
Da ueber Grafiktaschenrechner nur die Wahrscheinlichkeiten P ( X = k ) und P ( X ≤ k ) berechnet
werden koennen, ist es fuer die Fragestellung notwendig die Berechnung auf diese beiden
Grundfunktionen zurueckzufuehren. Die Auswahl der entsprechenden Umwandlung erfolgt ueber
Schluesselwoerter in der Aufgabenstellung
Schluesselwort : genau
P( X = k ) = GTR

→ binompdf (n; p; k )
Schluesselwort : hoechstens
P( X ≤ k ) = GTR

→ binomcdf (n; p; k )
Schluesselwort : min destens, wenigstens
P( X ≥ k ) = 1 − P( X ≤ k − 1) GTR

→ 1 − binomcdf (n; p; k − 1)
Schluesselwort : mehr als, groesser
P( X > k ) = 1 − P( X ≤ k ) GTR

→ 1 − binomcdf (n; p; k )
Schluesselwort : geringer als

→ binomcdf (n; p; k − 1)
P( X < k ) = P( X ≤ k − 1) GTR
Schluesselwort : groesser k1 und kleiner k 2
P(k1 < X < k 2 ) = P( X ≤ k 2 − 1) − P( X ≤ k1 ) GTR

→ binomcdf (n; p; k 2 − 1) − binomcdf (n; p; k1 )
Schluesselwort : min destens k1 und hoechstens k 2
P(k1 ≤ X ≤ k 2 ) = P( X ≤ k 2 ) − P( X ≤ k1 − 1) GTR

→ binomcdf (n; p; k 2 ) − binomcdf (n; p; k1 − 1)
Beispiel:
Binomialverteilung mit n = 200; p = 0,24
E ( X ) = n * p = 200 * 0,24 = 48
σ ( x) = V ( X ) = n * p * (1 − p) = 200 * 0,24 * (1 − 0,24) ≈ 6,04
Wahrscheinlichkeitsfunktion
p( X )
X
Verteilungsfunktion