Binomialverteilung mit dem GTR - lehrer.uni

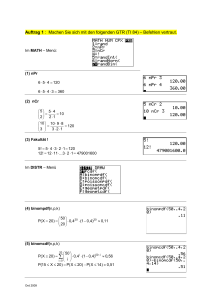
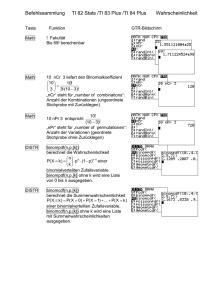
LGÖ Ks
M 12
Schuljahr 2016/2017
Binomialverteilung mit dem GTR
Binomialverteilung P ( X = k ) : Im DISTR-Menü: 0: binompdf ( n, p, k )
Binomiale Summenverteilung P ( X ≤ k ) : Im DISTR-Menü: A: binomcdf ( n, p, k )
Merke: binompdf: probability, also Wahrscheinlichkeitsverteilung P ( X = k )
binomcdf: cumuliert, d. h. addiert, also Summenverteilung P ( X ≤ k )
Achtung: Ist p eine Dezimalzahl, dann muss statt des Kommas (wie üblich) ein Dezimalpunkt
eingegeben werden.
Standardaufgabe: Gegeben ist eine mit den Parametern n und p binomialverteilte Zufallsvariable X.
Die Wahrscheinlichkeit P ( X = k ) bzw. P ( X ≤ k ) soll
a) bei festem n und p für verschiedene Werte von k untersucht werden;
b) bei festem p und k für verschiedene Werte von n untersucht werden;
c) bei festem n und k für alle Werte von p gezeichnet werden.
Lösung:
a) Gib als Funktion Y1 die Wahrscheinlichkeit P ( X = k ) bzw. P ( X ≤ k ) mit der GTRVariablen X anstatt k ein, also
Y1 = binompdf ( n, p, X ) bzw. Y1 = binomcdf ( n, p, X ) ,
und erstelle eine Wertetabelle.
b) Gib als Funktion Y1 die Wahrscheinlichkeit P ( X = k ) bzw. P ( X ≤ k ) mit der GTRVariablen X anstatt n ein, also
Y1 = binompdf ( X, p, k ) bzw. Y1 = binomcdf ( X, p, k ) ,
und erstelle eine Wertetabelle.
c) Gib als Funktion Y1 die Wahrscheinlichkeit P ( X = k ) bzw. P ( X ≤ k ) mit der GTRVariablen X anstatt p ein, also
Y1 = binompdf ( n, X, k ) bzw. Y1 = binomcdf ( n, X, k ) .
Da p nur Werte zwischen 0 und 1 annehmen kann, wählt man Xmin = 0 und Xmax = 1 und
zeichnet das Schaubild mit ZoomFit. (Da die Wahrscheinlichkeiten zwischen 0 und 1
liegen, kann man auch Ymin = 0 und Ymax = 1 nehmen.)
2e_gtr_binomialverteilung