p - warncke

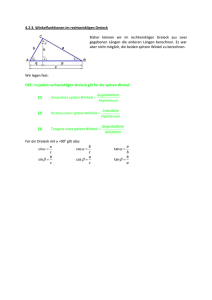
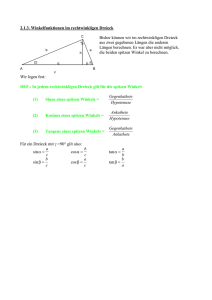
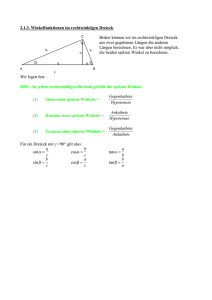
Formelsammlung Abschlussprüfung
BFS Dienstleistung
2014
1/4
Ebene Figuren (A: Flächeninhalt u: Umfang)
Quadrat
Rechteck
a
A=a 2
u=4·a
a
Satz des Pythagoras
Im rechtwinkligen Dreieck gilt: c=√ ( a 2+ b 2)
Dreieck
g⋅h
2
c
B
u=a+b+c
b
h
a 2+ b2=c 2
C
g=a
Parallelogramm
Mit Seiten a ,b , c , d
ac 
⋅h
2
d
D
b
h
a
Kreissektor
b
c
f
b
2
B
e
d
a
⋅r ⋅
A=
°
360

Kreisbogen
b=
A
Kreis
r
⋅r⋅
180°
Kreisring
d =2⋅r
A=⋅r 2 =
c
Kreissektor und Kreisbogen
C
u=abcd
b
u=abcd
Raute
und Diagonalen e , f
e⋅ f
A=
2
a= c 2−b 2 
A=
b
g=a
u=2⋅a2⋅b
c
a
Trapez
h
A= g⋅h
a
u=2·a+2·b
A
A=
b
A=a·b
d
r
⋅d
4
2
u=2⋅⋅r =⋅d
≈3,14
Bestehend aus 2 Kreisen
mit Innenkreisradius r i
und Außenkreisradius r a
ri r
a
A=⋅r 2a −⋅r i2
Maßeinheiten
Länge
1 km = 1000 m
1 m = 10 dm = 100 cm = 1000 mm
1 dm = 10 cm = 100 mm
1 cm = 10 mm
Fläche
1 m² = 100 dm² = 10000 cm²
1 dm² = 100 cm²
1 cm² = 100 mm²
1 km² = 100 ha ; 1 ha = 100 a = 10000 m²
Volumen
1 ml = 1 cm³
1 m³ = 1000 dm³ = 1000 l = 1000 000 ml
Masse
1 t = 1000 kg = 1000 000 g ; 1 g = 1000 mg
Formelsammlung Abschlussprüfung
BFS Dienstleistung
2014
2/4
Körper (V : Volumen O : Oberfläche G: Grundfläche M: Mantelfläche)
Würfel
Quader
c
V =a
3
V=a·b·c
a
O=6⋅a 2
a
a
O=2 ab2 ac2 bc
Prisma
Zylinder
V =G⋅h
h
V =⋅r 2⋅h
M
M =u⋅h
O=2⋅GM
b
a
G
h
M =2⋅⋅r⋅h
2
O=2⋅⋅r 2⋅⋅r⋅h
G
r
Spitze Körper
Quadratische Pyramide
1
V = ⋅G⋅h
3
V=
2
O=GM
a ⋅h
3
hs
h
M =2⋅a⋅hs
a
O=a 2+ 2⋅a⋅hs
a
Kegel
V=
⋅r 2⋅h
3
M =⋅r⋅s
O=⋅r 2⋅r⋅s
Kugel
s
h
4
V = ⋅⋅r 3
3
r
O=4⋅⋅r 2
r
Prozentrechnung
G: Grundwert
W: Prozentwert
p : Prozentsatz (in Prozent)
W=
Zinseszinsen (exponentielles Wachstum)
K 0 : Kapital am Anfang
Zinsfaktor
K n : Kapital nach n Jahren
n : Zeit in Jahren
p : Prozentsatz (in Prozent)
G⋅p
100
p=
q=
W
⋅100
G
p
100+ p
=(1+
)
100
100
K n =K 0⋅q
n
G=
W
⋅100
p
Formelsammlung Abschlussprüfung
Binomische Formeln
ab2=a 22· a ·bb 2
BFS Dienstleistung
a – b2=a 2 – 2 · a · bb2
2014
3/4
2
2
ab ·a – b=a – b
Potenzgesetze
a m · a n=a m+ n
a · b =(a · b)
a m : a n =a m− n
a n : b n =(a :b)n
n
n
n
m n
(a ) =a
a 0=1
m ·n
a−n=
Wurzelgesetze
√n a⋅b=√n a⋅√n b
√ √ a= √ √ a= √ a
√n a : √n b=√n a :b
n m
m n
m⋅n
( √ a) =√ a m
m
n
n
Quadratische Gleichungen
p=
Allgemeine Form ax 2 + bx+ c=0 ∣: a
2
x  pxq=0
Die Normalform
wenn
( ) −q ≥ 0
p
2
b
c
, q=
a
a
hat die Lösung
p
x1,2 =− ±
2
2
, sonst keine Lösung.
 
2
p
−q
2
Lineare Funktionen: y = m · x + b
Quadratische Funktionen:
m: Steigung der Geraden g durch die
Punkte P 1 (x 1∣y 1 ) und P 2 (x 2∣y 2 )
y −y
m= 2 1
x 2− x 1
b: Schnittpunkt mit der y-Achse
Allgemeine Form: y=a⋅x 2b⋅xc
y
Scheitelpunktform y=a⋅ x− x s 2 y s
Scheitelpunkt bei S ( x s∣y s)
y
P2
y 2− y 1
P1
xs
b
ys
x 2− x 1
x
x s=−
p
2
S ( x s∣y s)
x
1
an
Formelsammlung Abschlussprüfung
BFS Dienstleistung
Trigonometrie (im rechtwinkligen Dreieck)
Im rechtwinkligen Dreieck gilt:
c

a
b
2014
4/4
a
c
Gegenkathete durch Hypotenuse
cos =
b
c
Ankathete durch Hypotenuse
tan =
a
b
Gegenkathete durch Ankathete
sin =
Beschreibende Statistik / Stochastik
Arithmetisches Mittel (Mittelwert x )
x=
x1 + x 2+ x3 + ...+ x n
n
Spannweite
„Summe durch Anzahl“
Spannweite = Max - Min
„Größter Wert minus kleinster
Wert“
Median (Zentralwert)
In einer Stichprobe, deren Werte nach der Größe geordnet sind, stehen links und rechts vom
Median gleich viele Werte. Der Median ist also die Mitte der Liste. Bei einer geraden Anzahl
von Werten ist der Median deswegen nicht eindeutig bestimmt (man nimmt dann z.B. das
arithmetische Mittel der in der Mitte stehenden Werte).
Diagramme
Säulendiagramm prozentual (Wert → Höhe)
Kreisdiagramm (Wert → Winkel)
Summe aller prozentualen Werte ist rd. 100%.
Summe aller Winkel ist rd. 360° ; 1 % ≙ 3,6°.
Wahrscheinlichkeitsrechnung
Ergebnisraum („alle Ergebnisse“)
Ereignismenge E („gewünschte Ergebnisse“)
Wahrscheinlichkeit für das Ereignis E
P (E)=
Gegenwahrscheinlichkeit
∣E∣
Anzahl der gewünschten Ergebnisse
=
Anzahl aller möglichen Ergebnisse ∣Ω∣
P (E )=1− P (E)
Pfadregeln
Für mehrstufige Zufallsexperimente gilt für die
Wahrscheinlichkeit eines Pfades:
P ( Aund B)=P ( A)⋅P (B)
P ( Aoder B)=P ( A)+ P (B)
sofern A und B voneinander unabhängig sind.
Bezogen auf das Baumdiagramm rechts
P (E)=P (E 1)+ P (E 2 )= p1⋅p2 +q1⋅q 2
Dargestellt in einem Baumdiagramm gehören
zum Ereignis E die Einzelereignisse E 1 und
E2 .