1 2 3 N - Antriebstechnik.fh

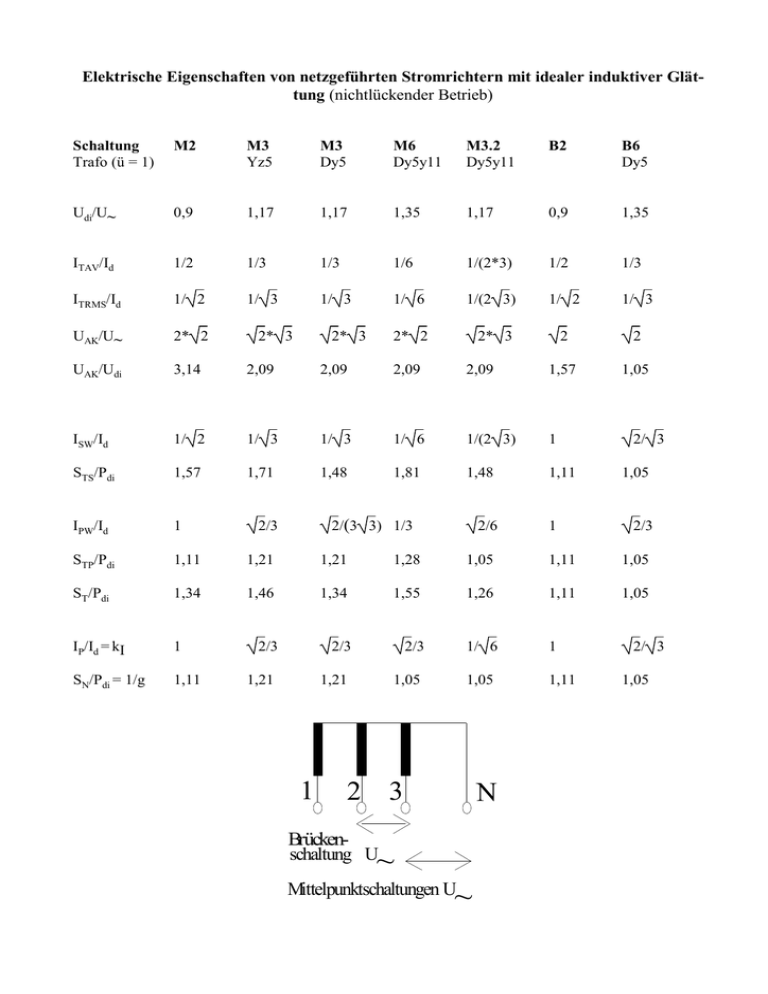
Elektrische Eigenschaften von netzgeführten Stromrichtern mit idealer induktiver Glättung (nichtlückender Betrieb)
Schaltung
Trafo (ü = 1)
M2
M3
Yz5
M3
Dy5
M6
Dy5y11
M3.2
Dy5y11
B2
B6
Dy5
Udi/U~
0,9
1,17
1,17
1,35
1,17
0,9
1,35
ITAV/Id
1/2
1/3
1/3
1/6
1/(2*3)
1/2
1/3
ITRMS/Id
1/ 2
1/ 3
1/ 3
1/ 6
1/(2 3)
1/ 2
1/ 3
UAK/U~
2* 2
2* 2
2* 3
2
2
UAK/Udi
3,14
2,09
2,09
2,09
2,09
1,57
1,05
ISW/Id
1/ 2
1/ 3
1/ 3
1/ 6
1/(2 3)
1
STS/Pdi
1,57
1,71
1,48
1,81
1,48
1,11
IPW/Id
1
STP/Pdi
1,11
1,21
1,21
1,28
1,05
1,11
1,05
ST/Pdi
1,34
1,46
1,34
1,55
1,26
1,11
1,05
IP/Id = kI
1
2/3
2/3
2/3
1/ 6
1
SN/Pdi = 1/g
1,11
1,21
1,21
1,05
1,05
1,11
2* 3
2* 3
2/(3 3) 1/3
2/3
1
2/6
2 3
N
Brückenschaltung U
~
Mittelpunktschaltungen U
~
1
2/ 3
1,05
2/3
2/ 3
1,05
Elektrische Berechnung der idealen, netzgeführten Stromrichter
Mittelwerte kennzeichnen eine mittlere Wirkung, wenn Ursache und Wirkung linear zusammenhängen, z. B. Motordrehzahl n = k U. Wenn die Wirkung der Ursache mit Verzögerung folgt, führt das bei genügend hoher Frequenz der
Anregung dazu, daß die Wirkung nur dem Mittelwert der Anregung folgt. Gemessen werden Mittelwerte mit Drehspulinstrumenten oder Digitalinstrumenten im DC-Bereich. Mittelwerte werden vorzeichenrichtig addiert.
T
Definition:
2π /p
T
1
u = ∫u(t ) * dt
T0
1
i = ∫i (t ) * dt
T0
u
Ungesteuerte Schaltungen:
Bei ungesteuerten SR-Schaltungen führt jeweils das Ventil
(Diode) mit der positivsten Anodenspannung den Strom; am
Schnittpunkt der Spannungspulse erfolgt die natürliche Kommutierung zum nächsten Ventil. Unter Vernachlässigung der
0
− π /p
π/p
Spannungsabfälle (werden später berücksichtigt) erhält man die
maximale Ausgangsgleichspannung durch Integration und Mittelung über einen Spannungspuls:
π/ p
U di =
1
2U ~ cos ω t * dω t
2π / p − π∫/ p
p
U di = 2U ~
sin π / p
für
π/p
p≥2
U di = 2U ~
ωt
1
für
π
p=1
∞
1
2
3
6
12
U di / U ~
2
π
2 2
π
3 6
2π
3 2
π
6( 3 − 1)
π
2
U di / U ~
0,45
0,9
1,17
1,35
1,4
1,41
Für die Gleichrichtung maßgebliche Spannung U~ : M-Schaltungen = USM (Sternspannung)
B-Schaltungen = US (verkettete Spannung)
Gesteuerte Schaltungen:
Die Stromübergabe der steuerbaren Ventile (Thyristoren) wird um den Steuerwinkel α verzögert. Bei der Berechnung
wird das Integrationsintervall ebenfall um α verschoben. Der Steuerwinkel α kann maximal zwischen 0 und 180o verändert werden.
Bei nichtlückendem Betrieb (Ld=∞ ) schließen die
Ausgangsspannungspulse nahtlos aneinander an und
es gilt:
Bei Lückbetrieb (ohm'sche Last) endet der Stromfluß bei π/2 bevor das nächste Ventil eingeschaltet
hat:
α + π/ p
U di α
1
2U ~ cosω t * dω t
=
2π / p α − ∫
π/ p
U diα = 2U ~
sin(π / p)
cosα
π/p
U diα = U di cosα
I TAV =
1
Id
z *q
π /2
U di α
1
2U ~ cosω t * dω t
=
2π / p α − ∫
π/ p
U diα = U di
1 − sin(α − π / p)
2 sin(π / p)
U diα = 0
für α ≥
I TAV =
π π
+
2 p
U diα
2U ~ p 
π 
=
1 − sin(α − )
z *q * R
z * R 2πq 
p 
q = Zahl der miteinander kommutierenden Ventile
z = Zahl der Parallelschaltungen oder -ventile
Gleichspannung gesteuerter Stromrichter
1,25
Pulszahl
Udia/Udi
1
Lückbetrieb
0,75
2
0,5
3
6
0,25
0
12
-0,25
-0,5
nichtlückend
-0,75
-1
-1,25
0
30
60
90
120
150
180
Steuerwinkel
Effektivwerte kennzeichnen eine Wirkung, die unabhängig von der Richtung der Ursache ist, bzw. dem Produkt zweier abhängiger Größen entspricht (quadratischer Zusammenhang), z. B. P = U*I = U2/R=I2*R
(positive Wirkleistung entsteht durch positive oder negative Strom- bzw. Spannungswerte.) Effektivwerte sind wichtig bei
der Berechnung der thermischen Belastung von Netzen, Trafos und Bauelementen. Meßbar sind sie durch Instrumente
mit quadratischem Zusammenhang von Wirkung (Drehwinkel des Zeigers) und Ursache (Strom), wie Dreheisen- und
Hitzdrahtinstrumente. Bei digitalen Instrumenten muß darauf geachtet werden, ob sie echte Effektivwerte anzeigen
(TRUE RMS). Effektivwerte werden quadratisch addiert!
T
Definition:
U RMS =
1 2
u (t )dt
T∫
0
Nichtlückender Betrieb:
α+ π/ p
U diα RMS
p
=
2π α − ∫
π/ p
(
Lückbetrieb: Die Stromblöcke und damit die Integrationsgrenzen enden wieder bei π/2:
)
2
2U ~ cosω t dω t
2π
p
cos 2α
2π
p
π /2
U diα RMS
sin
U diα RMS = U ~ 1 +
I TRMS =
1
Id
z q
U diα RMS = U ~
I TRMS =
(
)
2
p
=
2
U
cos
ω
t
dω t
~
2π α − ∫
π/ p
p
2π
π π

π 
1
− α − sin 2α − 
 +
2

p 
2 p
U diα RMS
z q *R
Die Ausgangsspannung eines SR setzt sich aus einem Gleichanteil und einem
Wechselanteil zusammen:
2
U diα RMS = U di2 α + U wi
α
Uw
α
U di
U diα RMS
α
Leistungen
Ziel der Leistungselektronik ist das möglichst verlustfreie Anpassen elektrischer Wirkleistung (geeigneter Strom- und
Spannungsverlauf) an den Verbraucher. Leistung, die zwischen Verbraucher und Quelle hin- und herpendelt (Blindleistung) ist unerwünscht, da sie von der Quelle bereitgestellt werden muß und auch Leitungsverluste erzeugt. Nachfolgend
sind nach einigen Leistungsdefinitionen die Verhältnisse in netzgeführten Stromrichtern gezeigt.
Wirkleistung: P = p( t ) = u( t ) * i ( t )
Momentanleistung: p(t) = u(t)*i(t)
Die Wirkleistung stellt die über einen Betrachtungszeitraum T gemittelte Momentanleistung dar.
Leistungsberechnung für beliebige Kurvenformen durch komplexe Größen:
Strom und Spannung können in einzelne Schwingungen zerlegt werden:
Untersucht werden soll das Produkt der Spannung mit der Frequenz mω mit dem Strom der Frequenz nω
I = i$n exp j (nω t + ψ n )
U = u$m exp j (mω t + ϕ m )
komplexe Leistung: Pm,n =
1
1
U I * = u$m i$n e j ( m− n) ω t e j ( ϕ m − ψ n )
2
2
u$m i$n
= U RMS I RMS
2 2
Scheinleistung:
Sm,n = Pm,n =
Wirkleistung:
Pm,n = ℜ Pm,n =
( )
1 $
u$min cos(m − n)ω t * cos(ϕ m − ψ n )
2
Pm,n = S m,n cos(ϕ m − ψ
Blindleistung:
Qm,n =
2
n)
( )
Pm,n − ℜ Pm,n
2
für
für
Pm,n = 0 für
m≠ n
= Sm2 ,n − Pm2,n
Qm,n = S m,n 1 − cos 2 (ϕ m − ψ n )
Qm,n = S m,n = D
m=n
m≠ n
für m = n
(Verschiebungsblindleistung)
(Verzerrungsblindleistung)
Zusammenfassung:
Wirkleistung wird nur dann transportiert, wenn Strom und Spannung gleiche Frequenz haben und nicht 90o phasenverschoben sind.
Oberschwingungen von Strom und Spannung tragen nur zur Wirkleistung bei, wenn sie gleiche Frequenz und Phase
haben.
Blindleistung entsteht bei ungleicher Frequenz von Strom und Spannung (Verzerrungsblindleistung) oder wenn Strom
und Spannung gleichfrequent und phasenverschoben sind (Verschiebungsblindleistung).
Leistungsdiagramm mit idealer Glättungsdrossel:
Im Leistungsdiagramm werden die Wirkleistung in x-Richtung, die Grundschwingungsblindleistung in y-Richtung aufgetragen.
a) Sinusförmige Anteile von Strom und Spannung auf der Wechselstromseite
1
u$ * i$ = U 1 * I1
2
S1 = U di I d = Pdi
S1 =
P = S1 cosϕ
z.B. Drehstromnetz:
S1 = 3U PM I P = 3U P I P
ϕ = Verschiebung zw. Spannungs- und Stromgrundschwingung = Steuerwinkel α
P = U di I d cosα
Q1 = U di I d sin α = S12 − P 2 = S1 1 − cos 2 α
Bei vollgesteuerten SR-Schaltungen mit aktiver Last und idealer
Glättung beschreibt der Zeiger S1 mit steigendem α einen Halbkreis.
Bei α = 0o ist die Wirkleistung P = Pdi gleich der Grundschwingungsscheinleistung S1. Bei α = 90o wird (bei konstantem Strom)
die abgegebene Spannung und damit die Wirkleistung = 0 und die
Scheinleistung besteht aus Blindleistung. Für α > 90o wird die
Wirkleistung negativ (die Last speist Leistung an den SR zurück).
S1
Q
1
α
P
b) Nichtsinusförmige Ströme, sinusförmige Netzspannung
S = U RMS I RMS = U 12 I12 + U 12 ∑ Iν2 = S12 + D 2 =
gesamte Scheinleistung
P 2 + Q12 + D 2
ν> 1
Q = Q12 + D 2
gesamte Blindleistung
Grundschwingungsfaktor g =
Verzerr.blindleistung D =
S1 Pdi
=
S
S
cos ϕ = cos α =
Verschiebungsfaktor
P
S1
S 2 − S12 = k * S
Klirrfaktor
k = 1−
Leistungsfaktor
λ=
S12
= 1 − g2
2
S
P
= g * cos α
S
Der Leistungsfaktor beschreibt die Minderausnutzung der elektr. Einrichtungen gegenüber der größtmöglichen Leistungsübertragung bei gleichphasigem,sinusförmigen Strom.
Vollständiges Leistungsdiagramm:
Q1
D
D
S1=const
D
S
D
S
S1
Q
S1
Q1
1
α
Pd
dreidimensionale Darstellung
P
Q
α
P
zweidimensionale Darstellung
Der Wirkungsgrad ist das Verhältnis abgegebene Wirkleistung/aufgenommene Wirkleistung: η =
Pab
Pauf
Bisher wurden in den Schaltungen keine Verluste berücksichtigt, d. h. Pab = Pauf = Pd = Udiα*Id ; der
Wirkungsgrad η nach den o.g. Formeln = 1.