1. Sem - RFH
Werbung

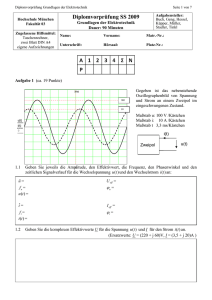
Rheinische Fachhochschule Köln Matrikel-Nr. Nachname Dozent Ianniello Semester Klausur BP K9 Datum März 2013 Fach Grundlagen der Elektrotechnik Urteil Ergebnis: _____ Punkte Genehmigte Hilfsmittel: Formelsammlung (Kuchling), keine losen Blätter Taschenrechner, kein Handy Papier, Lineale, Stifte Zeit: 120 Minuten Anmerkungen Tragen Sie den/die Lösungs-Buchstaben bzw. das Ergebnis in das freie Feld rechts neben der Frage ein. Keine, eine aber auch mehrere Antworten sind möglich Teilpunkte gibt es nur für eine lesbare und strukturierte Berechnung (allg. Formel als Ansatz, sofort nachvollziehbare Berechnung aus zusammenhängenden Gleichungen) Tragen Sie das Ergebnis in das freie Feld rechts neben der Frage ein. Ein leeres Feld wird als Unsicherheit angesehen, daher nicht mit der vollen Punktzahl bewertet, auch wenn die Berechnung vorliegt. Als Ergebnis zählen keine Brüche oder Formeln, nur die erfragte Größe. Richtige Ergebnisse ohne Einheit erhalten nur 50% der vollen Punktzahl. Zahlenschlangen (1234) ohne Tausenderpunkt oder „0,0...“-Zahlen (z.B. 0,02 A statt 20 mA oder 2·10-2A) vermindern die Punktzahl. Die Präsenz eines Handys wird mit einem Täuschungsversuch gleichgesetzt. Die Klausur wird dann sofort eingezogen. Viel Erfolg ! K9_13-03_L.odt Seite 1 von 15 Prof. Dr. R. Ianniello K9 Grundlagen der Elektrotechnik 1. Elektrostatik 1 Ein Elektroskop ist positiv geladen, am Zeiger ist ein Ausschlag zu erkennen. Jetzt führt man an das Elektroskop einen negativ geladen Stab heran, ohne das es zu einer direkten Berührung kommt. Wie ändert sich der Ausschlag des Zeigers? Er A) wird kleiner, B) ändert sich gar nicht, C) wird größer. 2 Ein geladenes Staubteilchen mit einer Masse von 15 ng schwebt im Feld eines horizontalen Plattenkondensators, an dem eine Spannung von 500 V angelegt wird. Die Platten sind horizontal in einem Abstand von 5,0 mm angeordnet. Berechnen Sie die Ladung des Staubteilchens. 3 A 2 1,47 fC 6 Am Punkt A befinde sich eine Ladung q = 3,5 mC. Wie groß ist die abstoßende Kraft auf diese Ladung, die sich in der Nähe von q1 und q2 befindet? a = 23 cm, α = 30°, β = 60°. a Wie groß sind die beiden Teilkräfte, die q abstoßen? F1= 231 kN F2 = 260 kN 6 b Wie groß ist die Gesamtkraft, und die Richtung, in die q abgedrängt wird? F = 348 kN φ = 108° 6 Summe 20 Lösung zu Aufgabe 1.1 Durch Influenz werden die negative Ladungsträger aus dem Anschluss des Elektrometers ins Innere gedrängt. Dort kompensieren sie die positiven Ladungen (Elektronenmangel) und die abstoßenden Kräfte werden kleiner. K9_13-03_L.odt Seite 2 von 15 Prof. Dr. R. Ianniello K9 Grundlagen der Elektrotechnik Lösung zur Aufgabe 1.2 Lösung zur Aufgabe 1.3 K9_13-03_L.odt Seite 3 von 15 Prof. Dr. R. Ianniello 2. Gleichstrom # K9 Grundlagen der Elektrotechnik Frage Antw. P. 1 In der Schaltung sind drei Akkus mit je einer Nennspannung UN = 1,25 V in Reihe geschaltet. Mit dem Schalter kann der Stromkreis umgeschaltet werden. a In der Schalterstellung „Aus“ zeigt das Amperemeter Null Ampere an. Wie groß ist der Widerstand am Schalter in dieser Stellung? →∞ 2 b Wie groß ist die Stromstärke in dem Leitungsabschnitt C-D bei Schalterstellung 2, wenn der Verbraucher einen Widerstand von R = 250 Ω hat? 10 mA 2 2 Wie groß ist der Ersatzwiderstand zwischen den Klemmen 1-2, wenn die Strecke 3-4 kurzgeschlossen ist? 14 kΩ 3 3 a Die Schaltung ist symmetrisch, was im Hinblick auf die Potenziale zu Besonderheiten führt. Finden Sie eine berechenbare Ersatzschaltung und skizzieren Sie sie. b Wie groß ist der Ersatzwiderstand der Schaltung? 7 3,357 kΩ 6 4 Es liegt eine Reihenschaltung aus zwei unterschiedlichen ohmschen Widerständen vor. A) Der Strom hat überall in der Schaltung denselben Wert, B) Die Spannung an den Widerständen ist gleich groß, C) Die Art der Spannung hat keinen Einfluss auf den Strom, D) Der Strom erhöht sich, wenn man einen Kondensator sehr großer Kapazität zuschaltet. A 2 5 Was geschieht, wenn man in einer Parallelschaltung einen zusätzlichen Widerstand einbaut? A) Der Strom wird kleiner, B) der Gesamtwiderstand wird kleiner, C) Die Spannung wird größer, D) Die Spannung wird kleiner B 2 Summe 20 K9_13-03_L.odt Seite 4 von 15 Prof. Dr. R. Ianniello K9 Grundlagen der Elektrotechnik Lösung zur Aufgabe 2.1 b) Lösung zur Aufgabe 2.2 Lösung zu Aufgabe 2.3 K9_13-03_L.odt Seite 5 von 15 Prof. Dr. R. Ianniello K9 Grundlagen der Elektrotechnik 3. Sensoren/Halbleiter/Transistor # Frage 1 Antw. P. In einer Transistorschaltung sind die Potenziale φB, φC und φE durch Messung bekannt. IC = 4 mA 3 IV = 251,5 µA 3 Wie groß sind die Ströme IC, IV und Iq in den Widerständen RC, RV und Rq ? Iq = 207,3 µA 3 50 mA 6 2 Wie groß wäre in Aufgabe 3.1 der Basisstrom, wenn IV = 200 mA und Iq = 150 mA 3 Ein Kupferdraht der Länge 170 m habe eine Querschnittsfläche von 0,5 mm². Die spezifische Leitfähigkeit des Kupfers sei 56 m/(Ωmm²) , der Temperaturkoeffizient 3,93·10-3 1/K. a Wie groß ist der Drahtwiderstand bei 20°C ? 6Ω 3 b Wie groß ist der Drahtwiderstand bei 62,5°C ? 7Ω 3 4 Ein LDR verringert seinen Widerstandswert wenn es A) wärmer, B) kälter, C) heller, D) dunkler wird, oder wenn E) die Spannung steigt, F) die Spannung sinkt, oder G) ein LDR ist kein Widerstand, daher trifft keine der Aussagen zu. C 2 5 Wofür steht beim Transistor das Kurzzeichen C ? Für die A) Kapazität, B) Ladung, C) für den „Collector“, D) für den „Connector“, E) für das Durchschalten des Transistors C 2 Summe 25 K9_13-03_L.odt Seite 6 von 15 Prof. Dr. R. Ianniello K9 Grundlagen der Elektrotechnik Lösung zur Aufgabe 3.1 Lösung zur Aufgabe 3.2 Lösung zur Aufgabe 3.3 K9_13-03_L.odt Seite 7 von 15 Prof. Dr. R. Ianniello 4. Elektrochemie # K9 Grundlagen der Elektrotechnik Frage Antw. P. 1 Welche Ladungsmenge in Coulomb hat ein 9V-Block gespeichert, der voll aufgeladen ist? („Kapazität“ 1 Ah, Nennspannung UN = 8,4 V, Ladestrom 11 mA) 3,6 kC = 3.600 C 2 2 Wie groß ist die Aufladezeit für den Akku, Bauart 9V-Block, wenn seine „Kapazität“ 0,11 Ah, seine Nennspannung 8,4 V und der Ladestrom 11 mA beträgt? 14 h (real) 6 3 Ein Akku habe eine „Kapazität“ von 4 Ah und eine Nennspannung von 1,25 V. Er ist bei einem Ladestrom von 400 mA geladen worden. Wie lange könnte er einen Entladestrom von 0,1 A liefern, wenn seine „Kapazität“ dabei von 100% auf 90% sinkt? Verluste seien vernachlassigbar. 4h 3 4 Wie viel elektrische Arbeit in Wattsekunden könnte eine voll aufgeladene Mignonzelle („Kapazität“ = 0,5 Ah, UN = 1,25 V), wenn sie ihre gesame gespeicherte Energie abgäbe? 2.250 Ws 3 Anode 1 5 Aus welchen drei wesentlichen Bauteilen ist ein galvanisches Element aufgebaut? Elektrolyt 1 Katode 1 6 Wovon hängt das Potenzial eines Redoxpaares ab? Von A) der Molmasse, B) der Oxidationsstufe der Partner, C) dem Atomgewicht, D) dem metallischen Charakter B 2 7 Auf welches Redoxpaar bezieht sich das Standardpotenzial der elektrochemischen Spannungsreihe? H2 + H2O / H3O+ (Wasserstoff) 3 8 Wie nennt man die Kombination aus einem Atom und dem Ion desselben Elements? Redoxpaar 3 Summe 25 K9_13-03_L.odt Seite 8 von 15 Prof. Dr. R. Ianniello K9 Grundlagen der Elektrotechnik Lösung zur Aufgabe 4.1 Lösung zur Aufgabe 4.2 Lösung zur Aufgabe 4.3 Lösung zur Aufgabe 4.4 K9_13-03_L.odt Seite 9 von 15 Prof. Dr. R. Ianniello K9 Grundlagen der Elektrotechnik 5. Magnetismus / Induktion # Frage Antw. P. 1 Beschreiben Sie drei Unterschiede zwischen den magnetischen und elektrischen Größen: Ladung, Feldlinien und Polen. (Vergleiche, keine Einzelbeschreibungen) a Es gibt eine elektrische, aber keine magnetische Ladung 2 b Die elektrischen Feldlinien sind offen, die magnetischen geschlossen 2 c Elektrische Pole: Plus und Minus, magnetischen Pole: Nord und Süd 2 2 Eine Spule mit der Induktivität L = 100 µH wird an eine vorgegebene Spannung u(t) angeschlossen. Zeichnen Sie den zugehörigen Stromverlauf i(t), wenn i(t=0s) = 0 A im rechten Diagramm. 9 3 Bei einem Induktionsherd wird die Speise erhitzt, weil A) ein starkes elektrisches Feld Ströme im Topfboden induziert, B) ein wechselndes Magnetfeld die Weißschen Beirke im Topfboden ständig umpolt, C) die Wassermoleküle in der Speise durch ein hochfrequentes Wechselfeld zum Schwingen gebracht werden und damit die Speise erhitzt wird, D) die magnetische Wärmestrahlung den magnetischen Topfboden und darüber die Speise erwärmt. B 2 4 Spannung lässt sich in einen Draht induzieren, wenn man A) einen starken Strom durch den Draht schickt, und den Draht dabei erwärmt, B) den Draht so in ein Magnetfeld hält, dass die magnetischen Feldlinien die gleiche Richtung haben wie der Draht C) den Draht elektrisch auflädt und erhitzt, C) den Draht in einem Magnetfeld senkrecht zu den magnetischen Feldlinien hin und her bewegt, D) einen Magneten an einem Draht vorbei bewegt. C, D 4 5 Wie funktioniert die Wirbelstrombremse z.B. an einem ICE der Deutsche Bahn AG? Filtern Sie die richtigen Aussagen heraus und sortierten Sie sie in der richtigen Reihenfolge: A) Das Magnetfeld des Bremsmagneten induziert eine Wirbelspannung in der Schiene, B) Der Bremsmagnet erzeugt eine Hallspannung, C) Die Wirbelspannung erzeugt einen Wirbelstrom, D) der Bremsmagnet wird eingeschaltet, E) Die Hallspannung induziert einen Wirbelstrom, F) Die Wirbelspannung induziert eine bremsende Lorentzkraft, G) die Hallspannung erzeugt nach der Lenzschen Regel ein Gegenmagnetfeld, H) Der Wirbelstrom erzeugt ein bremsendes Gegenmagnetfeld. D, A, 6 C, H Summe K9_13-03_L.odt 27 Seite 10 von 15 Prof. Dr. R. Ianniello K9 Grundlagen der Elektrotechnik Lösung zur Aufgabe 5.2 K9_13-03_L.odt Seite 11 von 15 Prof. Dr. R. Ianniello 6. Wechselstrom # K9 Grundlagen der Elektrotechnik Frage Antw. P. 1 In einem Wechselstromkreis wurden gemessen: U = 169,7 V und I = 400 mA. Die Fasenverschiebung betrage 30°, wobei der Strom der Spannung bei einer Frequenz von 50 Hz vorausläuft. Beschreiben Sie die Gleichungen für u(t) und i(t). a u(t) = 169,7V·√2 ∙sin(2π50Hz·t·(180°/π)) 3 b i(t) = 400mA·√2 ∙sin((2π50Hz·t·(180°/π) +30°) 3 f = 50 Hz 2 a Wie groß ist der Widerstand der Parallelschaltung in Exponentialform? 7,07 Ω·e-j45° 6 b Wie groß ist der Scheinwiderstand der Schaltung in Exponentialform? 11,18 Ω·e-j26,6° 2 c Wie groß ist die Spannung am Parallelwiderstand in Exponentialform bei t = 8ms, wenn u(t) = Umax sin(ωt) mit Umax = 5 V? 1,859 V·e-j18,4° 6 I : Effektivwert U 2 II: Scheitelwert Umax 2 3 Sie sehen das Bild einer sinusförmigen Wechselspannung. Ordnen Sie den römischen Zahlen die richtige Bezeichnung und das entsprechende Formelzeichen zu! III: Spitze-SpitzeSpannung USS 2 IV: Periodendauer T 2 Summe K9_13-03_L.odt 28 Seite 12 von 15 Prof. Dr. R. Ianniello K9 Grundlagen der Elektrotechnik Lösung zur Aufgabe 6.2 K9_13-03_L.odt Seite 13 von 15 Prof. Dr. R. Ianniello K9 Grundlagen der Elektrotechnik Anhang K9_13-03_L.odt Seite 14 von 15 Prof. Dr. R. Ianniello K9_13-03_L.odt K9 Grundlagen der Elektrotechnik Seite 15 von 15