AAAC_NF Kapitel 5

ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
Kapitel 5 Die Halogene (7. Hauptgruppe; 17.
Gruppe)
5.1 Allgemeines
F
Fluor (fluor lat. fließend; aus Flussspat (Fluorit = CaF2)
elementares Fluor = F2
farbloses, sehr reaktives Gas, giftig, ätzt Glas!
Cl
Chlor (chloros griech. gelb-grün)
elementares Chlor = Cl2
gelb-grünes, sehr reaktives Gas, giftig
Br
Brom (bromos griech. stinkend)
elementares Brom = Br2
rotbraune Flüssigkeit, Dämpfe giftig
I
Iod (englisch: iodine; iodos griech. violett)
elementares Iod = I2 violett-schwarzer Feststoff; Halbmetall; lässt sich sublimieren:
Sub lim ation
fest   → gasförmig
At
Astat (astatos griech. instabil) radioaktives Element
langlebigstes Isotop 210At; t1/2 (Halbwertszeit) = 8,3 h; Astat ist ein Metall
Einige Eigenschaften:
F
Cl
Br
I
2
5
2
5
2
10
5a
Valenzelektronen
2s 2p
3s 3p
4s (3d )4p
5s2(4d10)5p5
IE (eV)
17,42
13,01
11,84
10,45
b
EA (eV)
3,35
3,61
3,36
3,06
158,8
242,6
192,8
151,1
∆HDiss (X–X) (kJ/mol)
–
Ionenradius (X ) (pm)
133
184
196
230
Siedepunkte (°C)
–188,1
–34
59,5
185,2
Schmelzpunkte (°C)
–218,6
–101
–7,25
113,6
a
Die d-Elektronen zählen in Wahrheit nicht zu den Valenzelektronen, sie stehen nämlich nicht für
„Chemie“ zur Verfügung. b die Aufnahme eines Elektrons ist exotherm für die Halogenatome,
dennoch erscheint der Energiebetrag mit einem positiven Vorzeichen; EA(Cl) = IE(Cl–) (siehe
Edelgase)
In der Natur kommen die Halogene (X2) wegen ihrer hohen Reaktivität nicht elementar vor,
sondern stets als Verbindung.
Elektronenkonfiguration: es fehlt ein e– zur Edelgaskonfiguration →die Bildung von Anionen X– ist
sicher eine wichtige Reaktion.
Dissoziationsenergie der X2:
X2
2 X·
F << Cl > Br > I > At
Abstand dX–X (pm) = 143 (F2) < 199 (Cl2) < 228 (Br2) < 266 (I2) (für die Gasmoleküle)
Eigentlich müsste die Dissoziationsenergie stetig innerhalb der Gruppe bis zum Fluor steigen. Bei
Fluor liegt also eine Labilisierung der F–F-Bindung vor. Erklärt werden kann diese (u.a) Anhand
des Modells der Valenzstrichformel:
33
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
********************************************************************************
<EXKURS: VALENZSTRICHFORMEL – LEWIS-FORMEL - DAS VSEPR-MODELL>
A) Die Elektronentheorie der Valenz – Valenzstrichformel (1)
Prinzip: Die Valenzelektronen eines Atoms werden entweder als · oder als ↑ dargestellt.
Elektronenpaare werden als — (Bindungen) oder  (freie Elektronenpaare) dargestellt.
Beispiele für Lewis-Formeln:
Atome:
1. Periode
H
2. Periode
Be
Li
He oder He
B
C
N
O
F oder F
Ne
Moleküle (Bildung von; siehe Kapitel 4)
H
H + H
H
oder
oder H H
H
+
H
H
H
Achtung, diese Ausdrücke
sind nicht nur antiquiert
sondern auch irreführend
Moleküle (Strukturen)
H
H
O
H
H
Bindungselektronenpaare
freie Elektronenpaare Molekül - Name - Anzahl der Valenzelektronen
H2 - Diwasserstoff - VE = 2
H2O - Wasser - VE = 2 × 1 + 1 × 6 = 8
Cl Cl
Cl2 - Dichlor - VE = 2 × 7 = 14
B) Die Elektronentheorie der Valenz – Erstellen von Valenzstrichformeln (2)
Regeln:
1) Ermitteln der Gesamt-Valenzelektronenzahl
2) Verteilen der Valenzelektronen paarweise auf Bindungen (bindende Elektronenpaare) und
freie Elektronenpaare auf möglichst symmetrische Art und Weise
3) Bei Molekülen aus mehreren verschiedenen Atomen wird immer die symmetrischere
Variante bevorzugt. Zwischen den Atome gibt es mindestens ein bindendes Elektronenpaar
4) Die Valenzelektronen werden so verteilt, dass Bindungen zwischen den Atomen eine
Bindungsordnung von 1, 2 (Doppelbindung) oder 3 (Dreifachbindung) haben
5) Die Gesamtzahl der Velenzelektronen um ein Atom darf im Fall von Elementen der
Perioden 1 und 2 die Zahl 8 nicht übersteigen (Oktettregel)
6) Für die elemente der 3. und weiteren Perioden kann von der Oktettregel abgewichen
werden.
7) Restliche ungepaarte Elektronen werden analog denselben Regeln hinzugefügt. Moleküle
oder Ionen mit einem ungepaarten Elektron heißen Radikale.
8) Die Anzahl der nun zu einem Element zugeordneten Valenzelektronen bestimmt auch die
Formalladung des Elements (siehe unten). Diese sollten möglichst gering sein.
Die Oktettregel:
Hauptgruppenelemente sind in ihren Verbindungen meist von insgesamt acht Valenzelektronen
umgeben (bindende und freie Elektronen). Das ist streng anzuwenden auf die Elemente der 1. und
zweiten Periode: H, He, Li, Be, B, C, N, O, F, Ne. Für die Elemente der 3. Und der folgenden
Perioden ist dies nicht durchzuhalten (hypervalente Moleküle)
34
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
b (Oktett erfüllt)
O
O
c (Oktett erfüllt)
a (Oktett erfüllt)
O
Formalladungen:
Durch homolytische Bindungsspaltung werden den Atomen, jeweils ein Elektron einer kovalenten
Bindung zugeordnet. Weicht danach diese Valenzelektronenzahl von der Hauptgruppennummer ab,
gibt man dem Atom eine Formalladung.
5 VE = HG-Nummer -1
O
O
6 VE = HG-Nummer
O
1 positive Ladung
+
-
O
7 VE = HG-Nummer +1
1 negative Ladung
O
O
Das Ergebnis der Anwendung des Valenzstrichmodells für das Ozon (O3) ist überzeugend. Das
Modell gibt unter anderem die gewinkelte Struktur von O3 wieder (kein Ring). Auch wird die
leichte Polarisierung des Moleküls (negativ an den peripheren O-Atomen, positiv am zentralen OAtom) richtig wiedergegeben.
Resonanz:
Den Regeln oben folgend kann es mehrere mögliche Valenzstrich-Formeln für ein Molekül geben.
z.B. beim O3 (Ozon) oder NCO− (Cyanat):
O
O
O
O
O
O
O
2 O
O
N
C
O
N
C
O
n
N C
m
O
2
(B)
(A + B)
2
n+m=2
Für beide Moleküle kommen je zwei Formen in Betracht (A und B). Der Pfeil
steht für die
sogenannte Resonanz (auch Mesomerie genannt). Bekannt ist dieser Begriff auch aus der
Beschreibung der Elektronenstruktur ungesättigter organischer Moleküle, wie Benzol:
(A)
(A + B)
2
(B)
H
6
H
C 1
5 C
C H
C
H
2
4 C C
H
3
H
H
6
H
C 1
5 C
C H
C
H
2
4 C C
H
3
H
(A)
H
6
H
C 1
5 C
C H
H C
2
4 C C
H
3
H
(A + B)
2
Der reale Zustand des Moleküls ist als eine Überlagerung (Mischung) der möglichen
Resonanzformen zu betrachten (keine stoffliche Mischung, sondern energetische Mischung), z.B.
beim Benzol und beim O3 in einem Verhältnis von 1:1. Daraus resultiert z.B. beim O3 eine FormalLadung von +1 am zentralen O-Atom und von −1/2 an den beiden peripheren O-Atomen. Beide OO-Bindungen sind auch gleich lang und das Molekül symmetrisch. Beim OCN− liegt keine exakte
1:1-Überlagerung vor. Weshalb nicht?).
(A)
(B)
35
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
C) Das VSEPR-Modell (Theorie der Elektronenpaarabstoßung) “valence-shell-electron-pairrepulsion“ (rein empirisch, d.h. das Modell hat keine physikalische Basis)
Regeln:
1. Bindende und freie Elektronenpaare eines Moleküls ZLn (Z = Zentralatom, L = Liganden, n =
Anzahl der Liganden) ordnen sich so um das Zentralatom an, dass sie den größtmöglichen Abstand
voneinander besitzen
2. Freie Elektronenpaare beanspruchen mehr Platz als bindende.
3. Die Raumerfüllung bindender Elektronenpaare nimmt mit steigender Elektronegativität der
gebundenen Liganden ab
4. Mehrfachbindungen brauchen mehr Platz als Einfachbindungen
Beispiele:
H
C
O
C
O
C
O
H
N
H
H
H
H
H
•
•
•
•
O
H
H
CO; Kohlenstoffmonoxid hat eine Dreifachbindung (und Formalladungen)
CO2; Kohlenstoffdioxid hat zwei Doppelbindungen und ist linear
CH4; Methan hat vier Einfachbindungen und ist tetraedrisch strukturiert
NH3; Ammoniak hat drei Einfachbindungen und ist pyramidal aufgebaut (pseudotetraedrisch); Grund: Platzanspruch des freien Elektronenpaars
• OH2; Wasser hat zwei Einfachbindungen und ist gewinkelt (pseudo-tetraedrisch) wegen
zwei freier Elektronenpaare
***************************************************************************
Beim Fluor:
F
F
oder
F
F
Ein detaillierter Blick auf die Bindungsverhältnisse: 1 × 2s- und 3 × 2p-Orbitale am F
F-F-σ-Bindung
pz-Orbitale
F
F
s-,
px- und
py-Orbitale
F
F
freie Elektronenpaare
Nach Regel 2 stossen sich die jeweils drei freien Elektronenpaare ab, was sich beim Fluor als
kleinstes Atom stark auswirkt, und zur Schwächung der σ-Bindung führt. Chlor ist wesentlich
größer (siehe Tabelle) bzw. der X–X-Abstand ist wesentlich größer. Hier führt der Platzanspruch
der freien Elektronenpaare zu keiner gegenseitigen Abstoßung.
5.2 Vorkommen, Darstellung und Verwendung
Fluor
Vorkommen in Mineralien
CaF2 = Fluorit; Na3AlF6 = Kryolith; Ca5(PO4)3F = Fluorapatit
36
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
vgl. Ca5(PO4)3OH = Hydroxylapatit; Zähnen und Knochen bestehen im Wesentlichen aus
Hydroxylapatit (+organischem „Kitt“); in den Zähnen ist teilweise OH– durch F– ersetzt; macht
Zähne härter und F− ist toxisch für Bakterien
Darstellung durch Elektrolyse von KF (in wasserfreier Flusssäure = HFa)
Verwendung:
• fluorierte organische Verbindungen (Teflon, FCKW)
• in Form von UF6 zur Anreicherung von Uran (235U)
• HF zum Ätzen von Glas
• Fluorapatit in den Zähnen
Chlor
Vorkommen: Hauptmenge gelöst im Meer; fest im Kochsalz, Meersalz; als Mineral NaCl
(Steinsalz)
Darstellung durch Elektrolyse (Chlor-Alkali-Elektrolyse):
in wässriger Lösung: Versuch: Elektrolyse von NaCl-Lösung
Cl− ½ Cl2 + e−
an der Anode
Produkte → Cl2
−
−
H2O + e
½ H2 + OH
an der Kathode
Produkte → H2, Natronlauge
Produkte → Cl2
in Schmelzen: Cl− ½ Cl2 + e−
Na+ + e− Na(s)
Produkte → Natrium
Verwendung:
• Chlorierte organische Verbindungen (PVC)
• Cl2 als Bleichmittel / Desinfektionsmittel – Versuch: Bleichen von Lackmuspapier (geht
nur in Anwesenheit von H2O): Cl2 + OH– + H2O OCl– + H3O+ + Cl–; OCl– =
Hypochlorid →oxidierende Wirkung
• Reinstsilicium aus SiCl4
• „Pyrogenes“ Kieselgel = SiO2 (als Weißpigment) aus SiCl4
Brom
Vorkommen: Hauptmenge gelöst im Meerwasser, als Mineral AgBr = Bromspat (Bromargyrit)
Darstellung durch Oxidation von Bromid mit Cl2. z.B. KBr + ½ Cl2 KCl + ½ Br2 (siehe 5.3.1)
Verwendung:
• KBr (Kaliumbromid) als Sedativum und Antikonvulsivum (Krampflöser)
• AgBr (Silberbromid) in der Fotographie
Iod
Vorkommen: Hauptmenge gelöst im Meer; NaIO3 Bestandteil des Chilesalpeters (NaNO3); als
Mineral Lautarit = Ca(IO3)2
Darstellung:
a) Oxidation von Iodiden mit Cl2 (siehe 5.3.1)
b) Reduktion von IO3−
I
2 IO3− + 6 HSO3− 2 I− + 6 SO42− + 6 H+
II
5 I− + IO3− + 6 H+ 3 I2 ↓ + 3 H2O
Verwendung:
• I2 als Antiseptikum (Iod-Tinktur)
• Iod-organische Verbindungen → organische Synthesechemie
• Thyroxin (Iod ist ein essentielles Element für den Menschen)
37
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
H
I
I
I
C
O
H
HO
I
NH2
O
C
C
HO
OH
I
I
C
C
C
C
H
I
O
C
I
C
C
C
H
C
H
NH2
H
C
C
H2
C
OH
O
Zwei Darstellungen von Thyroxin. Links eine gebräuchliche vereinfachte Darstellung, rechts eine
„vollständige“. In der vereinfachten Darstellung wird auf die Bezeichnung der C-Atome verzichtet,
sie stellen das „Gerüst“ dar. Ebenso werden diejenigen H-Atome nicht gezeigt, die ebenfalls „zum
Gerüst“ gehören und nicht Teil von Funktionellen Gruppen sind (rechts im Bild coloriert).
Thyroxin ist eine Aminosäure, ein wachstumsregulierendes Hormon und wird von der Schilddrüse
produziert. Bei Mangel versucht die Schilddrüse den Mangel durch Wachstum zu kompensieren
(→Kropfbildung)
5.3 Reaktionen und Verbindungen
5.3.1 Allgemein, die Elemente X2
Die Elemente X2 sind starke Oxidationsmittel: X2 + 2 e−
2 X− + Energie
Energie wird angegeben in Form der elektrochemischen Potentiale (E0)
X2
F2
Cl2
Br2
0
E (V)
+2,886
+1,395
+1,087
I2
+0,615
In der Reihe F > Cl > Br > I sinkt die oxidierende Wirkung
F2 oxidiert Cl−, Br−, I−
Cl2 oxidiert Br−, I−
KCl + ½ F2 KF + ½ Cl2
KBr + ½ Cl2 KCl + ½ Br2
Versuch Cl2 + 2 Br− Br2 + 2 Cl− Nachweis über die Farbe
Versuch Cl2 + 2 I− I2 + 2 Cl−
Nachweis über die Farbe
Br2 oxidiert I−
KI + ½ Br2
KBr + ½ I2
Die oxidierende Wirkung von I2 (Iod-Tinktur, -Salbe) beruht auf der Oxidationswirkung von I2
z.B. gegenüber Bakterien.
5.3.2 Reaktionen mit den Edelgasen
Edelgase IE
He > Ne > Ar > Kr > Xe > Rn
ab hier: IE > F
IE < Cl
1962 Neill BARTLETT (Vancouver):
Oxidation von Sauerstoff:
O2 + PtF6
O2[PtF6]
38
O2+ = Oxygenyl
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
Und analog von Xenon:
1962 Rudolf HOPPE (Marburg)
Xe + F2 XeF2
Xe + PtF6
„Xe[PtF6]“
„Stöchiometrie ist anders“
1962 Howard CLAASEN, John G. MALM (Argonne, US)
Xe + 2 F2 XeF4
Heute bekannt u.a.: XeF6, KrF2, XeF+, Xe2F2+, Kr2F3+, XeCl+, Xe2Cl3+
XeO2, XeO4 (= achtbindiges Xenon), HArF
5.3.3 Reaktionen mit Wasserstoff – Die Halogenwasserstoffe
X2 + H2
2 HX
Halogenwasserstoffe
Die üblichen aber trivialen Namen sind HF = Fluorwasserstoff; HCl = Chlorwasserstoff; HBr =
Bromwasserstoff und HI = Iodwasserstoff
Systematischer würde man sie als Hydrogenfluorid, -chlorid, -bromid, und -iodid bezeichnen.
Alles farblose Stoffe, mit Ausnahme des Fluorwasserstoffes HF (Sdp. 19,54°C) alle gasförmig
HX
F
–543,6
kJ
∆HB
∆HB = Bindungsenthalpie
Cl
–184,7 kJ
Br
–103,7 kJ
I
–9,46 kJ
***************************************************************************
<EXKURS: DAS CHEMISCHE GLEICHGEWICHT - DAS MASSENWIRKUNGSGESETZ>
Wir betrachten die chemische Reaktion: A + B C + D
Hinreaktion: A + B −(k1)→ C + D
k1 = Reaktionsgeschwindigkeit der Hinreaktion
Rückreaktion: C + D −(k−1)→ A + B
k−1 = Reaktionsgeschwindigkeit der Rückreaktion
a) Qualitative Beschreibung
Ein Teilchen A reagiert mit 1 Teilchen B zu 1 Teilchen C und 1 Teilchen D
Gleichzeitig: C reagiert mit D zu A und B. Im Gleichgewicht sind Hin- und Rück-Reaktion
gleich schnell (k1 = k−1) und die Teilchenzahl im System A…D ist konstant. Bei gegebenem
Volumen sind auch die Konzentrationen konstant.
Wichtig: Nach Außen hin zeigt sich bei einer chemischen Reaktion, die sich im Gleichgewicht
befindet, keine Reaktion mehr. Man muss sich aber klar machen, dass lediglich Hin- und
Rückreaktion gleich schnell ablaufen. Es ist also falsch zu sagen, die Reaktion würde aufhören.
b) Quantitativ
cC
cA
cD
= konstant = KC
cB
cA = Konzentration des Stoffs A (mol/L); cB …, cC …, cD …
KC = Gleichgewichtskonstante
KC ist typisch für eine gewählte Reaktion, hängt also von T und
p ab
Das ist das Massenwirkungsgesetz (MWG) für diese Reaktion
39
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
[C ] ⋅ [ D]
= konst = K C
andere Schreibweise: [ A] ⋅ [ B]
[C] = Konzentration des Stoffs C
Einflüsse auf die Gleichgewichtslage:
Das Prinzip des kleinsten Zwangs – LE CHATELIER (1850-1936)
Übt man auf ein im GGW befindliches System durch Änderung der äußeren Bedingungen einen
Zwang aus, so verschiebt sich das GGW derart, dass es dem äußeren Zwang ausweicht. Daraus
ergeben sich nun Möglichkeiten das GGW gezielt zu verschieben:
1) Konzentrationen
Wird die Konzentration eines Reaktanden verändert, stellt sich das Gleichgewicht neu ein.
Beispiel: Auflösen / Ausfällen von Kochsalz
NaCl(s) + n H2O Na+(aq) + Cl−(aq)
Durch Zugaben von konzentrierter Salzsäure (HCl-Gas in Wasser) gelingt es NaCl(s) auszufällen.
2) Temperatur
Durch Temperaturerhöhung wird derjenige Prozess gefördert, der Energie verbraucht.
Beispiel: Wassergas H2O + C + 129,8 kJ CO + H2
Temperaturerhöhung →
CO + H2O CO2 + H2 + 41,9 kJ
←Temperaturerniedrigung
3) Druck
Durch Druckerhöhung wird derjenige Prozess gefördert, der die kleineren (Gas)Volumina
zur Folge hat.
Beispiel: Ammoniaksynthese (NH3)
3 H2 + N2 2 NH3
Druckerhöhung →
In Wahrheit müßten für das Massenwirkungsgesetz nicht die Konzentrationen, sondern die
Aktivitäten angesetzt werden:
aA = Aktivität des Stoffs A (mol/L); aB …, aC …, aD …
aC aD
= konstant = Ka
aA aB
aA = γ . cA
γ = Aktivitätskoeffizient
Ka = Gleichgewichtskonstante
********************************************************************************
angewandt auf die Halogenwasserstoffe:
Für I2 + H2 2 HI ist ∆H = −9,46 kJ und KGGW (298 K) = 794
Bei 300°C sind 19% HI dissoziiert
Bei 1000°C sind 33% HI dissoziiert
Die Bindungen H–X bei den Halogenwasserstoffen sind kovalente Bindungen (Atombindungen).
Allerdings ist das bindende Elektronenpaar bzw. die entsprechende Elektronendichte nicht
40
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
gleichverteilt zwischen den beiden Atomen. Die beiden Bindungspartner haben eine
unterschiedliche Affinität zu Elektronen und werden dementsprechend das bindende
Elektronenpaar für sich beanspruchen. Im Beispiel das Cl-Atom mehr als das H-Atom.
Energie
Energie
Ψab
Ψab
Ψb
ΨAO
H
ΨMO
H H
Ψb
ΨAO
ΨAO
H
H
ΨMO
H Cl
ΨAO
Cl
Der beschreibende Begriff hierfür ist die Elektronegativität (EN)
********************************************************************************
<EXKURS: DIE ELEKTRONEGATIVITÄT (EN) UND WEITERE TENDENZEN IM PERIODENSYSTEM>
Elektronegativität
Die Elektronegativität ist ein Maß für die Stärke eines Atoms in einem Molekül Elektronen an sich
zu ziehen (L. PAULING). Es handelt sich bei der Elektronegativität um eine Größe, die nicht direkt
meßbar ist. Vielmehr muß sie aus verschiedenen anderen Größen wie zum Beispiel
Ionisierungsenergie, Bindungsenergie etc. gebildet werden.
Elektronegativität nach PAULING
Die Elektronegativität nimmt generell von links nach rechts und von unten nach oben zu. Bei
der Elektronegativität nach PAULING bzw. nach ALLRED und ROCHOW handelt es sich um
dimensionslose Größen, da sie bei der Einführung ihrer Skala jeweils einen Wert als Bezugsgröße
41
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
definiert haben und sich alle anderen Werte an diesem orientieren. Daneben gibt es eine Reihe
weiterer EN-Skalen. Am eingängigsten sind jedoch die Skalen nach PAULING oder ALLRED und
ROCHOW, z.B für die zweite Periode ergeben sich folgende ungefähre EN:
Li: 1,0
Be: 1,5
B: 2,0
C: 2,5
N: 3,0
O: 3,5
F: 4,0
Die Edelgase haben im Prinzip die höchsten EN (A & R): He: 5,5; Ne: 4,8; Ar: 3,2; Kr:2,9; Xe: 2,4;
Rn: 2,0
Der EN zu Grund liegen natürlich die allgemeinen Tendenzen im PSE:
Atomradien: Innerhalb einer Periode nehmen die Atomradien leicht von links nach rechts ab,
innerhalb einer Gruppe stark von oben nach unten zu. Ursache für die leichte Abnahme der
Radien innerhalb einer Periode ist die steigende effektive Kernladungszahl, die die Elektronen
zunehmend stäerker anzieht und damit die Atomradien schrumpfen läßt. Die starke Zunahme
innerhalb einer Gruppe entspricht dem „Einbau“ neuer Schalen.
Ionisierungenergien und Elektronenaffinitäten: Die Ionisierungsenergien nehmen innerhalb
einer Periode langsam zu (steigende effektive Kernladung) und weisen stets ein Maximum bei der
18. Gruppe auf (Edelgase, siehe S. 25). Innerhalb einer Gruppe nehmen die IE von oben nach
unten ab, da die Ionisierung weiter entfernter (Radius) Elektronen einfacher ist.
********************************************************************************
Im H–Cl hat Chlor eine höhere EN als Wasserstoff, also ist der Schwerpunkt der Elektronendichte
in Richtung auf das Chlor verschoben. Das wird auf folgende Weise dargestellt:
H
Cl
oder
H
δ+
Cl
δ−
Beide Darstellungsformen implizieren eine dipolare Ladungsverteilung. In der Tat sind HXMoleküle Dipole.
Definition Dipol: Molekül, das sich im elektrischen Feld orientiert (es hat ein Dipolmoment)
Ein weiterer „Beweis“ für die oben beschriebene Ladungsverteilung ist die charakteristische
Reaktion der HX-Verbindungen mit Wasser:
HCl-Gas ist in Wasser löslich, zusätzlich reagiert es nach
HCl + H2O
H3O+ + Cl–
H3O+ = Oxonium- / Hydronium-Ion
HX in Wasser sind Säuren – Die Lösung von HCl-Gas in Wasser nennt man Salzsäure
********************************************************************************
<EXKURS: SÄUREN UND BASEN>
1) Säuren und Basen - Verschiedene Definitionen
42
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
ARRHENIUS: Säuren dissoziieren in Wasser unter Bildung von H+-Ionen, Basen unter Bildung von
OH–
z.B. HCl(g) (in H2O) → H+ + Cl–
NaOH(s) (in H2O) → Na+ + OH–
BRÖNSTEDT: Säuren sind Protonendonatoren, Basen sind Protonenakzeptoren
Es gibt nur eine Säure, wenn auch eine Base zugegen ist:
HA + B A– + BH+
Säure HA + Base B korrespondierende Base A– + korrespondierende Säure HB+
Wichtig: Bezugspunkt H+-Ion (bzw. H3O+)
LEWIS: Eine LEWIS-Säure ist ein Teilchen mit einem Elektronenmangel, LEWIS-Base ist ein
Teilchen mit einem Elektronenüberschuss.
Beispiele für Lewis-Säuren und -Basen:
1) Das Proton (H+) ist eine Lewis-Säure (und auch eine Brönstedt-Säure), Wasser ist eine LewisBase (= Brönstedt-Base) (links). Wasser ist aber auch eine Brönstedt-Säure, allerdings keine LewisSäure (rechts) !!!
H
O
H+ +
H
+
O
H
H
O
bzw.
H
H
O
+
H
H
H
O
H
H
-
+
+
H
O
H
2) BF3 ist eine Lewis-Säure, NH3 eine Lewis-Base
H
F
F
B
F
+
H
N
H
F
H
B
N
F
H
H
F
3) Cu2+-Ion in wässriger Lösung = Cu2+(aq)
OH2
H2O
2+
OH2
Cu
H2O
OH2
OH2
Cu2+-Ion ist eine Lewis-Säure, OH2-Molekül ist eine Lewis-Base
Fazit: Das Elegante an der LEWIS-Definition ist, dass diese sowohl die BRÖNSTEDT’schen Säuren
und Basen mit einschließt sondern darüber hinaus ein (einfaches) Modell für die
Bindungsverhältnisse in Komplexen (Koordinationsverbindungen) liefert. In wässrigen Lösungen
ist die BRÖNSTEDTsche Definition ausreichend.
43
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
2) Säuren und Basen in Wasser – Die Säurestärke – Die Basenstärke
Allgemein gilt für eine Säure in Wasser:
HA + H2O
+
−
H3O + A
c (H3O+) c (A−)
= konstant
c (HA) c (H2O)
das MWG:
dabei sind die Konzentration von Wasser = c(H2O): 1 l Wasser = 1000 g (bei 25°C)
und das Molgewicht MG(H2O) = 18,015 mol/l; 1000 g H2O ≈ 55,5 mol
Geht die Konzentration von Wasser in die Konstante mit ein entsteht die Säurekonstante KS
c (H3O+) c (A−)
= KS
c (HA)
= Säurestärke
←

→

KS groß;
GGW
H3O+ + A− vollständig (weitgehend dissoziiert)
⇒ starke Säure (z.B. Salzsäure)
←

→
KS klein;
GGW HA + H2O
wenig dissoziiert
⇒ schwache Säure (z.B. Essigsäure)
Analog für eine Base (A−)
c (OH−) c (HA)
= KB
c (A−)
= Basenstärke
starke Base:
OH− (z.B. aus NaOH in H2O = Natronlauge)
schwache Base:
NH3 (Ammoniak)
sehr schwache Base: F− (aus KF in H2O)
3) Reines Wasser - Der pH-Wert
H2 O + H2 O
H3O+ + OH– Autoprotolyse-Gleichgewicht
experimenteller Beweis: Leitfähigkeit von reinstem Wasser
MWG:
bzw.
c (H3O+) c (OH−)
c (H3O+) c (OH−)
= KS(H2O) = 1,8.10−16
= konstant
c (H2O)
c (H2O) c (H2O)
c(H3O+) . c(OH–) = KS (H2O) . c(H2O) = KW = 10–14 = Ionenprodukt des Wassers
KS = Säurekonstante von Wasser, KB = Basenkonstante von Wasser und KS . KB = KW
weil: c(H3O+) = c(OH−), ist c(H3O+) = c(OH–) = 10–7 (in reinem Wasser bei 25°C)
Da dies recht unhandliche Größen sind, werden c(H3O+), Ks, Kw, KB durch ihre negativen
dekadischen Logarithmen ersetzt:
→
pH
pK S
pK B
pK W
= – log c(H3O+)
= – log KS
= – log KB
= – log KW
44
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
pH von reinem Wasser = 7. Es gilt KS . KB = KW und pKS + pKB = pKW = 14
4) Korrespondierende Säure- und Basepaare
Beispiele
Säure
pKS
korrespondierende Base
pKB
−
Salzsäure*
Cl
+
H2O
H3O
15,74
−1,74
2−
Phosphorsäure
2,12
11,88
H2PO4
Ameisensäure
2,75
Formiat
11,25
Essigsäure
4,75
Acetat
9,25
9,25
NH3
4,75
NH4+
−
H2O
15,74
OH
−1,74
*Salzsäure ist vollständig dissoziiert, d.h. es ist eine stärkere Säure als H3O+. Deshalb kann in
wässriger Lösung kein pKS angegeben werden
⇒ zu einer starken Säure korrespondiert immer eine schwache Base und andersherum. pKS +
pKB = pKW = 14
5) Bedeutung des pH-Werts (bzw. Konzentration von H3O+)
•
•
•
Biologie / Biochemie: viele Reaktionen sind vom pH-Wert der Umgebung abhängig z.B.
Nährstoffaufnahme
Organische Chemie / Anorganische Chemie: Verbindungen und dissoziierte Protonen sind
in ihren Eigenschaften (Reaktivität, Farbe, u.a.) vom pH-Wert abhängig.
Bioanorganische Chemie: Mineralisierung oder Verfügbarkeit von Metallionen sind vom pH
abhängig
6) Messung des pH-Werts
a) mit pH-Indikatoren
Indikatoren (Farbindikatoren): Organische oder anorganische Moleküle, die schwache Säuren sind
und daher als protonierte (HInd) und deprotonierte Form (Ind‒) existieren und für beide Formen
unterschiedliche Farben zeigen.
HInd + H2O
MWG:
Ind− + H3O+
c (H3O+) c (Ind−)
= KS(Indikator)
c (HInd)
bzw.
c (H3O+) =
KS(Ind) ist klein (schwache Säure)!!!
gebräuchliche Indikatoren:
Indikator
Methylrot
p-Nitrophenol
Bromthymolblau
Phenolphthalein
Lackmus
Umschlagsbereich
4,4 – 6,2
5,0 – 7,0
6,2 – 7,6
8,0 – 10,0
4,5 – 8,3
45
Farbumschlag
rot – gelb
farblos – gelb
gelb – blau
farblos – rot
rotviolett - blau
KS(Ind) c (Ind−)
c (HInd)
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
Versuche - Bespiele für Indikatoren:
-Phenolphthalein
-Blaukraut
-Universalindikator
-Kölsches Leitungs-Wasser
Weshalb tritt hier ein Umschlagbereich auf, und kein „scharfer“ pH-Wert?
aus
+
c (H3O ) =
KS(Ind) c (Ind−)
ergibt sich
c (HInd)
c (Ind−)
pH = pKS(Ind) + log
c (HInd)
Ist die Unterscheidbarkeit der Farben von HInd und Ind− beispielsweise erst gegeben, wenn
c(HInd)/c(Ind−) = 10/1 oder 1/10 ist, dann ist der Umschlagsbereich pH = pKS(Ind) ±1
Universalindikatorpapier wird durch Mischen mehrerer Indikatoren so präpariert, dass es den
gesamten pH-Bereich überstreicht.
b) Messen des pH-Wertes mit der pH-Elektrode
Das elektrochemische Potential der Reaktion
1/2 H2 + H2O
H3O+ + e−
hängt von c(H3O+) ab. Also lässt sich bei standardisierten Bedingungen (p, T, c(H2)) anhand eines
gemessenen Potentials der pH-Wert ermitteln (siehe dazu EXKURS REDOXREAKTIONEN)
c) Leitfähigkeit
Durch Leitfähigkeitsmessungen kann man grundsätzlich die Art und Anzahl von Ionen in einer
Lösung bestimmen. Daher auch die c(H3O+).
7) Neutralisationsanalyse
Zur Bestimmung des Gesamtgehaltes (Anzahl der Teilchen) einer Lösung an H3O+-Ionen titriert
man mit Lösungen bekannten OH−-Ionen-Gehalts (und umgekehrt). Die Neutralisationsreaktion ist
exotherm:
H+ + OH− H2O
| ∆H = −57,3 kJ/mol
oder
H3O+ + OH− H2O + H2O
Der Endpunkt der Titration (das dosierte
Zutropfen einer sogenannten Maßlösung) ist
erreicht, wenn die zugegebene Menge Base
(Säure) der vorliegenden Menge Säure (Base)
entspricht (= Äquivalenzpunkt). Der
Äquivalenzpunkt kann durch Umschlag eines
Indikators oder mittels pH-Elektrode oder
Leitfähigkeit ermittelt werden.
46
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
pH = pKS(Ind) + log
c (Ind−)
c (HInd) , d.h. in einer Säurelösung liegt
Für den Umschlag des Indikators gilt:
anfänglich Hind vor. Im Verlauf der Titration wird die zu analysierende Säure verbraucht und
schließlich auch Hind, welches am Äquivalenzpunkt dann halb und nur bei wenig mehr Base
vollständig zu Ind− deprotoniert ist.
Beispiel 1 Titration einer starke Säure mit starker Base (Salzsäure + Natronlauge)
H3O+(aq) + Cl–(aq)
a) HClgas + H2O
b) NaOHfest + H2O
OH–(aq) + Na+(aq)
c) H3O+(aq) + Cl–(aq) + OH–(aq) + Na+(aq)
2 H2O + Na+(aq) + Cl–(aq)
= Lösung von Kochsalz (NaCl) in Wasser; pH = 7; Indikator: Bromthymolblau
Beispiel 2 Titration einer schwachen Säure mit starker Base (Essigsäure + Natronlauge)
= Lösung von Natriumacetat in Wasser
H3O+(aq) + Ac–(aq)
a) HAc + H2O
b) NaOHfest + H2O
Ac = Acetat = CH3COO–
OH–(aq) + Na+(aq)
c) H3O+(aq) + Ac–(aq) + OH–(aq) + Na+(aq)
2 H2O + Na+(aq) + Ac–(aq)
Wichtig: Bei der Neutralisationsreaktion spielt die Stärke der Säure nun keine Rolle. Durch die
starke Base wird die Säure vollständig dissoziiert und alle H3O+ werden neutralisiert. Aber: eine
schwache Säure hat eine starke Base als korrespondierenden Partner. Acetat ist eine Base, die
resultierende Lösung von Natriumacetat ist also basisch:
–
d) Ac (aq) + H2O
–
HAc + OH (aq)
c (HAc) c (OH−)
KB(Ac−) =
c (Ac−)
mit c(HAc) = c(OH–) ist
c (OH−)2
KB(Ac−) = c (Ac−)
und mit KW2 = c(H3O+)2 · c(OH–)2
KB(Ac−) =
+ 2
c(H3O
) =
und daraus:
KW 2
KB(Ac−) c (Ac−)
KW2
c (H3O+)2 c (Ac−)
c (H3O+) =
bzw.
KW 2
KB(Ac−) c (Ac−)
Mit KS(HAc) · KB(Ac–) = KW (gilt für alle korrespondierenden Säure-Base-Paare)
c (H3O+) =
wird daraus:
KW KS(HAc)
c (Ac−)
oder: pH = 7 + 1/2 pKS(HAc) + 1/2 log c(Ac–)
47
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
Indikator: Phenolphthalein
Beispiel 3 Titration einer schwachen Base mit starker Säure (Ammoniak + Salzsäure)
Betrachtet man die vorhergehenden Beispiele, wird klar, dass die resultierende Lösung identisch ist
mit einer Ammoniumchlorid-Lösung in Wasser. Nachdem Ammoniak eine schwache Base ist, ist
klar, dass Ammonium-Lösungen sauer reagieren:
Für NH4+(aq) + H2O
H3O+(aq) + NH3 gilt
KS(NH4+) =
und mit c(NH3) = c(H3O+) ist
c (NH3) c (H3O+)
c (NH4+)
c (H3O+)2
KS(NH4+) =
c (NH4+)
daraus wird c(H3O+)2 = KS(NH4+) . c(NH4+) bzw.
c (H3O+) =
KS(NH4+) c (NH4+)
und mit KS(NH4+) · KB(NH3) = KW
KW c (NH4+)
KB(NH3)
c (H3O+) =
wird daraus:
oder: pH = 7 – 1/2 pKB(NH3) – 1/2 log c(NH4+)
Beispiel 4 Titration einer schwachen Base mit schwacher Säure (Ammoniak + Essigsäure)
Die nach der Titration erhaltene Lösung ist identisch mit einer Lösung von Ammoniumacetat in
Wasser. Ammonium reagiert in Wasser sauer, Acetat hingegen basisch, ob die resultierende Lösung
insgesamt sauer oder basisch ist, hängt von KS(Säure) und KB(Base) ab:
Für NH4+(aq) + H2O
KS(NH4+) =
gilt
c (NH3) c (H3O+)
c (NH4+)
mit c(Ac−) = c(NH4+) ist
ist
und Ac−(aq) + H2O
H3O+(aq) + NH3
KB(Ac−) =
und
KS(NH4+) =
c (HAc) c (OH−)
c (Ac−)
c (NH3) c (H3O+) KB(Ac−)
c (OH−) c (HAc)
c (NH3) c (H3O+) KB(Ac−) c (H3O+)
KS(NH4+) =
KW c (HAc)
c (H3O+)2 =
umgeformt:
KS(NH4+) KW c (HAc)
c (NH3)
KB(Ac−)
OH−(aq) + HAc
c (Ac−) =
c (HAc) c (OH−)
bzw.
KB(Ac−)
c (OH−) =
und mit
KW
c (H3O+)
c (H3O+)2 KB(Ac−) c (NH3)
=
c (HAc)
KW
und da NH3 und HAc in äquivalenten Mengen
eingesetzt wurden c(HAc) = c(NH3)
48
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
gilt
c (H3O+) =
KS(NH4+) KW
KB(Ac−)
gilt
c (H3O+) =
KS(NH4+) =
und mit
KS(HAc) KW
KB(NH3)
KW
KB(NH3)
KB(Ac−) =
,
sowie
KW
KS(HAc)
oder
pH = 7 + 1/2 pKS(HAc) – 1/2 pKB(NH3)
8) Puffer
Puffer sind Systeme aus schwachen Säuren und deren korrespondierenden Basen, die H3O+-
c (H3O+) = KS c (HA)
c (A−)
Konzentration ergibt sich dabei aus:
Säurezugabe:
H3O+ + A– → HA
verschiebt nur unwesentlich das Gleichgewicht
Basenzugabe:
OH– + HA → A–
verschiebt nur unwesentlich das Gleichgewicht
Bei einer 1:1-Verhältinis von c(HA) und c(A–) ist pH = pKS(HA)
Bei einem Verhältnis c(HA)/c(A–) von 10/1 steigt der pH nur um 1;
Bei einem Verhältnis c(HA)/c(A–) von 100/1 steigt der pH nur um 2
Pufferlösungen bieten stabile pH-Verhältnisse für Reaktionen, die empfindlich auf Änderung des
c(H3O+) reagieren. Viele biochemische Prozesse sind darunter.
9) der pH-Wert von Elektrolyten
Wie in 7) erläutert weißen die wässrigen Lösungen diverser Salze teilweise pH-Werte = 7 auf.
Vorraussetzung dafür ist, dass ein oder beide Ionen (Kation und/oder Anion) Säuren oder Basen
sind, mit H2O reagieren. In erweitertem Sinne gilt dies für wässrige Lösungen jeglicher Stoffe, die
mit H2O als Säuren oder Basen reagierten können. Neben den Elektrolyten (anorganische Salze)
können dies auch organische Moleküle sein (Carbonsäuren, Alkohole, Amine, Amide …). Der pHWert läßt sich rechnerisch wie in 7) gezeigt ermitteln.
Versuche - Bespiele für den pH von Elektrolyten (Nachweis mit pH-Papier):
- primäres Phosphat z.B. NaH2PO4 (sauer)
- sekundäres Phosphat z.B. Na2HPO4 (leicht sauer)
- tertiäres Phosphat z.B. Na3PO4 (basisch)
********************************************************************************
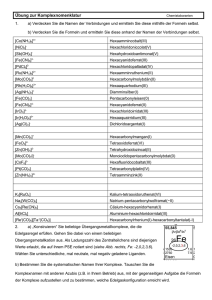
Die Säurestärke der Halogenwasserstoffe: (vergleichbar nicht in Wasser, sondern etwa in
Essigsäure):
HI > HBr > HCl > HF; Grund (vereinfacht): zunehmende Bindungsstärke H–X
49
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
5.3.4 Die Silberhalogenide
Die Verbindungen AgX (außer AgF) sind sehr schwerlösliche Festkörperverbindungen. Die
Schwerlöslichkeit wird zu analytischen Zwecken genutzt.
********************************************************************************
<EXKURS: DIE LÖSLICHKEIT - DAS LÖSLICHKEITSPRODUKT>
Elektrolyte: Stoffe, die beim Auflösen in Wasser solvatisierte Ionen bilden und sich dadurch lösen.
E. lassen sich beschreiben als im Festkörper aus Ionen aufgebaute Stoffe (Ionenbindung). Man
nennt sie auch Salze oder salzartige Stoffe.
Beim Auflösen eines Elektrolyten löst sich der Gitterverband der Anionen und Kationen auf und es
bilden sich solvatisierte Ionen. Während das Auflösen des Gitterverbandes normalerweise
endotherm ist (Gitterenergie) ist die Bildung der solvatisierten Ionen exo- oder endotherm
(Solvatationsenergie). Letzteres ist of entscheidend ob sich ein Stoff löst oder nicht (siehe Kapitel
2).
Das Ausfallen eines Elektrolyten erfolgt dann, wenn seine Löslichkeit überschritten ist.
Versuche - Bespiele für ausfallende Festkörper (Salze):
1) CuSO4 in H2O = Cu2+(aq) + SO42‒(aq);
Kupfersultat CuSO4 löst sich recht gut in
Wasser, bei Zugabe von Ammoniak (Base: NH3 + H2O = NH4+ + OH‒) fällt Cu(OH)2 aus:
Cu2+(aq) + 2 OH‒(aq) Cu(OH)2 ↓
Der ↓ bedeutet, der Stoff fällt aus.
Wiederauflösen von Cu(OH)2 (Teilen der Suspension):
a) durch Säure: in saurer Lösung gibt es nicht genügend OH‒-Ionen. Bzw. die OH‒-Ionen
des Feststoffs reagieren als starke Basen gegenüber Säure.
b) durch Ammoniak: Cu2+ bildet einen Komplex [Cu(NH3)4(H2O)2]2+, der
thermodynamisch gesehen günstiger/stabiler ist als Cu(OH)2.
2) BaCl2 in H2O = Ba2+(aq) + 2 Cl‒(aq); Bariumchlorid ist in Wasser recht gut löslich, bei
Zugabe von Natriumsulfat-Lösung (= 2 Na+(aq) + SO42‒(aq)) fällt BaSO4 (Bariumsulfat) aus:
Ba2+(aq) + SO42‒(aq) BaSO4 ↓
BaSO4 lässt sich nicht durch Säuren auflösen. SO42‒ ist keine Base.
Das Massenwirkungsgesetz MWG für den Lösungsvorgang eines Elektrolyten stellt sich wie
folgt dar:
Beispiel Silberhalogenide AgX: AgX(fest)
AgX(gelöst)
Ag+(aq) + X−(aq)
c (Ag+) c (X−)
= konstant
c (AgXgelöst)
MWG (nur für das zweite Gleichgewicht*:
(* das ist der Trick daran)
Wichtig: c(AgXgelöst) ist die Konzentration von gelösten AgX-Molekülen in der Lösung. Bei einem
schwerlöslichen Stoff ist diese Konzentration sehr gering. Bei vielen Elektrolyten geht man davon
50
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
aus, dass es solche Moleküle nicht gibt sondern diese Verbindungen nur im Festkörper existieren.
Ungeachtet dessen ist c(AgXgelöst) eine vernünftige Rechengröße und am wichtigsten: Diese Größe
ist konstant: AgX-Teilchen in Lösung solvatisieren sich und bilden Ionen und in gleichem Maße
werden AgX-Teilchen aus dem Festkörper nachgeliefert. Ob es nun also solche Teilchen gibt oder
nicht, ihre Konzentration ist in einer Lösung, bei der zur gleichen Zeit ein Bodenkörper (Festkörper)
vorliegt konstant.
Dann wird aus dem MWG:
c(Ag+) · c(X−) = KL = Löslichkeitsprodukt
Allgemein gilt für die Auflösung eines Elektrolyten: KmAn
KL = c(Kn+)m c(Am−)n
m Kn+ + n Am−
Und für die Löslichkeit L
L=
n+m
KL
n mm
n
KL = (dimensionslose Größe); L = Löslichkeit (in g/l)
⇒ pKL = − log KL
Beispiel 1 Die Löslichkeit der Silberhalogenide:
AgX
pKL
AgF
–2,3
AgCl
9,96
AgBr AgI
12,4 16
Löslichkeit von Silberchlorid (AgCl; MG =143,32 g/mol):
AgCl löst sich auf unter Bildung von Ag+ und Cl– zu gleichen Teilen. Deshalb ist
c(Ag+) = c(Cl−) = L;
Aus der Formel: L = (KL)1/2 mit KL = 1,09 · 10–10 (Tabellenwert)
c(AgClgelöst) = (1,09 · 10–10)1/2 = 1,0471 · 10–5 (mol/l); Löslichkeit = 1,0471 · 10–5 × 143,32 =
1,5 mg in 1000 ml Wasser
Löslichkeit von Silberfluorid (AgF; MG = 126,87 g/mol):
L = (KL)1/2 = 1800 g in 1000 ml Wasser
Beispiel 2 Die Löslichkeit von Bleichlorid (PbCl2; MG = 278,096 g/mol):
KL = c(Pb2+) · c(Cl–)2 = 2 · 10–5 (pKL = 4,77)
Wenn 1 Teilchen PbCl2 sich auflöst, entstehen 1 Teilchen Pb2+ und 2 Teilchen Cl–,
deshalb ist c(Pb2+) = L, c(Cl–) = 2 L
daraus leitet sich ab KL = c(Pb2+) · {2 c(Pb2+)}2 = {4 c(Pb2+)}3 und L = c(Pb2+) = (KL/4)1/3
und andererseits KL = 1/2 c(Cl–) · c(Cl–)2 = {1/2 c(Cl–)}3 und L = 1/2 c(Cl–) = (KL/4)1/3
dasselbe aus der Formel: L = (KL/4)1/3 = 1,71 · 10–2 (mol/l), bzw. 4,755 g/l
Weshalb lösen sich manche Stoffe und andere sind „unlöslich“? (Ein didaktischer Ausflug)
Es gibt darauf drei verschiedene Antworten:
1) Die Antwort aus dem Löslichkeitsprodukt (tabellierte Werte):
51
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
Ein Stoff mit einem kleinen Löslichkeitsprodukt KL ist schlecht löslich, ein Stoff mit einem großen
Löslichkeitsprodukt ist gut (oder leicht) löslich. Oder: Ein Stoff mit einem großen pKL-Wert ist
schwer löslich, ein Stoff mit einem kleinen pKL-Wert ist gut löslich, Stoffe mit negativem pKL-Wert
sind sehr gut löslich (vgl. Tabelle).
KL
pKL
KL
pKL
Na2SO4
AgF
200
30,60
−2,3
−1,48
−5
NaCl
38
CaSO4
4,62
−1,58
2,4 · 10
−5
−7
BaF2
4,62
SrSO4
6,12
2,4 · 10
7,6 · 10
−5
−9
4,77
BaSO
8,82
PbCl2
1,60 · 10
1,5 · 10
4
−10
−22
AgCl
9,72
ZnS
21,60
1,09 · 10
2,5 · 10
−11
−28
CaF2
10,41
CdS
28,00
3,9 · 10
1,0 · 10
−18
−54
17,96
HgS
53,80
Hg2Cl2
1,6 · 10
1,10 · 10
−14
• CdS in Wasser hat eine Löslichkeit 10 mol/l; bei einem Molgewicht von 144,477 g/mol
ist die Löslichkeit 1,4·10−12 g/l, das sind 1,4 pg (Pikogramm/l).
• Für HgS sind das 1,26·10−27 mol/l. Auf den ersten Blick ist damit erkennbar, dass bei der
Avogadrokonstante NA = 6,022·1023 mol−1 die Chance ein Hg2+-Ion in einem Liter einer
solchen Lösung zu finden kleiner als 1:1000 liegt.
• Die Löslichkeit von NaSO4 hängt stark von der Temperatur ab, bei 25°C lösen sich 280 g/l
H2O (MG = 142,04) = 1,97 mol/l; mit L = (KL/4)1/3 ist KL = 4 · (1,97)3 = 30,58
Bleibt die tiefergehende Frage, weshalb gibt es solche Unterschiede?
2) Antwort aus der Thermodynamik (vgl. Kapitel 2): Bei der Auflösung eines Elektrolyten kommt
es zur Auflösung des Kristallverbandes (Verlust an Gitterenthalpie) unter Bildung von solvatiierten
Ionen (Gewinn an Solvatationsenthalpie)
Energie
Energie
M+g
∆HHydr
+
M+g + X−g
X−g
Ionen in der Gasphase
∆HHydr
∆HGitter
Ionen in der Gasphase
M+Hydr.
∆HGitter
Festkörper
X−Hydr.
in Lösung
Festkörper
∆HLösung
(MX)s
in Lösung
M+Hydr.
(MX)s
∆HLösung
X−Hydr.
Versuche: Auflösen von CaCl2 in Wasser: Wasser erwärmt sich; Auflösen von NH4NO3 in
Wasser: Wasser kühlt ab.
Solvatisierte Ionen (in Wasser: aquatisierte Ionen):
OH2
OH2 H O
2
OH2 Cl H2O
OH2
H2O
OH
2 H2O
H2O
H2O
Na+
OH2
= Na+aq Cl-aq = aquatisierte Ionen
Ion-Dipol-Wechselwirkungen zwischen dem Dipol Wasser und den Ionen (→ Gewinn an
Solvatationsenthalpie)
52
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
Bleibt wiederum die Frage, kann man das verstehen oder gar vorraussagen? Welche Parameter
bestimmen denn die Gitterenergie und die Hydratisierungsenthalpie?
3) Antwort aus den Ionenradien, Hydratisierungsenthalpie und dem HSAB-Konzept
a) Die Hydratisierungenthalpie sollte (in erster Näherung) mit steigendem Ionenradius größer
werden (mehr H2O haben Platz um das Kation oder Anion).
b) Die Gitterenergie ist in vereinfachter Weise eine Funktion der Ionenradien:
Coulombsche
Energie:
1
n+e+ n−e−
E=
4π ε0 r2
e+, e− Elementarladungen, n+, n− Anzahl der
Elementarladungen,
r = Abstand zwischen den beiden Ionen,
ε0 ist die elektrische Feldkonstante.
Wenn in erster Näherung die Coulombsche Energie der Gitterenthalpie entspricht, dann steigt die
Gitterenthalpie mit steigender Ladung und sinkt mit der Größe der Ionen. Das könnte den
Unterschied zwischen NaF und CaF2 erklären, stimmt aber nicht mit dem Lösungs-Verhalten von
AgF und AgCl überein.
Die Coulombsche Näherung ist also zu grob, was zu erwarten war, berücksichtigt sie doch nicht den
kovalenten Teil der Bindung in solchen Salzen. Tatsächlich ist die Annahme von rein ionischer
Bindung selbst für ausgeprägte Salze wie NaCl eine recht schlechte Näherung und Kovalenz spielt
eine wichtige Rolle (dazu später mehr).
Wie ist nun aber die kovelente Wechselwikrung zwischen den Anionen und Kationen
abzuschätzen? Dazu hilft das HSAB-Konzept.
c) Das HSAB-Konzept (principle of hard and soft acids and bases) sagt, dass die
Wechselwirkungen zwischen harten Lewis-Säuren und harten Lewis-Basen sowie zwischen
weichen Lewis-Säuren und weichen Lewis-Basen stabiler sind als die Kombination hart-weich.
• Harte Lewis-Säuren sind kleine, möglichst hochgeladene Kationen (H+ oder H3O+, Na+,
Be2+, Al3+, Fe3+...).
• Harte Lewis-Basen sind kleine, hochgeladene Anionen (O2−, OH−, F−, Cl− ...).
• Weiche Lewis-Säuren sind große, möglichst niedrig geladene Kationen (Cu+, Cu2+, Pd2+,
Tl+, Hg2+, ... ).
• Weiche Lewis-Basen sind große, möglichst niedrig geladene Anionen (S2−, HS−, Br−, I−, ... )
Häufig wird auch der Begriff „polarisierbar“ diskutiert. Weiche Säuren und Basen sind leicht
polarisierbar, d.h. ihre Ladung ist über einen großen Bereich verteilt und lässt sich leicht
„umverteilen“, harte Säuren und Basen sind schwer polarisierbar.
Wichtig: das HSAB-Konzept ist sehr empirisch und nie absolut: z.B. ist Fe2+ sicher weicher als Fe3+
(kleiner und höher geladen) und Cu2+ ist weicher als Fe2+ (weil größer). Schwierig wird es bei Na+
und Ca2+ (höher geladen, aber deutlich größer) ...
Im Hinblick auf die Löslichkeit, sagt das HSAB-Konzept. Salze die eher einer hart-hart oder weichweich-Kombination entsprechen haben hohe Gitterenergien als die mit einer hart-weichKombination. In der obigen Tabelle lässt sich daher verstehen weshalb NaCl vs. AgCl eine deutlich
53
ALLGEMEINE CHEMIE FÜR STUDIERENDE DER NATURWISSENSCHAFTEN
IM WS 2012/2013
geringere Gitterenergie aufweist und in der Serie ZnS, CdS und HgS die Gitterenergie
offensichtlich dramatisch ansteigt.
Nochmal zusammenfassend:
Das Ausfallen eines Elektrolyten erfolgt dann, wenn seine Löslichkeit bzw. das
Löslichkeitsprodukt überschritten ist. Kurz vor dem Ausfallen nennt man eine Lösung gesättigt,
nach Überschreiten der Löslichkeit nennt man die Lösung übersättigt, es setzt dann die
Kristallisation des übersättigten Stoffes ein (Ausfallen oder Kristallisieren).
Übersättigung herbeiführen (zum Zwecke des Ausfällens eines Stoffes) kann man durch.
1)
2)
3)
4)
Zugabe einer Komponente (Anion oder Kation) des Stoffes.
Temperaturerniedrigung
Volumenreduktion (Verdampfen des Lösungsmittels)
Verschlechterung des Lösungsmittels (z.B. Mischen von H2O mit Ethanol)
Ist ein Stoff ausgefallen, kann er i.A. durch Filtration von der Lösung getrennt werden. In der
Lösung bleiben alle weiteren (an der Fällung unbeteiligten) Ionen gelöst und können so vom
gefällten Stoff abgetrennt werden. Je nach Löslichkeit des Stoffes bleiben aber auch einige der
Ionen in Lösung, die den Stoff aufbauen. Z.B. in einer Lösung aus der AgCl ausgefallen ist, lassen
sich immer noch Cl‒ und Ag+ Ionen finden, in einer Lösung aus der HgS ausgefallen ist, jedoch
schwerlich Hg2+ und S2‒ Ionen (siehe obige Tabelle).
Auch hat die Löslichkeit Implikationen auf die Giftigkeit eines Stoffes. Um physiologischen
Schaden (Giftwirkung) anzurichten muss ein Stoff nämlich löslich sein. Beispielsweise sind Ba2+Ionen giftig (Barium ist ein Schwermetall), in gegenwart von SO42‒-Ionen fällt BaSO4 aus und die
restlichen Ba2+-Ionen in einer solchen Lösung sind zu wenige, als dass sie eine Giftwirkung
entfalten könnten. Daher werden Suspensionen von BaSO4 als Kontrastmittel für
Röntgenuntersuchungen des Gastro-Intestinal-Traktes verwendet. Selbst im Magen (stark sauer) ist
BaSO4 kaum löslich.
********************************************************************************
Die Löslichkeit der Alkalimetallhalogenide (NaX und KX) ist sehr viel größer als die der AgX.
Kochsalz (NaCl) und Sylvit (KCl) werden aus Gesteinen ausgeschwemmt und finden sich in
gelöster Form in großen Mengen im Meer. Dabei tritt Natrium 30x häufiger auf als Kalium
(weshalb wohl?).
54