Nichtlineare Bauelemente

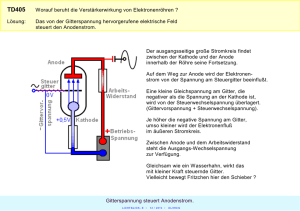
Theorie zum Versuch nicht Lineare Bauelemente im MET-Labor
1 Theorie zum Versuch Nichtlineare Bauelemente im Labor-MET
In diesem Dokument soll kurz auf den Aufbau und die Funktionsweise von Elektronenröhren am
Beispiel der Elektronenröhre EF 98 eingegangen werden.
1.1 Aufbau der Elektronenröhre EF 98
In Bild 1.1 wird der Aufbau der Elektronenröhre EF 98 in schematischer Weise dargestellt. Die Röhre
EF 98 besitzt fünf Elektroden. Aus diesem Grund gehört die EF 98 zur Gruppe der Pentoden. Der
Begriff Pentode leitet sich aus dem griechischen Zahlwort Penta ab, welches für die Zahl 5 steht. Die
Anschlusskontakte der Röhrenheizung stellen keine Elektroden in diesem Sinne dar.
Bezeichnungen der einzelnen Anschlüsse:
• a : Anode
• g3 : Bremsgitter
• g2 : Schutzgitter
• g1 : Steuergitter
• k : Kathode
• f : Heizung
Abbildung 1.1: Symbolbild einer Pentode mit Elektrodenbezeichnungen
Funktionsweise: Die Kathode (k) der EF 98 wird durch einen gesonderten und elektrisch von der
Kathode isolierten Heizstromkreis (f) erhitzt. Als Kathode wird immer die Elektrode eines Systems
bezeichnet, welche dem System Elektronen zuführt. Daher muss immer der Minuspol der Gleichspannungsquelle an der Kathode angeschlossen werden. Der Pluspol der Gleichspannungsquelle wird mit
der Anode verbunden.
Damit Elektronen einen metallischen Leiter verlassen können müssen Sie eine gewisse Austrittsarbeit
leisten. Bei einem kalten metallischen Leiter ist die Austrittsarbeit der Elektronen für das Verlassen
des Leiters im Allgemeinen zu hoch. Man kann den Elektronen den Austritt aus dem metallischen
Leiter durch Erhitzen des Leiters erleichtern. Dadurch reduziert man die noch notwendige Austrittsarbeit der Elektronen durch Zuführung von thermischer Energie. Je höher die Kathodentemperatur
ist, desto leichter können die Elektronen die Kathode verlassen. Die ausgetretenen Elektronen bilden
eine Raumladungswolke um die Kathode herum. Hebt man nun die Anode in Bezug auf die Kathode
auf ein positives Potential an, so bildet sich in der Röhre ein elektrisches Feld zwischen der Anode und
der Kathode aus. Dieses elektrische Feld zieht die Elektronen der Raumladungswolke in Richtung der
Anode, da Elektronen in einem elektrischen Feld immer zum positiveren Pol gezogen werden.
1.2 Die Wirkungsweise des Steuergitters
Durch das Einbringen eines Steuergitters g1 gemäß Bild 1.1 wird die Elektronenröhre steuerbar. Das
Steuergitter erhält eine in Bezug auf die Kathode negative Spannung. Damit wird nun die Verteilung
Dipl.-Ing.(FH) Thomas Peschko
1 von 5
Theorie zum Versuch nicht Lineare Bauelemente im MET-Labor
des elektrischen Feldes in der Röhre beeinflusst. Ist die negative Spannung Ug1 am Gitter g1 negativ
genug, dann werden die Elektronen zwischen der Kathode und dem Gitter g1 vom Feld der Anode
abgeschirmt. Der Elektronenstrom kommt zum Erliegen. Wird die Spannung Ug1 nun wieder weniger
negativ, so werden wieder einige Elektronen zwischen der Kathode und dem Gitter g1 vom elektrischen
Feld der Anode erfasst. Es beginnt ein Elektronenstrom zu fließen. Je weniger negativ die Spannung
Ug1 am Gitter g1 ist, desto größer wird der Anodenstrom Ia . Eine gegenüber der Kathode positive
Spannung Ug1 ist nicht zulässig! Es handelt sich hierbei um eine leistungslose Steuerung, da über das
Gitter g1 fast kein Strom fließt.
1.3 Die Wirkungsweise des Schutzgitters
In einem geschlossenen Stromkreis können sich die an den einzelnen Bauelementen anliegenden Spannungen ändern. So kann sich auch die zwischen der Anode und der Kathode anliegende Spannung
während des Betriebs einer Röhre in einer Schaltung (z.B. Verstärkerschaltung) ändern. Die Änderung der Anodenspannung Ua hat ebenfalls Einfluss auf den Betriebszustand der Elektronenröhre.
Eine Änderung der Anodenspannung Ua beeinflusst das elektrische Feld in der Röhre und damit letztendlich auch den Elektronenstrom (Anodenstrom). Gewünscht ist aber eine Anodenstromsteuerung
nur durch die negative Spannung des Gitters g1. Um diese Beeinflussung des Betriebszustandes der
Röhre zu reduzieren wird gemäß Bild 1.1 ein Gitter g2 in die Röhre eingebracht. An das Schutzgitter
g2 wird eine gegenüber der Kathode positive Spannung Ug2 angelegt. Das Gitter g2 dominiert nun die
Verteilung des elektrischen Feldes zwischen Kathode und Gitter g2. Durch die konstante Spannung
Ug2 an Gitter g2 wird nun das Feld zwischen Kathode und Gitter g2 stabilisiert. Damit wird eine
Beeinflussung durch die weiter entfernte Anode reduziert. Die Elektronen zwischen der Kathode und
dem Gitter g2 werden nun hauptsächlich durch das Gitter g2 in Richtung der Anode beschleunigt.
Die Pentoden- Kennlinien auf Blatt 8 des Datenblattes [1] zeigen eine deutliche Abflachung im oberen
Spannungsbereich Ua . Bei einer reinen Änderung der Anodenspannung ändert sich der Anodenstrom
nur geringfügig. Das Schutzgitter g2 begrenzt im oberen Spannungsbereich von Ua die Raumladung,
welche zur Anode gelangen kann. Vergleichen Sie den prinzipiellen Kennlinienverlauf einer Pentode
mit der Kennlinie einer Triode.
Die auf das Gitter g2 anfliegenden Elektronen werden nur in sehr geringer (unwesentlicher) Anzahl
vom positiven Gitter g2 aufgesogen. Dies liegt zum einen an der hohen Geschwindigkeit der Elektronen, wenn sie das Gitter g2 passieren. Die meisten Elektronen schießen einfach auf Grund ihrer
Geschwindigkeit durch das Gitter g2 hindurch. Zum anderen ist das Gitter g2 so konstruiert, dass die
Elektronen nur in möglichst geringer Zahl am Gitter hängen bleiben können.
1.4 Die Wirkungsweise des Bremsgitters
Das Bremsgitter wird einfach mit der Kathode verbunden. Damit übt das Bremsgitter auf das anfliegende Elektron eigentlich eine abstoßende Kraft aus. Jedoch ist hier die Geschwindigkeit des Elektrons
so hoch, dass es das Bremsgitter g3 fast unbeeinflusst durchfliegt und in die Anode einschlägt. Der
Einschlag des Elektrons auf der Anode kann dabei so heftig sein, dass ein anderes Elektron wieder
aus der Anode herausgeschlagen wird. Dieses Elektron vagabundiert aber sehr langsam von der Anode
weg. Diese Elektronen werden vom Bremsgitter gestoppt, um dann wieder von der Anode angezogen und aufgesogen zu werden. Ohne Bremsgitter könnten die herausgeschlagenen Elektronen zum
Schirmgitter zurückfliegen. Dies würde den Anodenstrom verringern und zu Verzerrungen führen.
2 Erläuterungen zu Gleich- und Wechselstromwiderstand
Auf den Unterschied von Gleichstrom- und Wechselstromwiderstand muss man bei jeder gekrümmten
Kennlinie achten. So hat zum Beispiel auch ein Gleichrichter sowohl einen Gleichstromwiderstand als
auch einen davon abweichenden Wechselstromwiderstand. Diesen Wechselstromwiderstand nennt man
meistens den differentiellen oder dynamischen Widerstand [2]. Bild 2.1 zeigt die Zusammenhänge. Hier
sind die für die beiden Widerstände maßgeblichen Dreiecke 0AB und ACD eingetragen.
Der Gleichstromwiderstand wird durch die Steigung der Geraden durch den Nullpunkt und dem
Arbeitspunkt beschrieben. Dieser Wert entspricht dem Widerstand im aktuellen Arbeitspunkt, und
Dipl.-Ing.(FH) Thomas Peschko
2 von 5
Theorie zum Versuch nicht Lineare Bauelemente im MET-Labor
Abbildung 2.1: Bestimmung von Gleich- und Wechselstromwiderstand für den Punkt nach [2]
wird durch Gleichung (2.1) berechnet. Es ist zu beachten das dieser Widerstandswert nur in diesem
einen Arbeitspunkt gilt.
∆Ua_
tan(β) =
= Ri_ .
(2.1)
∆Ia_
Der Wechselstromwiderstand wird durch die Steigung der Tangente im Arbeitspunkte beschreiben.
Dabei handelt es sich um eine Linearisierung der Kennlinie um Berechnung zu vereinfachen. Aus Bild
2.1 ist leicht ersichtlich das diese Näherung nur für einen kleinen Bereich um den Arbeitspunkt gilt,
da ansonsten die Abweichung zur realen Kennlinie zu groß wird.
tan(α) =
∆Ua
= Ri ,
∆Ia
(2.2)
Für die Auslegung von Schaltungen mit Elektronenröhren ist der sogenannte Röhrenkennwert (auch
Innenwiderstand) wichtig, welcher wie folgt definiert ist.
Ri =
δUa
δIa
mit
Ug = konstant.
(2.3)
Dieser Wert charakterisiert den Widerstand den die Röhre an der Ausgangsseite hat. Für eine nicht
zu stark gekrümmt Kennlinie kann dieser Wert durch Gleichung (2.2) angenähert werden [2].
3 Eine einfache Röhrenverstärkerschaltung
Die Elektronenröhre EF 98 kann vereinfacht als ein stufenlos steuerbarer Widerstand dargestellt werden. Dabei wird hier zunächst angenommen, dass Ua konstant gehalten wird. Die Steuerung des Widerstandes erfolgt dann über die an das Gitter g1 angelegte Spannung Ug1 . Je negativer die Spannung
am Gitter g1 gegenüber der Kathode ist, desto höher ist der Gleichstromwiderstand der Röhre.
Dipl.-Ing.(FH) Thomas Peschko
3 von 5
Theorie zum Versuch nicht Lineare Bauelemente im MET-Labor
mit Ug2 = 3, 2 V und Ug3 = 0 V
Abbildung 3.1: Stark vereinfachte Darstellung einer Röhre als steuerbarer Widerstand
3.1 Einführende Betrachtungen
In einem ersten Schritt wollen wir die Röhre als einen mittels der Gitterspannung Ug1 steuerbaren
Widerstand (s.h. Gleichung (2.3)) betrachten. Hierzu legen wir zum Beispiel zwischen der Anode und
der Kathode eine konstante Gleichspannung von UB = 6, 3 V an. Die Anschlüsse der anderen Gitter
werden in dieser stark vereinfachten Darstellung nicht gezeigt.
Im nächsten Schritt wird nun ein rein ohmscher Widerstand Ra in Reihe geschaltet. Dadurch ergibt
sich die in Bild 3.2a dargestellte Anordnung. Es entsteht ein einfacher Spannungsteiler. Dabei ist
zu beachten, dass sich der Widerstand der Röhre durch eine Variation der angelegten Spannung ug1
ändert. Dies hat Einfluss auf die Aufteilung der Batteriespannung auf die beiden Bauelemente. Steigt
zum Beispiel die Spannung an der Röhre sinkt die Spannung am Widerstand Ra . Es gilt zu jedem
Zeitpunkt Gleichung (3.1). Folgende Illustration soll die Zusammenhänge verdeutlichen.
(a) Schaltung mit Arbeitswiderstand
(b) Wirkungsweise der Schaltung
Abbildung 3.2: Stark vereinfachte Röhre mit Arbeitswiderstand Ra
Wenn nun zum Beispiel ∆ug1 = 0, 2 V und ∆uRa = 2 V ist, dann ergibt sich eine Verstärkung mit
Faktor v = 10. Aus Bild 3.2a ergibt sich mittels des Maschensatzes:
Ra = ia + ua = UB
(3.1)
1
UB
· ua +
Ra
Ra
(3.2)
Gleichung (3.1) umgestellt nach ia :
ia = −
Dipl.-Ing.(FH) Thomas Peschko
4 von 5
Theorie zum Versuch nicht Lineare Bauelemente im MET-Labor
Gleichung (3.2) stellt eine Geradengleichung mit negativer Steigung dar. Sie schneidet die Ordinate
im positiven Bereich. Sie stellt die möglichen ua ia -Kombinationen dar, welche mit dem verwendeten Widerstand Ra und der Spannungsquelle UB möglich sind. Die Gleichung (3.2) nennt man
Arbeitsgerade. Zur Konstruktion der Arbeitsgeraden ist es hilfreich zwei theoretische Betrachtungen
durchzuführen:
1. Röhre ist vollkommen leitend. ua = 0 V, ia =
UB
Ra
→ P1 (0 V, URBa )
2. Röhre sperrt vollkommen. ua = UB , ia = 0 mA → P2 (UB , 0 mA)
Jede Kurve des Kennlinienfelds im Datenblatt [1] stellt eine Funktion im Sinne der Mathematik
dar. Die Arbeitsgerade wird durch die Funktionsgleichung (3.2) dargestellt. Die Funktion der Arbeitsgeraden und die Funktion einer Kurve stellen somit ein Gleichungssystem mit zwei Gleichungen und
den zwei Unbekannten ua und ia dar. Mathematisch kann man solche Gleichungssysteme durch besondere Verfahren lösen. Es handelt sich um eine Reihenschaltung. Der Strom in der Röhre und der
Strom durch den Widerstand Ra ist identisch. Die graphische Lösung besteht in der Suche nach dem
Schnittpunkt der beiden Funktionsgraphen. Der Schnittpunkt der Arbeitsgeraden mit einer Kurve des
Datenblattes gibt somit die sich einstellende Spannung an der Röhre ua und den sich einstellenden
Strom ia an.
Literatur
[1] Electronis, P. :
Philips Electronic Tube Handbook: Electronic tube.
HörstelRiesenbeck: AK Modul- Bus Computer GmbH (Electronic tubes Bd. 1-3).
http://www.ak-modul-bus.de/cat/documentation/EF98.pdf
[2] SCHRÖDER, H. : Elektrische Nachrichtentechnik II. Band. Verlag für Radio- Foto- Kinotechnik
GmbH, 1963
Dipl.-Ing.(FH) Thomas Peschko
5 von 5