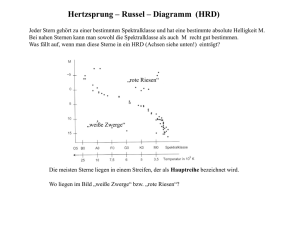
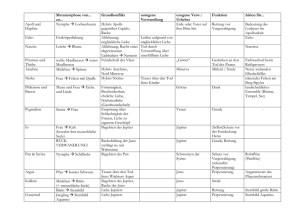
Q12 * Astrophysik * Klausur aus der Physik * 11.01

Q12 * Astrophysik * Klausur aus der Physik * 11.01.2013
1. Astronomische Koordinatensysteme
Regulus ist der Hauptstern im Sternbild Löwe mit den folgenden astronomischen
Koordinaten: Deklination 12,0o ; Rektaszension: 10,1 h
a) Bestimmen Sie mit einer geeigneten Zeichnung die obere Kulminationshöhe
von Regulus für einen Beobachter in München (geographische Breite 48o).
Begründen Sie, dass Regulus für München nicht zirkumpolar ist.
b) Welche geographische Breite müsste ein Ort auf der Nordhalbkugel der Erde
haben, dass Regulus dort zirkumpolar erscheint?
c) Kann man Regulus auch in Johannesburg (26,2o südlich, 28,1o östlich) beobachten?
Wenn ja, welche maximale Höhe über dem Horizont erreicht Regulus dort?
2. Planetensystem
Juno ist ein Asteroid aus dem Asteroiden-Hauptgürtel zwischen Mars und Jupiter.
Die Zeitspanne zwischen zwei Oppositionen beträgt 1a 109d und die Bahn von Juno
weist eine Exzentrizität von 0,255 auf.
a) Berechnen Sie die siderische Umlaufdauer Junos.
Bestimmen Sie daraus die große Halbachse von Junos Ellipsenbahn!
[Ergebnisse: Tsid = 4,35 a, aJuno = 2,66 AE ]
b) Berechnen Sie die Aphel- und Periheldistanz Junos.
c) Um wie viel Prozent vergrößert sich die Geschwindigkeit Junos bei ihrem Weg
vom Aphel zum Perihel?
3. Sonne
a) Berechnen Sie die Masse der Sonne mit dem bekannten Wert von 1 AE = 1, 496 1011 m
und weiteren geeigneten Daten.
b) Beobachtet man die Sonne durch ein feststehendes Fernrohr (mit Sonnenfilter!), so
wandert diese in 2min 8s um genau einen Sonnendurchmesser weiter.
Ermitteln Sie mit Hilfe dieser Beobachtung den Sonnenradius zu 6,96 108 m .
c) Berechnen Sie die Fallbeschleunigung an der Sonnenoberfläche in Vielfachen der
Erdbeschleunigung g .
Astronomische Daten:
m3
G  6, 67 1011
;
kg  s2
Aufgabe 1a
Punkte
5
b
3
M  1,989 1030 kg ; 1 AE  1, 496 1011 m
c
3
2a
5
b
3
c
5
3a
4
b
4
c
4
Summe
36
Gutes Gelingen! G.R.
Q12 * Astrophysik * Klausur aus der Physik * 11.01.2013 * Musterlösung
1. a) Für die obere Kulminationshöhe ho gilt
o
o
o
Zenit
N
h o  90      90  48  12  54
o
o
Beobachter zu b)
München-Beobachter
Regulus liegt bei der unteren Kulmination
h u  180o    90o    30o unterhalb
des Horizonts.
Regulus

.

ho
ho
b) Die untere Kulmination muss oberhalb
des Horizonts verlaufen, d.h. im
Grenzfall gilt
  90o    180o   90o  12o  78o
Für eine geographische Breite   78o ist
Regulus zirkumpolar.
 = 48

ÄE
ÄE Äquator-Ebene
o
 = 12,0o
Horizont-Ebene
Johannesburg
Beobachter
Johannesburg
HE
HE Horizont-Ebene
München
c) In Johannesburg kulminiert Regulus im Norden, und zwar in einer (maximalen) Höhe
von h o,Johannesburg  90o  Joh    90o  26, 2o  12,0o  51,8o .
2. a)
1
1
1
1
1




 Tsid  1589d  4,35a
Tsid TErde Tsyn 365, 25d 474, 25d
2
2
 4,35a 
 a Juno   Tsid,Juno 
3
  a Juno  1AE  
  2, 66 AE

 
 1AE   1, 00a 
 1, 00a 
3
b) rAphel  (1  )  a Juno  1, 255  2,66AE  3,34AE und
rPerihel  (1  )  a Juno  0,745  2,66AE  1,98AE
c) v Aphel 
 2
1 
G  M 

 
r
a
Juno 
 Aphel
6, 67 10
v Perihel 
11
m3
1 
1
km
 2
1,989 1030 kg  


 14,1

2
11
kg  s
s
 3,34 2, 66  1, 496 10 m
 2
1 
G  M 


 rPerihel a Juno 
6, 67 1011
m3
1 
1
km
 2
1,989 1030 kg  


 23, 7

2
11
kg  s
s
 1,98 2, 66  1, 496 10 m
vPerihel 23, 7

 1, 68 , d.h. die Geschwindigkeit erhöht sich um 68%.
vAphel 14,1
Einfacher:
v Perihel

v Aphel
 2
1 
G  M 


 rPerhel a Juno 
 2
1 
G  M 


r
 Aphel a Juno 

1 
 2
 1,98  2, 66 

  1, 686...  1, 69
1 
 2
 3,34  2, 66 


3. a) Aus dem Kraftansatz für die Bewegung der Erde um die Sonne folgt:
GmM
FZentripetal  FGravitation  m  2  r 

r2
2  r 3 4  2  r 3
4  2  (1, 496 1011 m)3
M 


 1,99 1030 kg
3
2
m
G
T G
(365, 25  24  3600s)2  6, 67 1011
kg  s 2
b) Der „Winkeldurchmesser“ der Sonne beträgt nach der Angabe
r
360o 128s


 0,5333o und
 tan 
24  3600s
1AE
2
r  1, 496 1011 m  tan
0,5333o
 6,96 108 m
2
c) An der Sonnenoberfläche gilt für eine Masse m:
GmM
FGewicht  FGravitation  m  g 

r 2
g 
GM

r 2
m3
1,989 1030 kg
2
m 2, 73,8
kg  s
 273,8... 2 
g  27,9g
8
2
(6,96 10 m)
s
9,81
6, 67 1011