Basiswissen 5. Klasse

Basiswissen 5. Klasse
1. Daten
Zur Darstellung von Daten werden oft Strichlisten, Figurendiagramme oder
Säulen- und Strichdiagramme verwendet.
Strichliste:
Alter
Strichliste
Anzahl
5-10 Jahre
|||
3
10-15 Jahre
||||
4
15-20 Jahre
|
1
Figurendiagramm:
Alter
5-10 Jahre
☺☺☺
10-15 Jahre
☺☺☺☺
15-20 Jahre
☺
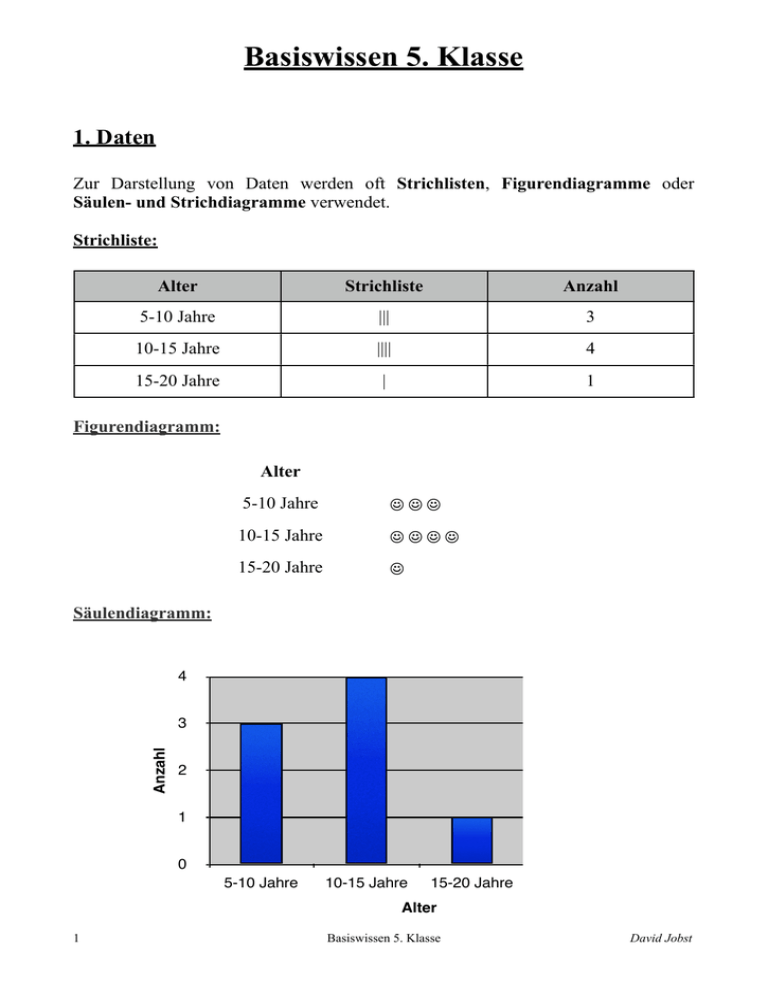
Säulendiagramm:
4
Anzahl
3
2
1
0
5-10 Jahre
10-15 Jahre
15-20 Jahre
Alter
1
Basiswissen 5. Klasse
David Jobst
Strichdiagramm:
4
Anzahl
3
2
1
0
5-10 Jahre
10-15 Jahre
15-20 Jahre
Alter
2. Große natürliche Zahlen
Zehnerpotenzen: Die Stufenzahlen des Zehnersystems lassen sich in Form von
Potenzen darstellen. Die hochgestellte Zahl nennt man Exponent. Die Zahl unter
dem Exponenten nennt man Basis. Basis und Exponent heißen zusammen Potenz.
Der Exponent gibt an, wie oft die Basis mit sich selbst multipliziert werden
muss.
Potenz
BasisExponent
Beispiel: 10 · 10 · 10 · 10 · 10 · 10 · 10 = 107 = 10 000 000
1
2
3
4
5
6
7
Stellenwerttafel: Sie dient zum leichteren Lesen von großen Zahlen.
Beispiel:
Billionen
Milliarden
Millionen
Tausender
HB ZB B
HMd ZMd Md
HM ZM M
HT ZT T
7
2
9
1
4
6
7
0
3
2
Basiswissen 5. Klasse
1
5
8
H Z E
3 9 0
David Jobst
Die Menge der natürlichen Zahlen  enthält unendlich viele Zahlen.
Menge der natürlichen Zahlen:  = {1;2; 3; 4;5;6;...}
Menge der natürlichen Zahlen einschließlich der Zahl 0:  0 = {0;1;2; 3; 4;5;6;...}
3. Summen und Differenzen
Addieren: Zusammenzählen von Zahlen nennt man Addieren. Die zugehörige
Rechenart heißt Addition.
Beispiel:
10
+
17
= 37
1. Summand
2. Summand Wert der Summe
Summe
Subtrahieren: Abziehen von Zahlen nennt man Subtrahieren. Die zugehörige
Rechenart heißt Subtraktion.
Beispiel:
17
Minuend
-
10
=7
Subtrahend Wert der Differenz
Differenz
Rundungsregel Kurzfassung: Man rundet die Zahlen so, dass man geschickt im
Kopf rechnen kann. Bei Zahlen kleiner als 5 wird abgerundet und bei Zahlen
größer als 5 wird aufgerundet.
Beispiel: 23 694 + 80 297 = ?
24 000 + 80 000 = 104 000
Schriftliches Addieren und Subtrahieren: Einer, Zehner, ... werden untereinander
geschrieben und nacheinander addiert oder subtrahiert. Man kann aber auch
nebeneinander addieren oder subtrahieren.
Beispiel:
4345
+ 244
4589
3
4345
8756 + 714161 = 9502
− 244
4101
Basiswissen 5. Klasse
David Jobst
4. Vorteilhaftes Rechnen
Assoziativgesetz der Addition: In einer Summe darf man beliebig Klammern
setzen oder weglassen, ohne dass sich der Wert der Summe ändert.
a + b + c = (a + b) + c = a + (b + c)
Beispiele: 2 + 3 + 4 = (2 + 3) + 4 = 2 + (3 + 4) = 9
12 + 9 + 11 = (12 + 9) + 11 = 12 + (9 + 11) = 32
Kommutativgesetz der Addition: In einer Summe darf man die Reihenfolge der
Summanden ändern, ohne dass sich der Wert des Summe verändert.
a+b=b+a
Beispiele: 4 + 3 = 3 + 4 = 7
11 + 9 + 21 = 21 + 11 + 9 = 41
Tipps zur Rechenreihenfolge:
1. Berechnen der Klammern
2. Sortieren der Glieder
3. Zusammenfassen
Beispiel: 67 - 12 + (7 + 1) + 43 - 3 = 55 + 8 + 40 = 95 + 8 = 103
Beachte bei Termgliederung: Die zuletzt ausgeführte Rechenart legt die Art des
Terms fest.
5. Messen unterhalb der Null
Beachte: Werte von Größen können unterhalb der Null liegen. Gekennzeichnet
sind sie durch ein vorangestelltes Minuszeichen.
Man kennt bis jetzt nur positive ganze Zahlen z.B. 1, 2, 3, ... . Die Zahlen mit dem
vorangestellten Minuszeichen nennt man negative ganze Zahlen z.B. -1, -2, -3, ... .
Die Null ist neutral und somit weder positiv noch negativ. Die positiven ganzen
Zahlen, die Null und die negativen ganzen Zahlen bilden die Menge der ganzen
Zahlen  .
Menge der ganzen Zahlen:  = {...− 4;−3;−2;−1;0;1;2; 3; 4;...}
4
Basiswissen 5. Klasse
David Jobst
Beispiele: -7°C; -500€ Schulden, ...
6. Die Zahlengerade und erste Rechnungen
Zahlengerade: Sie stellt einen Ausschnitt der Menge der ganzen Zahlen dar, d.h.
die negativen Zahlen, die Null und die positiven Zahlen. Je weiter man nach rechts
geht, desto größer werden die Zahlen. Die gewöhnliche Einheit ist 1 cm.
Gegenzahlen: Zahlen, die sich im Vorzeichen unterscheiden und gleich weit von
der Null entfernt sind, heißen Gegenzahlen.
Beispiel: -3 ist die Gegenzahl von 3. Umgekehrt ist 3 die Gegenzahl von -3.
Beide Zahlen sind 3 Einheiten von der Null entfernt.
Addition von Zahlen:
-5 + 9 = 4
Subtraktion von Zahlen:
+9
8 - 10 = -2
-10
5
Basiswissen 5. Klasse
David Jobst
7. Vereinfachung der Addition und Subtraktion ganzer Zahlen
Addition einer negativen Zahl: Man subtrahiert die Gegenzahl.
Beispiel: 20 + (-15) = 20 - 15 = 5
Subtraktion einer negativen Zahl: Man addiert die Gegenzahl.
Beispiel: 20 - (-15) = 20 + 15 = 35
Beachte: Rechen- und Vorzeichen müssen durch Klammern getrennt werden.
Beispiel: 22 + (-11) - (-3) = 22 - 11 + 3 = 11 + 3 = 14
8. Das Koordinatensystem
Koordinatensystem: Es besteht aus einer x-Achse, die waagrecht verläuft, und
einer y-Achse, die senkrecht verläuft. Beide Achsen teilen die Zeichenebene in
vier Quadranten (I, II, III, IV) ein, die gegen den Uhrzeigersinn angeordnet sind.
Jeder Punkt P kann in das Koordinatensystem mit P (x/y) eingetragen werden.
Dabei geht man von Null (= Ursprung des Koordinatensystems) aus um x auf der xAchse nach rechts oder links und dann von dort aus um y nach oben oder unten.
Beispiel:
Punkt A (1/3)
Um 1 auf der x-Achse nach rechts von Null (= Ursprung des Koordinatensystems)
aus und von dort um 3 in y-Richtung nach oben.
Punkt B (-1/-2)
Um 1 auf der x-Achse nach links von Null (= Ursprung des Koordinatensystems) aus
und von dort um 2 in y-Richtung nach unten.
6
Basiswissen 5. Klasse
David Jobst
9. Geometrische Grundbegriffe und Figuren
Strecke: Geradlinige Verbindung zweier Punkte.
Beispiel: Strecke a oder [AB]
Halbgerade: Besitzt einen Anfangspunkt,
aber keinen Endpunkt.
Beispiel: Halbgerade h oder [AB
Gerade: Besitzt weder Anfangspunkt noch
Endpunkt.
Beispiel: Gerade g oder AB
Parallele Geraden: Geraden, die zueinander
parallel sind, haben überall denselben
Abstand d.
Beispiel: Gerade g1 und g2
Schreibweise: g1⎟⎟ g2
Senkrechte (orthogonale) Geraden: Geraden, die
zueinander senkrecht sind, schließen einen rechten
Winkel miteinander ein.
Beispiel: Gerade g1 und g2
Schreibweise: g1 ⊥ g2
Diagonale im Rechteck: Verbindungsstrecke
zwischen zwei gegenüberliegenden Eckpunkten.
Beispiel: [BD] und [AC]
Radius r: Die Verbindungsstrecke von Mittelpunkt zu
einem Punkt auf der Kreislinie. Hier: z.B. r = [MA]
Durchmesser d: Die Verbindungsstrecke zweier Punkte
auf der Kreislinie, die auch den Mittelpunkt enthält. Hier:
z.B. d = [AB]
Für die Längen der Strecken gilt hier:
r = MC = MA = MB und AB = 2 ⋅ MA
7
Basiswissen 5. Klasse
David Jobst
10. Winkel
Beachte: Winkel werden immer gegen den Uhrzeigersinn gedreht.
Schreibweise:
α = ASB
β = BSA
A: Punkt auf dem 1. Schenkel
S: Scheitel
B: Punkt auf dem 2. Schenkel
Nullwinkel: α = 0°
Spitzer Winkel: 0° < β < 90°
Rechter Winkel: γ = 90°
Stumpfer Winkel: 90° < δ < 180°
Gestreckter Winkel: ε = 180°
Überstumpfer Winkel: 180° < η < 360°
Vollwinkel: ϕ = 360°
8
Basiswissen 5. Klasse
David Jobst
11. Achsensymmetrische Figuren
Achsensymmetrie: Eine Figur ist dann achsensymmetrisch, wenn man die Figur so
falten kann, dass beide Hälften genau deckungsgleich aufeinander zu liegen
kommen.
Symmetrieachse: Die Faltgerade ist die Symmetrieachse.
Bildpunkt: Jeder Punkt einer Figur wird von der einen Seite der Symmetrieachse
im gleichen Abstand auf die andere Seite auf gleicher Höhe gespiegelt. Diesen
Punkt nennt man Bildpunkt.
Beispiel: Die Punkte C und C‘ sind Bildpunkte, weil ihre Verbindungsstrecke von der
Achse senkrecht halbiert wird. Dasselbe gilt für A und A‘ bzw. B und B‘.
12. Zerlegen in Faktoren
Multiplizieren: Malnehmen von Zahlen nennt man Multiplizieren. Die zugehörige
Rechenart heißt Multiplikation.
Beispiel:
10
1. Faktor
·
17
= 170
2. Faktor Wert des Produkts
Produkt
Kommutativgesetz der Multiplikation: In einem Produkt darf man die
Reihenfolge der Faktoren ändern, ohne dass sich der Wert des Produkts verändert.
a·b=b·a
Beispiele: 4 · 3 = 3 · 4 = 12
11 · 9 · 21 = 21 · 11 · 9 = 2079
9
Basiswissen 5. Klasse
David Jobst
Assoziativgesetz der Multiplikation: In einem Produkt darf man beliebig
Klammern setzen oder weglassen, ohne dass sich der Wert des Produkts ändert.
a · b · c = (a · b) · c = a · (b · c)
Beispiele: 2 · 3 · 4 = (2 · 3) · 4 = 2 · (3 · 4) = 24
9 · 12 · 33 = (9 · 12) · 33 = 9 · (12 · 33) = 3564
Primzahlen: Das sind Zahlen, die genau zwei Teiler haben, nämlich 1 und sich
selbst.
Beispiele: 2, 3, 5, 7, 11, 13, 15, ...
Primfaktorzerlegung: Zerlegung einer natürlichen Zahl in ein Produkt, dessen
Faktoren nur Primzahlen sind. Bei mehrfachem Auftauchen einer Primzahl
verwendet man die Potzenschreibweise.
Beispiel: 432 = 16 · 27 = 8 · 2 · 9 · 3 = 2 · 2 · 2 · 2 · 3 · 3 · 3
Potenzschreibweise:
Beispiel:
Potenz
BasisExponent
2·2·2·2=24
1
2
3
4
Beispiel: 432 = 16 · 27 = 8 · 2 · 9 · 3 = 2 · 2 · 2 · 2 · 3 · 3 · 3 = 24 · 33
Quadratzahlen: Potenzen mit dem Exponenten 2.
Dividieren: Teilen von Zahlen nennt man Dividieren. Die zugehörige Rechenart
heißt Division.
Beispiel:
20
Dividend
:
10
Divisor
=7
Wert des Quotienten
Quotient
Beachte: Die Division durch 0 ist nicht erlaubt!
Beispiel: 23 : 0 = „NICHT ERLAUBT!“
0 : 23 = 0 „ERLAUBT!“
10
Basiswissen 5. Klasse
David Jobst
13. Rechnen mit natürlichen Zahlen
Distributivgesetz für Summen: Bei einem Produkt aus einer Zahl und einer
Summe darf man jeden Summanden mit der Zahl multiplizieren und im
Anschluss, falls möglich, die entstehenden Produkte addieren. Der Wert des Terms
ändert sich dabei nicht.
a · (b + c) = (b + c) · a = a·b + a·c
Beispiele: 3 · (4 + 2) = 3 · 4 + 3 · 2 = 12 + 6 = 18
43 · 6 = (40 + 3) · 6 = 40 · 6 + 3 · 6 = 258
Distributivgesetz für Differenzen: Bei einem Produkt aus einer Zahl und einer
Differenz darf man den Minuenden und den Subtrahenden mit der Zahl
multiplizieren und im Anschluss, falls möglich, die entstehenden Produkte
subtrahieren. Der Wert des Terms ändert sich dabei nicht.
a · (b - c) = (b - c) · a = a·b - a·c
Beispiele: 2 · (7 - 3) = 2 · 7 - 2 · 3 = 14 - 6 = 8
29 · 7 = (30 - 1) · 7 = 30 · 7 - 1 · 7 = 203
Tipps für die Rechenreihenfolge:
Klammern vor
Potenzen vor
Punkt vor
Strich!
14. Schriftliche Multiplikation und Division
Schriftliche Multiplikation: Jede Ziffer des zweiten Faktors wird mit dem ersten
Faktor multipliziert und dann jeweils darunter geschrieben. Anschließend erfolgt
eine ganz normale Addition. (Stellen beachten!)
2154 · 345
6462
8616
+ 10770
743130
11
Basiswissen 5. Klasse
David Jobst
Schriftliche Division: Ein geeigneter Teil des Dividenden wird durch den Divisor
dividiert, der jeweilige verbleibende Rest durch die nachfolgenden Ziffern des
Dividenden ergänzt.
26425 : 25 = 1057
- 25↓↓
142
- 125↓
175
- 175
0
・26 : 25 = 1 → 1 Rest 1 → 1 ist die erste Zifffer des
Ergebnisses
・nächste Ziffer des Dividenden (4) von oben „holen“
14 : 25 = ?; 25 geht 0 mal in 14 → 0 ist die zweite
Ziffer des Ergebnisses
・weitere Ziffer (2) von oben „holen“
142 : 25 = 5 Rest 17 → 5 ist die dritte Ziffer des
Ergebnisses
・letzte Ziffer des Dividenden (5) von oben „holen“
175 : 25 = 7 Rest 0 → 7 letzte Ziffer des Ergebnisses
→ die Division geht auf
15. Das Zählprinzip
Baumdiagramme: Zur Veranschaulichung mehrerer Kombinations- und
Wahlmöglichkeiten.
Zählprinzip: Die Gesamtanzahl an Wahlmöglichkeiten entspricht der Anzahl
der Baumenden.
Beachte: Man muss sich darüber im Klaren sein, ob sich das Zählprinzip auf eine
Stufe oder mehrere Stufen bezieht.
Beispiel: Aus drei Körben mit Bällen
wird jeweils ein Ball gezogen. Im
ersten Korb liegen zwei Bälle, einer
mit der Aufschrift 1, einer mit der
Aufschrift 2. Ebenso im zweiten
Korb. Im dritten Korb liegen 3 Bälle
mit den Aufschriften 1, 2 und 3. Wie
viele verschiedene Zahlen können
gebildet werden, wenn der erste Korb
die Hunderter - ,der zweite Korb die
Zehner - ,der dritte Korb die
Einerstelle der Zahl liefert?
Lösung: 2 · 2 · 3 = 12 Möglichkeiten
12
Basiswissen 5. Klasse
David Jobst
16. Multiplikation ganzer Zahlen
Tipp: Man multipliziert zuerst die ganzen Zahlen, ohne dass man auf die Vorzeichen
achtet. Im Anschluss legt man die Vorzeichen fest.
Vorzeichenregeln:
(+) · (+) = +
(+) · (-) = (-) · (+) = (-) · (-) = +
Beispiele: 2 · 4 = 8
3 · (-5) = -15
(-2) · 6 = -12
(-4) · (-9) = 36
3 ·0=0
0 · (-2) = 0
17. Division ganzer Zahlen
Tipp: Man dividiert zuerst die ganzen Zahlen, ohne dass man auf die Vorzeichen
achtet. Im Anschluss legt man die Vorzeichen fest.
Vorzeichenregeln:
(+) : (+) = +
(+) : (-) = (-) : (+) = (-) : (-) = +
Beispiele: 8 : 4 = 2
6 : (-2) = -3
(-18) : 3 = -6
(-25) : (-5) = 5
(-3) : 0 = „NICHT ERLAUBT!“
0 : 2 = 0 „ERLAUBT“
13
Basiswissen 5. Klasse
David Jobst
18. Größen im Alltag
Beispiele für Größen: 4 kg, 12 €, 90 cm, 23 s, Maßzahl Einheit, ...
Umrechnungsfaktor
1.Größe ←⎯⎯⎯⎯⎯
→ 2.Größe...
100
Euro ←⎯
⎯
→ Cent
1000
10
10
10
km ←⎯⎯
→ m ←⎯
→ dm ←⎯
→ cm ←⎯
→ mm
1000
1000
1000
t ←⎯⎯
→ kg ←⎯⎯
→ g ←⎯⎯
→ mg
24
60
60
Tag ←⎯
→ h ←⎯
→ min ←⎯
→s
Umwandeln in eine kleinere Einheit: Multiplikation der Maßzahl mit dem
Umrechnungsfaktor und Verwenden der kleinen Einheit.
Beispiel: 45 km = 45 · 1000 m = 45 000 m
Umwandeln in eine größere Einheit: Division der Maßzahl durch den
Umrechnungsfaktor und Verwenden der größeren Einheit.
Beispiel: 32 000 kg = 32 · 1000 kg = 32 · 1 t = 32 t
oder (32 000 kg : 1000) t = 32 t
19. Größen in Kommaschreibweise
Tipp: Das Komma wird um so viele Stellen verrutscht, wie der
Umrechnungsfaktor Nullen besitzt. Um Größen vergleichen zu können, braucht
man die gleiche Einheit.
Umwandeln in die größere Einheit: Komma nach links
Umwandeln in die kleinere Einheit: Komma nach rechts
Beispiel: 2345 m in km:
2345 m = 2,345 km
(3 Stellen ≙ 3 Nullen beim Umrechnungsfaktor 1000)
12,54 m = 1254 cm
20. Addition und Subtraktion von Größen
Tipp: Größenangaben mit gleichen Einheiten lassen sich ganz normal addieren und
subtrahieren. Die Kommas müssen jedoch genau untereinander stehen. Bei
verschiedener Stellenzahl können nach dem Komma Nullen ergänzt werden für eine
bessere Übersicht.
Beispiel:
857,45 €
857,45 €
45,30 €
45,30 €
+ 1,18 €
- 1,18 €
903,93 €
810,97 €
14
Basiswissen 5. Klasse
David Jobst
21. Multiplikation und Division von Größen
Bei der Multiplikation multipliziert man die Größe mit der Zahl zuerst ohne
Beachtung des Kommas. Nach der Multiplikation setzt man so das Komma, dass
das Ergebnis genauso viel Nachkommastellen wie die Maßzahl hat.
Bei Multiplikationen mit 10, 100, 1000, 10000, ... rutscht man das Komma um die
Anzahl der Nullen nach rechts.
Beispiele:
32,56 € · 3 = 97,68 €
23,235 m · 100 = 2323,5 m
Dividiert man eine Größe durch:
- eine natürliche Zahl, so ergibt sich wieder eine Größe
- eine andere Größe (derselben Einheit), so ergibt sich eine Zahl ohne Einheit.
Beim Dividieren setzt man das Komma, wenn das Komma beim Dividenden
erreicht ist. Reichen die Ziffern zum Dividieren nicht aus, dürfen nach dem
Komma Nullen ergänzt werden. Bei Division durch 10, 100, 1000, 10000, ... rutscht
man das Komma um die Anzahl der Nullen nach links.
Beispiel:
18,30 kg : 3 = 6,10 kg
-18
03
- 3
00
- 00
0
22. Maßstab und Umfang
Maßstab: Gibt an, wie Längen der Wirklichkeit auf einem Plan dargestellt sind.
z.B. 1 : 500 bedeutet, dass die Längen in Wirklichkeit 500 mal so lang sind wie im
Plan. 500 ist die „Maßstabszahl“.
wahre Länge = (1 : Maßstabszahl) · Länge im Plan
Länge im Plan = wahre Länge : (1 : Maßstabszahl)
Maßstabszahl = wahre Länge : Länge im Plan
15
Basiswissen 5. Klasse
David Jobst
Beispiel:
a) Maßstab 1:4000, Länge im Plan 5 cm
→ wahre Länge = 4000 · 5 cm = 20 000 cm = 200 m
b) Maßstab: 1:4000, Länge in der Wirklichkeit 500 m
→ Länge im Plan = 500 m : 4000 = 500 000 mm : 4000 = 125 mm = 12,5 cm
c) Länge im Plan 5 cm, Känge in der Wirklichkeit 25 m
→ Maßstabszahl = 2500 cm : 5 cm = 500 → 1 : 500 Maßstab
Umfang: Summe aller Seitenlängen von Figuren.
Umfang eines Rechtecks:
u=l+b+l+b= l+l+b+b
u=2·l+2·b
Umfang eines Quadrats:
u=a+a+a+a
u=4·a
23. Flächeninhalt
Definition Flächeninhalt: Die Größe einer Fläche wird als Flächeninhalt
bezeichnet. Man kann ihn z.B. durch Auslegen der Fläche mit kleineren
Flächenstücken (z.B. Kästchen) messen.
16
Basiswissen 5. Klasse
David Jobst
24. Flächeneinheiten
Flächeninhalte können in unterschiedlichen Flächeneinheiten angegeben werden.
Die Flächeneinheiten ergeben sich aus den Inhalten von „Einheitsquadraten“:
Seitenlänge des Quadrats
Flächeninhalt
1 mm
1 mm2
1 cm
1 cm2
...
...
→ Der Umrechnungsfaktor zwischen „benachbarten Einheiten“ beträgt immer 100.
Umrechnungsfaktor
1.Größe ←⎯⎯⎯⎯⎯
→ 2.Größe...
100
100
100
100
100
100
km 2 ←⎯
⎯
→ ha ←⎯
⎯
→ a ←⎯
⎯
→ m 2 ←⎯
⎯
→ dm 2 ←⎯
⎯
→ cm 2 ←⎯
⎯
→ mm 2
Beispiel: 384 ha = 38 400 a
472 cm2 = 4,72 dm2
25. Flächenformeln
Flächeninhalt Rechteck:
ARechteck = Länge · Breite
ARechteck = l · b
Beispiel: Länge = 8 cm; Breite = 4 cm
ARechteck = l · b = 8 cm · 4 cm = 32 cm2
Flächeninhalt Quadrat:
AQuadrat = Seitenlänge · Seitenlänge
AQuadrat = a · a
AQuadrat = a2
Beispiel: Seitenlänge = 8 m
AQuadrat = 8 m · 8 m = 64 m2
17
Basiswissen 5. Klasse
David Jobst
Flächeninhalt rechtwinkliges Dreieck:
Der Flächeninhalt eines rechtwinkligen Dreiecks entspricht der Hälfte eines
Rechtecks, da man das Rechteck in zwei gleich große rechtwinklige Dreiecke
zerlegen kann.
ADreieck = (Länge · Breite) : 2
ADreieck = l · b : 2
Beispiel: Länge = 8 cm; Breite = 4 cm
ADreieck = l · b : 2= 8 cm · 4 cm : 2 = 16 cm2
Flächeninhalt Parallelogramm:
Die Fläche eines Parallelogramms lässt sich so zerlegen, dass wieder ein Rechteck
entsteht.
AParallelogramm = Länge · Höhe
AParallelogramm = l · h
Beispiel: Länge = 8 m; Höhe = 4 m
ARechteck = l · h = 8 m · 4 m = 32 m2
26. Der Oberflächeninhalt eines Quaders und eines Würfels
Quader:
Man stelle sich den Quader wie ein
Zimmer vor. Der Quader besitzt am
Boden und an der Decke zwei gleich
große Rechtecke
(A1 = 2 · Länge · Breite). Zudem besitzt
der Quader an der Vorderseite und an
der Rückseite zwei gleich große
Rechtecke (2 · Länge · Höhe = A2).
Außerdem sind die beiden Flächen, die
nach rechts und links gewandt sind,
gleich groß (2 · Breite · Höhe = A3).
Addiert man alle Flächeninhalte so
erhält man den Oberflächeninhalt des Quaders.
18
Basiswissen 5. Klasse
David Jobst
OQuader = 2 · Länge · Breite + 2 · Länge · Höhe + 2 · Breite · Höhe
OQuader = 2 · l · b + 2 · l · h + 2 · b · h
OQuader = 2 · (l · b + l · h + b · h)
Beispiel: Länge = 8 cm; Breite = 4 cm; Höhe = 3 cm
OQuader = 2 · (l · b + l · h + b · h)
OQuader = 2 · (8 cm · 4 cm + 8 cm · 3 cm + 4 cm · 3 cm)
OQuader = 136 cm2
Würfel:
Der Würfel besitzt sechs gleich große Flächen. Da jede Seitenlänge a lang ist,
ergibt sich für eine Fläche:
A = a · a = a2. Für den Oberflächeninhalt des Würfels muss A also mit 6
multipliziert werden.
OWürfel = 6 · Seitenlänge · Seitenlänge
OWürfel = 6 · a · a
OWürfel = 6 · a2
Beispiel: Seitenlänge = 4 m
OWürfel = 6 · a2
OWürfel = 6 · (4 m)2
OWürfel = 84 m2
Beachte: Bei Körpern, die aus Quadern und Würfeln zusammengesetzt sind, muss
man aufpassen, dass Berührflächen nicht zur Oberfläche des Körpers dazuzählen.
Beispiel:
OKörper = OQuader + OWürfel - 2 · ABerührfläche
19
Basiswissen 5. Klasse
David Jobst