1. Achsen- und Punktsymmetrie
Werbung
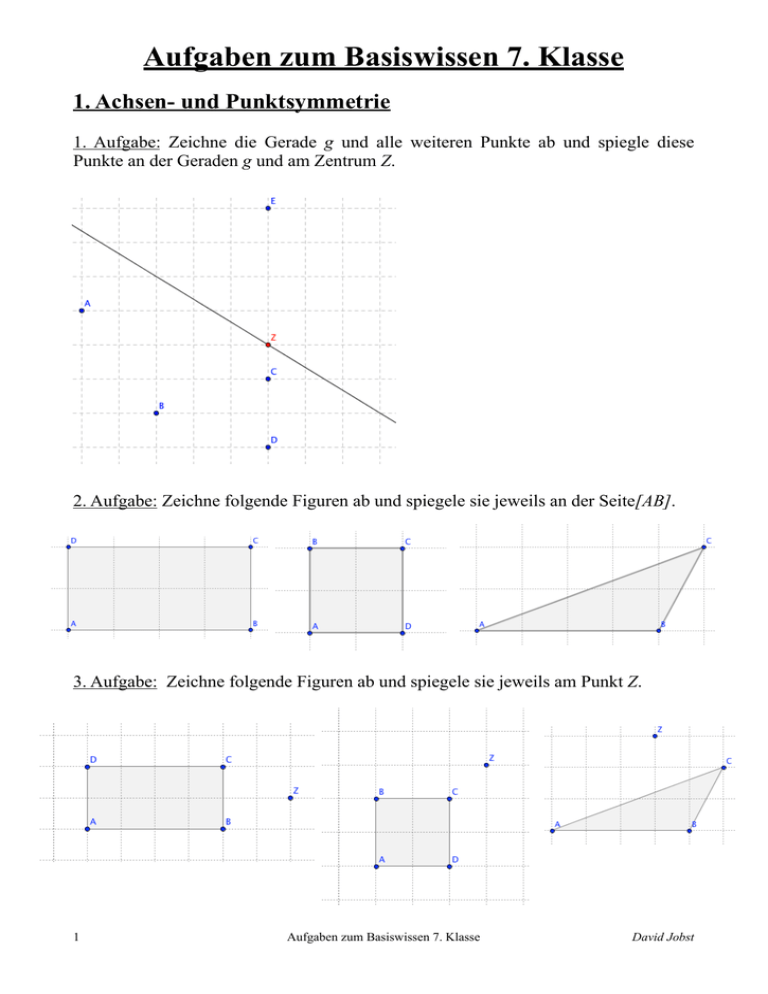
Aufgaben zum Basiswissen 7. Klasse 1. Achsen- und Punktsymmetrie 1. Aufgabe: Zeichne die Gerade g und alle weiteren Punkte ab und spiegle diese Punkte an der Geraden g und am Zentrum Z. 2. Aufgabe: Zeichne folgende Figuren ab und spiegele sie jeweils an der Seite[AB]. 3. Aufgabe: Zeichne folgende Figuren ab und spiegele sie jeweils am Punkt Z. 1 Aufgaben zum Basiswissen 7. Klasse David Jobst 2. Symmetrische Vierecke 1. Aufgabe: Zeichne jeweils ein symmetrisches Viereck ABCD mit folgenden Eigenschaften: a) Die jeweils gegenüberliegenden Seiten sind parallel und gleich lang. Alle Winkel betragen 90°. Die Längen der Seiten betragen 4 cm und 2 cm. b) Die gegenüberliegenden Seiten [AB] und [CD] sind parallel, aber unterschiedlich lang. [AB] ist 5 cm und [CD] 3 cm lang. c) Die benachbarten Winkel ergänzen sich jeweils zu 180° und gegenüberliegende Seiten sind parallel zueinander. Die gegenüberliegenden Seiten sind jeweils gleich lang, wobei AB = 6 cm ist und BC = 3 cm ist. 2. Aufgabe: Nenne jeweils die Eigenschaften von Raute, gleichschenkligem Trapez und Drachenviereck. 3. Aufgabe: Überprüfe folgende Behauptungen. a) Jedes Rechteck hat so viele Symmetrieachsen, wie es Seiten hat. b) Jedes Trapez hat zwei Paar parallele Seiten. c) Jedes Parallelogramm hat zwei Paar parallele Seiten. 3. Grundkonstruktionen 1. Aufgabe: Überprüfe, ob die roten Linien tatsächlich die Winkelhalbierenden des jeweiligen Winkels sind. 2 Aufgaben zum Basiswissen 7. Klasse David Jobst 2. Aufgabe: a) Zeichne die Punkte A (-2/1), B (2/1) und C (-3/5) in ein Koordinatensystem ein und verbinde anschließend die Punkte zum Dreieck ABC. b) Konstruiere alle möglichen Mittelsenkrechten und zeige, dass sie sich in einem Punkt M schneiden. c) Konstruiere den Umkreis, d.h. den Kreis um M durch die Eckpunkte des Dreiecks. 3. Aufgabe: a) Zeichne die Punkte A (-2/1), B (4/-1), C (3/2) und D (-3/4) in ein Koordinatensystem ein. Welches besonderes Viereck ist ABCD? b) Errichte die Mittelsenkrechten zu [AB] und [CD]. c) Konstruiere die Winkelhalbierende für ∢ CBA. 4. Entdeckungen an Geraden- und Doppelkreuzungen 1. Aufgabe: Berechne die Größe des Winkels α mit Begründung. 2. Aufgabe: Berechne die Größe des Winkels α mit Begründung. 3 Aufgaben zum Basiswissen 7. Klasse David Jobst 5. Entdeckungen an Dreiecken und Vierecken 1. Aufgabe: Berechne die fehlende Winkelmaße mit Hilfe der Eigenschaften von Dreiecken. 2. Aufgabe: Berechne die fehlenden Winkel in den Dreiecken mit Begründung. 4 Aufgaben zum Basiswissen 7. Klasse David Jobst 3. Aufgabe: Berechne die fehlenden Winkel mit Begründung. 6. Terme aufstellen und Termwerte berechnen 1. Aufgabe: Übertrage die Tabelle in dein Heft und berechne die entsprechenden Termwerte. a -3 0 0,5 4 T (a) = a2 + 2a -1 T (a) = 3,5a - 6 T (a) = a3 -3a -1 2. Aufgabe: Übertrage die Tabelle in dein Heft und berechne die entsprechenden Termwerte. a -3 0 0,5 4 b -2 0,5 2 3 T (a; b) = 3ab2 + 2b - a T (a; b) = a - b + 4 T (a; b) = a3b-3ab2 -7 5 Aufgaben zum Basiswissen 7. Klasse David Jobst 3. Aufgabe: Übertrage die Tabelle in dein Heft und finde jeweils passende Terme. a -1 0 2,5 6 -3 -2 0,5 3,5 2 1 7,25 37 2 4 9 16 7. Abhängigkeiten beschreiben und untersuchen 1. Aufgabe: Untersuche, welche Zahl jeweils nicht für die Variable eingesetzt werden darf. 1 3 T2 (a) = T3 (a) = 12a − 7 a−4 5a − 3 2. Aufgabe: Bei welchem Term steigt der Termwert am schnellsten? T1 (a) = T1 (a) = 5a + 3 T2 (a) = a 2 − 3 T3 (a) = 24a 3 − a 3. Aufgabe: Bei welchem Term sinkt der Termwert am schnellsten? T1 (a) = 4 4+a T2 (a) = 1 a2 T3 (a) = 3 2a − 5 8. Daten und Diagramme 1. Aufgabe: Die Tabelle zeigt die Besucherzahlen des Zoos. Berechne die durchschnittliche Besucherzahl pro Monat. Jan 440 Feb 540 März April 490 600 Mai 640 Juni 900 Juli 980 Aug 720 Sep 630 Okt 590 Nov 460 Dez 470 2. Aufgabe: Stelle die Werte aus der Tabelle in Aufgabe 1 graphisch mit einem Säulendiagramm dar. 6 Aufgaben zum Basiswissen 7. Klasse David Jobst 3. Aufgabe: Erstelle zu folgender Grafik eine Wertetabelle. Mitgliederzahlen im Fußballverein Mitgliederzahlen 200 150 100 50 0 Januar März Mai Juli September November 9. Wiederholen und Vertiefen des Prozentrechnens 1. Aufgabe: Übertrage die Tabelle in dein Heft und fülle die Lücken. a) Grundwert Prozentsatz 35 € 10 % b) c) 15 % 800 € Prozentwert 12 € 160 € 2. Aufgabe: a) Der Computer kostet zu Beginn 599 €. Berechne wie viel er kostet, nachdem der Preis auf 80 % des ursprünglichen Preises herabgesetzt wird. b) Ein Fahrrad kostet anfangs 400 €. Aufgrund des Räumungsverkaufs wird es um 17 % reduziert. Um wie viel Euro ist es günstiger? 3. Aufgabe: Eine Schulklasse geht ins Kino und bestellt 25 Karten à 7 € vor. Jedoch bekommt die Klasse jede Karte 15 % günstiger. Wie viel Geld muss der Lehrer einsammeln? 4. Aufgabe: a) Eine BMW-Aktie verteuert sich um 5 % auf 2625 €. Berechne den ursprünglichen Preis. b) Eine Apple-Aktie verliert um 10 % an Wert und kostet nur noch 207 €. Berechne den ursprünglichen Preis. 7 Aufgaben zum Basiswissen 7. Klasse David Jobst 10. Zusammenfassung der Rechengesetze für rationale Zahlen 1. Aufgabe: Fasse soweit wie möglich zusammen. a) b) c) d) e) f) 4x + (3y + 6x) -3a + (5b - 9a) 8c - (-2x - 7b) 4y - (-y + 4x) -3 + (5,2a + 8,3) -(-z - 0,9) - 2,8 2. Aufgabe: Fasse soweit wie möglich zusammen. a) b) c) d) e) f) 13a - (2b - 5a) - [(14b - 7a) + 15b] -(8y + 5x) - (2y - 13x + 8x - y) -24 + (-23p + 17) + [-(q - 15p) + 19q] -7x - [4y - (26y - x) + (3x + 5y)] -[-12uv + (7uv - uv) - (u +17v)] -18abc - [-35bc + (-13abc + 46bc)] 3. Aufgabe: Multipliziere aus. a) b) c) d) e) f) 7 · (3n + 4a) (-3) · (-8 + 2x) 6n · (3 - 9) 5 · (-3ae + 4bi) 11 · (5d + 3ef - 4fe) 0,25 · (12x - 12y + 36) 4. Aufgabe: Vereinfache soweit wie möglich. a) b) c) d) e) f) 8· (-6a - b) + 6 · (-6b + 6a) 5· (9c - 4d) - (45c + 23d) · 2 (5c - 8d)· [4 · (3n - 3n)] [x · (3n + 4m) - (4n - 4m)· 3] - 3xn (7n - 3p)· 4 - [(-2)· (3n - 7p)] zb - bz + (-3)· (-4zb + 2zb) - zb 5. Aufgabe: Berechne mit Hilfe des Distributivgesetzes. a) 2 : 0,5 - 8 : 0,5 b) 5: 0,25 + 4 : 0,25 c) 2,5 · 4 - 8 · 2,5 d) 9,4 · 2 - 1· 9,4 + 3 · 9,4 e) 8 · 9 + 3 · 9 + 12 · 3 · 3 8 Aufgaben zum Basiswissen 7. Klasse David Jobst 11. Umformen von Summen und Produkten 1. Aufgabe: Fasse soweit wie möglich zusammen. a) 6x 4 y 2 z 3 ⋅ 5x 2 y 2 z b) 12d 2 c ⋅ 2d 2 c 2 e c) 4a 2 d 2 ⋅ 5da 3 ⋅(-6cd 5 ) d) -3,6r 2 s 3t 4 ⋅(0,5rst)2 e) -0,5cp ⋅ dp ⋅(6dp 2 )3 f ) 2,5a ⋅ 6b 2 ⋅(-3)a 2b 3 2. Aufgabe: Fasse soweit wie möglich zusammen. a) 12rs 2 − 32r 3s + 50rs 2 + 5r 3s b) 3a 3c 3 − 34a 4 c 5 + 32a 3c 3 − 22a 4 c 5 + 2ad c) 7e 2 f 4 g 3 − (-3e 3 f 3g 4 + 12e2 f 4 g 3 − 14e3 f 3g 4 ) d) 45j7 k 6l 3 − (15 j 2 k 3l 4 + 15 j 7 k 6l 3 − 25 j 2 k 3l 4 ) − 20 j 7 k 6l 3 e) 20m 2 n 5 r − 20m 2 r 5 n 2 + 32r 2 mn − (23r 2 mn + 3r 5 m 2 n 2 ) f ) 73o 3 p 4 a 2 − (31o 3 p 4 a 3 + 29o 3 p 4 a − o 3 p 4 a 3 ) − (12o 3 p 4 a + o 3 p 4 a 3 ) 12. Klammerregeln - Das Multiplizieren von Summen und Differenzen 1. Aufgabe: Berechne. a) b) c) d) e) f) (a + 1) · (2a + 3) (2b - 3)· (3b - 2) (3 + 7,2a)· (0,5b - 2) (2,8x2 + 22)· (x3 + 1) (3,5x3 - 4)· (x + y) (x2 + 3x - 3)· (2 - x) + 6 2. Aufgabe: Vereinfache soweit wie möglich. a) b) c) d) e) 9 (x - 2)· (x + 1) + 1,5x2 + 2 (-y + 6)· (y - 0,25) - (-3 + y2) -2x· (0,5x + y - 0,25) + 2y· (-0,2x - 0,75y) 4· (0,5x - 2)· (4x + 3) - (x - 3)· (x - 7) -(a - b + 1)· (a + b) + a· (a + b) Aufgaben zum Basiswissen 7. Klasse David Jobst 13. Durch Probieren und Überlegen zur Lösung 1. Aufgabe: Löse im Kopf. a) 3x + 3 = 15 b) 12x - 3 = 21 c) 8x + 9 = 73 d) 4y + 2 = 22 e) 28k + 1 = 57 f) 44x + 22 = 66 2. Aufgabe: Finde die Lösung durch geschicktes Einsetzen. a) 4x + 12 = 28 b) -45x - 32 +12 = -155 c) x2 = 188 - 44 3. Aufgabe: Überprüfe, ob die Lösungen richtig sind und verbessere sie gegebenfalls. a) 5x + 15 = 65 b) -10x - 66 + 46 = -155 c) x2 = 312 - 56 d) x3 = 64 x=4 x = 13,5 x1 = 16 und x2 = -16 x=6 14. Lösung einer Gleichung 1. Aufgabe: Bestimme die Lösungsmenge mit Hilfe von Äquivalenzumformungen. a) b) c) d) e) f) 3x + 4 = 16 7x + 23 = 58 8x - 3 = 61 3 + 10x = 123 12x - 3 = 93 5x + 8 = 45 2. Aufgabe: Bestimme die Lösungsmenge. a) 8x - 15 = 2x - 3 b) 3x + 27 = 4x + 3 c) (-2)· (4 - 7x) + 2x = -4 d) 5 + 2· (x - 15) = 8 e) 5· (5 - 6x) = 16 - 3x 3. Aufgabe: Bestimme die Lösungsmenge. a) 4x + 4 · (3 - 5x) - 10 = 5 - 15x b) -13x + 2· (0,5x + 1) - (22 + x) = 6 10 Aufgaben zum Basiswissen 7. Klasse David Jobst c) -8x + 5x - 3· (3x + 4x) = 4· (-8 + 2x) + 8x d) (-2)· (2,5x + 1) + 3x - 2 = 3x - 1 15. Kongruente Figuren 1. Aufgabe: Was bedeutet kongruent? 2. Aufgabe: Zeichne zwei zueinander kongruente Dreiecke. 3. Aufgabe: Zeichne zwei zueinander kongruente gleichschenklige Trapeze. 16. Kongruenzsätze für Dreiecke 1. Aufgabe: Was besagen die einzelnen Kongruenzsätze genau? Erkläre anhand von Skizzen. 2. Aufgabe: Überprüfe durch geeignete Sätze, ob die Dreiecke ABC konstruierbar sind. a) a = 2 cm; b = 3,6 cm; c = 3 cm b) ∢ACB = 120 °; a = 5 cm; b = 2 cm c) ∢ACB = 150 °; ∢ABC = 90 °; c = 6 cm 3. Aufgabe: Konstruiere jeweils ein geeignetes Dreieck ABC und ergänze dann die Lücken. a) a b 5 cm 5,5 cm b) c) c ∢CBA ∢ACB 75° 4,6 cm 3,5 cm ∢BAC 118° 4,1 cm 44° 96° 17. Besondere Dreiecke 1. Aufgabe: Konstruiere jeweils mit der vorgegebenen Seitenlänge ein gleichseitiges Dreieck. Gib zusätzlich jeweils die Größe der Winkel an a) a = 6 cm b) a = 34 mm 11 Aufgaben zum Basiswissen 7. Klasse David Jobst 2. Aufgabe: Konstruiere mit den angegebenen Stücken jeweils ein gleichschenkliges Dreieck. a) a = b = 4,9 cm; ∢ACB = 49° b) a = c = 0,5 dm; ∢CBA = 72° c) a = c = 3 cm; ∢BAC = 66° 3. Aufgabe: Konstruiere ein rechtwinkliges Dreieck ABC (∢ACB = 90°) mit der Höhe hc = 3 cm, wobei AB = c = 8 cm . 18. Besondere Linien und Punkte im Dreieck und Konstruktion 1. Aufgabe: Zeichne ein Dreieck ABC mit A (-2/1), B (2/1) und C (-3/5). Konstruiere anschließend den Umkreis. 2. Aufgabe: Konstruiere ein Dreieck ABC mit den Längen a = 3 cm; b = 7 cm; c = 5 cm. Konstruiere die Winkelhalbierenden der Innenwinkel. 3. Aufgabe: Konstruiere ein Dreieck mit den Längen a = 4 cm; b = 5 cm; c = 6 cm. Konstruiere jeweils in der Mitte der Strecken [AB], [BC] und [AC] Lote. Welche besondere Bedeutung hat der Schnittpunkt dieser Lote? 12 Aufgaben zum Basiswissen 7. Klasse David Jobst