Repetition Geometrie / Vektoren
Werbung

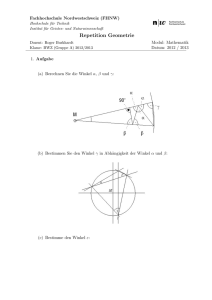
Fachhochschule Nordwestschweiz (FHNW) Hochschule für Technik Institut für Geistes- und Naturwissenschaft Repetition Geometrie / Vektoren Dozent: Roger Burkhardt Klasse: BWZ 2013/2014 Büro: 5.1C05 Semester: - Modul: Mathematik Datum: 2013 / 2014 1. Aufgabe (a) Berechnen Sie die Winkel α, β und γ: (b) Bestimmen Sie den Winkel γ in Abhängigkeit der Winkel α und β: (c) Bestimme den Winkel ε: Mathematik Repetition Geometrie / Vektoren 2013 / 2014 2. Aufgabe (a) Bestimmen Sie die Grösse x (g und h sind parallele Geraden): (b) In einem Zimmer mit Dachschräge sollen drei Regalbretter in den Höhen h1 = 0.9m, h2 = 1.2m und h3 = 1.5m angebracht werden. Auf welche Längen l1 , l2 und l3 müssen die Regalbretter zugeschnitten werden? Seite 2 / 7 Mathematik Repetition Geometrie / Vektoren 2013 / 2014 3. Aufgabe (a) Bestimmen Sie die Länge der gemeinsamen Tangente (x) in Abhängigkeit der Kreisradien (R1 , R2 ) und der Distanz zwischen den Kreismittelpunkten (d): (b) Bestimmen Sie den Radius des kleinen Kreises in Abhängigkeit der Seitenlänge des Quadrates: Seite 3 / 7 Mathematik Repetition Geometrie / Vektoren 2013 / 2014 4. Aufgabe Berechnen Sie bei den folgenden rechtwinkeligen Dreiecken die fehlenden Seiten und Winkel: (a) c = 110, 6m, α = 35.6◦ (b) a = 40mm, β = 20◦ (c) a = 84m, h = 35m 5. Aufgabe (a) Das untere Ende einer 10m langen Leiter, die gegen eine senkrechte Wand gelehnt ist, ist von der Wand 2m entfernt. Welchen Winkel schliesst die Leiter mit dem waagrechten Boden ein und wie hoch ist das obere Ende der Leiter über dem Boden? (b) Ein Skifahrer fährt in einen unter 50◦ geneigten Hang ein. i. Berechnen Sie die Steigung des Hanges. Seite 4 / 7 Mathematik Repetition Geometrie / Vektoren 2013 / 2014 ii. Wie viele Meter längs der Falllinie legt der Skifahrer zurück, wenn er einen Höhenunterschied von 250m überwindet? iii. Welche horizontale Entfernung legt der Skifahrer zurück, wenn er einen Höhenunterschied von 250m überwindet? (c) Ein senkrecht aufsteigender Ballon wird von einem Punkt P der 1500m vom Aufstiegsort des Ballons entfernt ist, unter dem Höhenwinkel α = 32◦ gesehen. Zwei Minuten später erscheint er unter dem Höhenwinkel β = 38◦ . Der Punkt P und der Aufstiegsort haben dieselbe Meereshöhe. i. Wie viele Meter ist der Ballon in der Zwischenzeit gestiegen? ii. Mit welcher Geschwindigkeit (in km/h) steigt der Ballon? iii. Wie hoch steht der Ballon nach weiteren 5min, wenn er mit derselben Steiggeschwindigkeit weiter steigt? 6. Aufgabe Gegeben sind die Vektoren −2 −3 1 → − → − −c = 0 a = 3 , b = 2 und → 6 3 7 (a) Berechnen Sie die folgende Linearkombination: → → − − − −c d = 3→ a + 2 b − 4→ (b) Bestimmen Sie die folgenden Beträge: • − |5→ a | =? • → − → a − 2 b =? 3− (c) Berechnen Sie: • • → − → → − − a ◦ 2 b − c =? → → − → − → − − b − c × b + c =? 7. Aufgabe Gegeben sei die folgende Anordnung: Seite 5 / 7 Mathematik Repetition Geometrie / Vektoren 2013 / 2014 (a) Bestimmen Sie die Koordinaten der Punkte A, B und C. −→ −→ (b) Bestimmen Sie die Vektoren AB und AC. (c) Bestimmen Sie die Fläche des schraffierten Dreiecks. (d) Bestimmen Sie die Koordinatengleichung der Ebene durch die drei Punkte A, B und C. 8. Aufgabe → − → → − − (a) Was kann man aus der Gleichung a + b + c = 0 schliessen? → − → − → → − − (b) Unter welchen Voraussetzungen für die Vektoren a und b gilt a + b = → − − |→ a | + b ? (c) Der Schwerpunkt S eines Dreiecks mit den Eckpunkten A, B und C lässt sich nach folgender Formel Berechnen: 1 → − − → → − rA + r→ rS = (− B + rC ) 3 Lösen Sie die Gleichung nach − r→ C auf. (d) Wie lauten die Koordinaten des Punktes M , welcher in der Mitte zwischen A (1, 3, −2) und B (7, 1, 4) liegt? 9. Aufgabe Durch die beiden Geraden g1 (durch den Punkt P1 (4, 0) mit der Steigung m = 13 ) und g2 (durch die Punkte P2 (0, 3) und P3 (3, 1)) wird aus dem ersten Quadranten ein Viereck ausgeschnitten. (a) Bestimmen Sie die Geradengleichungen. (b) Bestimmen Sie die Eckpunkte des Vierecks. (c) Bestimmen Sie die Seitenlängen, Innenwinkel und die Fläche des Vierecks. Seite 6 / 7 Mathematik Repetition Geometrie / Vektoren 2013 / 2014 10. Aufgabe Im Dreieck ABC mit A (8, −5, −1), B (−1, 11, 3) und C (2, −3, 9) sind die drei Höhenvektoren und die Längen der drei Höhen zu bestimmen. 11. Aufgabe Gegeben sei die Gerade durch die Punkte P (1, 3, −5) und Q (3, −2, 1). (a) Bestimmen Sie die Geradengleichung. (b) Welcher Punkt C1 auf der Geraden ergibt mit den Punkten A1 (2, 2, 5) und B1 (1, 5, −3) ein gleichschenkliges Dreieck mit A1 B1 als Basis? (c) Welcher Punkt D auf der Geraden liegt dem Ursprung am nächsten? (d) Welcher Punkt C2 auf der Geraden ergibt mit den Punkten A2 (2, 2, −2) und B2 (3, 1, −2) ein rechtwinkliges Dreieck mit A2 B2 als Hypotenuse? Seite 7 / 7