Werbung

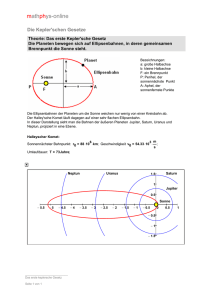
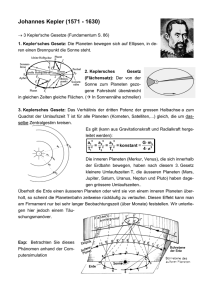
DIE 3 KEPLER’SCHEN GESETZE DER PLANETENBEWEGUNGEN 1. GESETZ Kepler erkannte, dass die Planetenumlaufbahnen keine Kreise waren (so wie es damals auch von den reformierten Wissenschaftlern angenommen wurde) sonder Ellipsen sind die sich jedoch nicht allzu sehr von der Form eines Kreises unterscheiden. 2. GESETZ In seinem 2. Gesetz ging er genauer auf die Geschwindigkeit der Planetenbewegung ein. Er formulierte das folgendermaßen: Die Verbindungslinie Sonne-Planet überstreicht in gleichen Zeiten gleiche Flächen. Aber wieso ist das so? Nun, Kepler konnte dieses Phänomen nur beschreiben. Mit der newton’schen Gravitationstheorie die erst nach seinem Tod von Newton entdeckt wurde können wir es aber auch erklären: Wie schon erwähnt bewegen sich die Planeten auf konstanten elliptischen Umlaufbahnen. Damit ein Planet aber in seiner Umlaufbahn bleiben kann, muss die Summe der Kräfte die ihn zur Sonne hinziehen und deren die ihn wegziehen gleich groß sein. Das heißt es muss eine entgegengesetzte Kraft zur Anziehungskraft der Sonne existieren. Diese Kraft ist die Fliehkraft, die bei allen Objekten auftritt, die ihre Richtung ändern, und auf einer elliptischen Umlaufbahn wird die Bewegungsrichtung ja dauernd geändert). Wenn man diese Erkenntnis als Gleichung ausdrückt lautet diese wie folgt: FGravitation = FFliehkraft Wenn jetzt der Planet der Sonne nähre kommt, was bei einer elliptischen Umlaufbahn unvermeidbar ist, wirkt die Anziehungskraft stärker auf den Planeten als zuvor, und laut der vorhin aufgestellten Formel muss deswegen die Fliehkraft auch größer werden, damit der Planet nicht in die Sonne stürzt. Dies geschieht dadurch, dass er schneller wird, denn größer Radialbeschleunigung bedeutet gleichzeitig auch eine größere Fliehkraft als vorher. Deshalb ist ein Planet in Sonnennähe schneller als in Sonnenferne. 3. GESETZ In seinem letzten Gesetz fand Kepler einen Weg die Umlaufbahnen zweier Planeten miteinander zu vergleiche. Dazu braucht man die Informationen über die Umdrehungsdauer und den größten Abstand zu der Sonne (große Halbachse „a“ einer Ellipse) eines Planeten und eine dieser beiden Variablen vom anderen Planeten. Und schon kann man sich die fehlende Variable des zweiten Planeten ausrechnen. Dieses 3. Gesetz können wir uns bekannten Formeln herleiten (was Kepler nicht möglich war Æsiehe Newton’sches Gravitationsgesetz). Dazu nehmen wir zunächst die schon vorhin aufgestellte Gleichung her... Legende: F = Kraft G = Gravitationskonstante M = Masse der Sonne (in diesem Fall) m = Masse des Planeten (in diesem Fall) a = große Halbachse einer Ellipse r = Radius eines Kreises a Beschleunigung = Beschleunigung ω = Winkelgeschwindigkeit t = Zeit ... und wir setzen darin ein ... auf der linken Seite die newton’sche Gravitationsformel, wobei wir r durch a welche die große Halbachse einer Ellipse ist ersetzen: auf der rechten Seite die Berechnung der Fliehkraft, die man aus der Formel (ebenfalls von Newton) F = m * a Beschleunigung , weil die Beschleunigung im Falle der Fliehkraft die Radialbeschleunigung ist setzen wir ra = r * ω 2 ein ,ersetzen auch hier „r“ durch a und setzen in die obige Formel ein: gleichgesetzt sieht das dann so aus m können wir auf beiden Seiten kürzen und anstatt von ω 2 *π ein: setzen wir den Berechnungsweg dieser Variable t nun bringen wir alle Konstanten Parameter auf eine Seite der Gleichung, und erhalten eine Formel mit der man sogar Planeten verschiedener Sonnensysteme vergleichen könnte... ...da Kepler diese Formel nur für unser Sonnensystem gedacht hatte, können wir M zu den konstanten Parameter zählen, und wir haben Keplers 3. Gesetz selbst hergeleitet! Denn Keplers 3. Gesetz lautet: t2 = KONSTANT a3 FGravitation = FFliehkraft FGravitation = G * M *m a2 FFliehkraft = m * a * ω 2 G* M *m = m * a *ω 2 2 a M 2 *π G * 2 = a * a t 2 M * t 2 4 *π = = KONSTANT G a3 t2 4 *π = = KONSTANT 3 G*M a zum Schluss möchte ich noch dieses Gesetz anhand eines Beispieles demonstrieren. Vergleichen wir hierzu die Erde mit dem Neptun: t Erde = 1 Erdenjahre (logischerweise) t Neptun = 164,6 Erdenjahre a Erde = 149,6 Mio km a Neptun ist gefragt t2 da 3 = KONSTANT können wir die a Gleichung beider Planeten gleichsetzen: t Erde 2 a Erde 3 = t Neptun 2 a Neptun 3 nun können wir einsetzen ... 12 164,6 2 = 149,6 3 a Neptun 3 und nach a Neptung auflösen, schon haben wir das Ergebnis: a Neptun = 4493,65Mio km Damit wäre mein Vortrag zu Ende und ich hoffe ich habe euch die kepler’schen Gesetze ein bisschen näher bringen können.