Grundwissen 7

Grundwissen Mathematik
7. Klasse
1/6
Grundwissen 7. Klasse
Algebra
1.Terme mit Variablen
a) Allgemeines
Treten in einem Term (Rechenausdruck) verschiedene Variablen auf, dann dürfen diese
mit verschiedenen oder mit gleichen Zahlen belegt werden.
Tritt aber dieselbe Variable mehrmals in einem Term auf, so muss sie jeweils mit derselben Zahl belegt werden.
Die Zahlen, die für eine Variable eingesetzt werden sollen, bilden die Grundmenge G.
Durch das Einsetzen von Zahlen aus G lässt sich der jeweilige Termwert berechnen.
Bsp.:
T(x) = x²- 2x + 1; G = {0; 0,5; -3}
T(0) = 0² - 20 + 1 = 1;
T(0,5) = 0,5² - 20,5 + 1 = 0,25;
T(-3) = (-3)² - 2(-3) + 1 = 16;
Abkürzende Schreibweise: 2x = 2x; xy = xy; 20(x - y) = 20(x – y);
(x – y)(x + y) = (x –y)(x + y);
b) Termumformungen
 Zwei Terme mit Variablen heißen äquivalent, wenn sie beide bei jeder möglichen
Einsetzung für die Variablen jeweils gleiche Werte annehmen.
Durch Umformungen nach den gültigen Rechengesetzen (Kommutativ- und
Assoziativgesetze, Klammerregeln) erhält man wieder äquivalente Terme.
 Summen werden vereinfacht, indem man gleichartige Summanden zusammenfasst.
Bsp.: x – y²+ 2x + y² = x + 2x – y² + y² = 3x;
3abc – 5ab – 7abc – 7ab + abc = 3abc – 7 abc + abc – 5ab – 7ab = -3abc
Grundwissen Mathematik
7. Klasse
2/6
 Zwei Summen werden multipliziert, indem man jeden Summanden der ersten Klammer
mit allen Summanden der zweiten Klammer multipliziert (unter Berücksichtigung der
Vorzeichen) und die Produkte dann addiert.
(a + b)(c + d) = ac + ad +bc + bd
Bsp.: (2x + 3y)(3 + 4x) = 6x + 8x² + 9y + 12xy;
(2x + 3y)(3 - 4x) = 6x - 8x² + 9y - 12xy;
(2x - 3y)(3 + 4x) = 6x + 8x² - 9y - 12xy;
(2x - 3y)(3 - 4x) = 6x - 8x² - 9y + 12xy;
Spezielle Produkte lassen sich schneller berechnen durch
 Die binomischen Formeln:
(a + b)²
= a² + 2ab + b²
(a – b)²
= a² - 2ab + b²
(a + b)(a – b) = a² - b²
(x² + 7)² = x4 + 14x² + 49;
(1 – 2x)² = 1 – 4x + 4x²;
(3x + 4y)(3x – 4y) = 9x² - 16y²;
(- 4x + 5y)² = 16x² - 40xy + 25 y²;
(- 3x – 5y)² = 9x² + 30xy + 25y²;
 Durch das Ausklammern eines Faktors wird aus einer Summe (Differenz) ein Produkt.
Bsp.:
-4a + 4 b = -4(a – b);
2abx – 6aby +4abz= 2ab(x – 3y + 2z);
8x – 3y = 8(x – 0,375y);
Bsp.:
2. Lineare Gleichungen
Die Lösungsmenge einer Gleichung ändert sich nicht, wenn man
 auf beiden Seiten dieselbe Zahl oder denselben Term addiert oder subtrahiert oder
 beide Seiten mit derselben von Null verschiedenen Zahl multipliziert oder dividiert.
Diese Umformungen heißen Äquivalenzumformungen. Sie führen zu äquivalenten
Gleichungen.
Bsp.:
5 – 0,5x = 3 + 0,75x;
 + 0,5x
5
= 3 + 1,25x;
-3
2
= 1,25x;
 : 1,25
1,6
= x;
= {1,6}
falls =
= {}
falls =
Eine lineare Gleichung hat entweder genau eine Zahl oder keine Zahl (unerfüllbare
Gleichung) oder alle Zahlen der Grundmenge (allgemeingültige Gleichung) als Lösung.
Bsp.:
5 – 2x = 2(2,5 – x);
=
5 – 2x = 5 – 2x;
 -5  + 2x
0 = 0;
= =
3. Prozentrechnung
Begriffe: Grundwert, Prozentsatz, Prozentwert (siehe hierzu Jahrgangsstufe 6)
 Wachstumsfaktor: Wird der Grundwert um p % erhöht, so steigt er auf das
p 
p 


1 
 -fache des ursprünglichen Wertes. 1 
 heißt Wachstumsfaktor.
 100 
 100 
Bsp.: Der Preis wird um 9 % erhöht. Der neue Preis beträgt das 1,09-fache des alten.
 Abnahmefaktor: Wird der Grundwert um p % erniedrigt, so nimmt er auf das
p 
p 


1 
 -fache des ursprünglichen Wertes ab. 1 
 heißt Abnahmefaktor.
 100 
 100 
Bsp.: Bei einer Preiserniedrigung um 12% sinkt der Preis auf das 0,88-fache des alten.
Grundwissen Mathematik
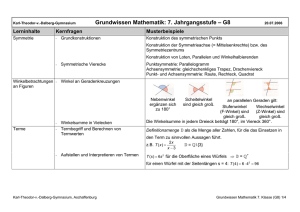
3. Symmetrische Vierecke
diagonalsymmetrisch
Drachenviereck
Raute
4/6
7. Klasse
punktsymmetrisch
mittensymmetrisch
Parallelogramm
gleichschenkliges Trapez
Quadrat
Rechteck
4. Kongruenz
Figuren, die sich beim Aufeinanderlegen decken, heißen deckungsgleich oder kongruent.
Sind zwei Figuren F und G kongruent, so schreibt man kurz:
Grundwissen Mathematik
6/6
7. Klasse
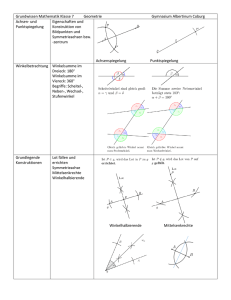
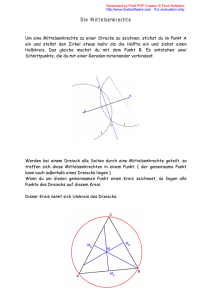
Mittelsenkrechte
b) Mittelsenkrechte zu [AB]
Kreis um A und B mit Radius r.
Die Gerade durch die Schnittpunkte ist
die Mittelsenkrechte.
A
B
c) Tangenten in einem Punkt B eines Kreises
Die Tangente steht auf dem Berührpunktsradius
senkrecht
d) Tangenten von einem Punkt P außerhalb
Der Thaleskreis über der Strecke [PM]
schneidet den Kreis k(M; r) in den
Berührpunkten B1 und B2.