Kapitel 2ab Aussagen am rechtwinkligen Dreieck -

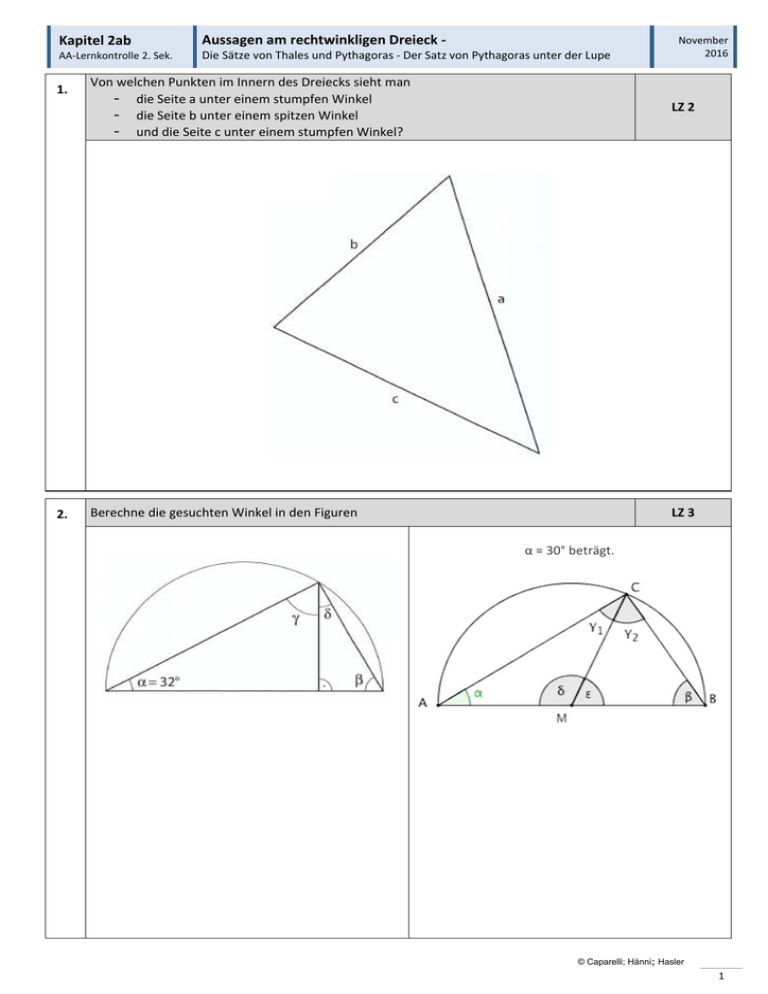
Kapitel 2ab Aussagen am rechtwinkligen Dreieck ‐ AA‐Lernkontrolle 2. Sek. Die Sätze von Thales und Pythagoras ‐ Der Satz von Pythagoras unter der Lupe 1. Von welchen Punkten im Innern des Dreiecks sieht man - die Seite a unter einem stumpfen Winkel - die Seite b unter einem spitzen Winkel - und die Seite c unter einem stumpfen Winkel? November 2016
LZ 2 2. Berechne die gesuchten Winkel in den Figuren LZ 3 α = 30° beträgt. © Caparelli; Hänni; Hasler
1 Kapitel 2ab Aussagen am rechtwinkligen Dreieck ‐ AA‐Lernkontrolle 2. Sek. Die Sätze von Thales und Pythagoras ‐ Der Satz von Pythagoras unter der Lupe November 2016
3. Berechne alle fehlenden Grössen: a = ? b = ? c = 169 m p = 25 m q = ? h = 60 m A = ? LZ 4/5 4. Berechne die fehlenden Grössen LZ 6/7 a) Grundfigur: Quadrat Seite a Diagonale d Umfang U Flächeninhalt A 24 cm 13.5 dm b) Grundfigur: Gleichseitiges Dreieck Seite a Höhe h Umfang U Flächeninhalt A 5.5 cm 22.4 mm © Caparelli; Hänni; Hasler
2 Kapitel 2ab Aussagen am rechtwinkligen Dreieck ‐ AA‐Lernkontrolle 2. Sek. Die Sätze von Thales und Pythagoras ‐ Der Satz von Pythagoras unter der Lupe November 2016
5. Wende den Satz des Pythagoras an. a.
LZ 8 Berechne den Umfang des Parallellenvierecks ABCD. b. Berechne den Umfang des Dreiecks ABC. c.
Berechne die Längen der beiden Diagonalen des Rhombus d. Berechne die Strecke x. e. Die Vierecke ABCD und EFGH sind Quadrate. Berechne die Fläche A. © Caparelli; Hänni; Hasler
3 Kapitel 2ab Aussagen am rechtwinkligen Dreieck ‐ AA‐Lernkontrolle 2. Sek. Die Sätze von Thales und Pythagoras ‐ Der Satz von Pythagoras unter der Lupe November 2016
6. Pythagoras‐Berechnungen im Koordinatensystem a.
LZ 9 Berechen den Umfang des Dreiecks b. Welches Dreieck hat den grössten Umfang, welches den kleinsten? Schätze. Berechne nun die Umfänge der Dreiecke mit Hilfe des Koordinatensystems. 7. Berechne die fehlenden Grössen: LZ 7/8 © Caparelli; Hänni; Hasler
4