Lernzielhilfen - HS
Werbung

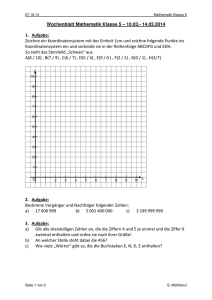
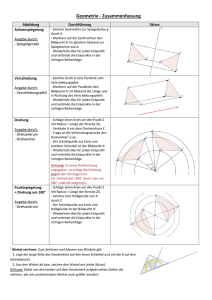
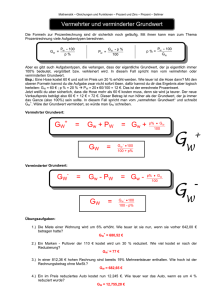
Vorbereitung auf die 6. Schularbeit aus MATHEMATIK 17.06.2011 NAME:____________________________ KL.: M2/I. - S.1 Dreieckskonstruktionen in beliebigen Viereckskonstruktionen anwenden. Ein Parallelogramm aus 2 Dreiecken Parallelogramm: a, b, α 1) Zeichne eine Skizze! 2) 3) 4) a D Zeichne die Grundlinie AB = a ! Trage beim Eckpunkt A den Winkel α auf! C f b α Trage auf dem Winkelschenkel von A aus die A Länge b auf - man erhält den Eckpunkt D! BD bildet die 3. Seite des Dreiecks ABD. b B a 5) Zeichne von D aus einen Kreisbogen mit dem Radius a und von B einen Kreisbogen mit dem Radius b - der Schnittpunkt ist der Eckpunkt C! Das 2. Dreieck mit den Seiten BC, CD und BD bildet mit dem 1. Dreieck das Parallelogramm. 6) Beschrifte das Parallelogramm! Deltoide und Trapeze konstruieren. Trapez: a, α, c, d. 1) Zeichne eine Skizze! 2) Zeichne die Grundlinie 3) 4) 5) 6) 7) AB = a D Trage beim Eckpunkt A den Winkel α auf! Trage auf dem Winkelschenkel von A aus die Länge d auf - man erhält den Eckpunkt D! Konstruiere durch D eine Parallele zu AB! Trage von D aus die Länge c auf der Parallelen auf man erhält den Eckpunkt C Verbinde BC und CD und beschrifte das Trapez! d c C b f α A B a Die Diagonalen e, f stehen nicht normal aufeinander. Nur 2 gegenüberliegende Seiten sind parallel! Deltoid: e, a, α 1) Zeichne eine Skizze! 2) Zeichne die Diagonale AC = e 3) Trage beim Eckpunkt A je einen halben Winkel α nach beiden Seiten der Diagonale e auf! 4) Markiere auf den Winkelschenkeln von A aus die Längen a = d. Man erhält den Eckpunkt B bzw. D! 5) Die Diagonale f wird als Strecke BD gezeichnet. 6) D d A α a c e f C b B Die Strecken DC und BC vervollständigen das Deltoid. Fehlende Beschriftung ergänzen! Die Diagonalen e und f stehen aufeinander normal; e teilt f genau in der Mitte. Die Winkel α und γ werden von e halbiert. Die Winkel β und δ sind gleich groß. Konstruktion von regelmäßigen Vielecken, z. B.: Sechseck, Achteck, Zwölfeck, ... 706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL Vorbereitung auf die 6. Schularbeit aus MATHEMATIK 17.06.2011 NAME:____________________________ KL.: M2/I. - S.2 Regelmäßiges Sechseck: Gegeben ist die Seite a 1) 2) 3) Konstruiere einen Kreis mit dem Radius a! 1. Möglichkeit: Schlage den Radius a sechsmal hintereinander auf der Kreislinie ab! a a M 2. Möglichkeit: Zeichne den Durchmesser ein! Schlage von seinen Endpunkten aus den Radius nach beiden Seiten auf die Kreislinie ab! Verbinde die erhaltenen Schnittpunkte zu einem Sechseck! M Regelmäßiges Zwölfeck: 1) 2) 3) 1. Möglichkeit: Zeichne ein regelmäßiges Sechseck. Die Seite a ist eine Sehne im Umkreis (mit dem Radius a)! Teile jede Sehne mit Hilfe der Streckensymmetrale. Markiere den Schnittpunkt der Symmetrieachse mit der Kreislinie! Verbinde fortlaufend je einen neuen Punkt auf der Kreislinie mit einem Eckpunkt des 6-Ecks und du erhältst ein regelmäßiges Zwölfeck! 2. Möglichkeit: Mit einer Normalen auf jeden Durchmesser des Sechsecks findest du ebenfalls die fehlenden Eckpunkte des Zwölfecks. Regelmäßiges Achteck: Zeichne ein Quadrat mit seinem Umkreis und finde die fehlenden Eckpunkte entweder durch die Seitensymmetralen oder durch Normale auf die Seiten, die gleichzeitig Durchmesser des Umkreises sind! Aus Textaufgaben mit Angabe des Grundwertes und Prozentsatzes den Prozentwert berechnen. Begriffe: Grundwert G ......... das Ganze (1 oder 100 100 oder 100 %) 1 100 vom Ganzen =$ 1 % Prozentanteil A ..... ein Teil des Ganzen in kg, Stück, ... Prozentsatz p ....... ein Teil des Ganzen in Prozentschreibweise Prozentanteil(Prozentwert)= A= Grundwert⋅Prozentsatz 100 G ⋅p 100 Aus Textaufgaben mit Angabe des Prozentsatzes und -wertes den Grundwert berechnen. 706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL Vorbereitung auf die 6. Schularbeit aus MATHEMATIK 17.06.2011 NAME:____________________________ KL.: M2/I. Begriffe: Grundwert G ......... das Ganze (1 oder 1 100 100 100 - S.3 oder 100 %) vom Ganzen =$ 1 % Prozentanteil A ..... ein Teil des Ganzen in kg, Stück, ... Prozentsatz p ....... ein Teil des Ganzen in Prozentschreibweise Grundwert = G= Prozentanteil100 ⋅ Prozentsatz A ⋅100 p Prozentsätze in Streifen- oder Kreisbildern darstellen bzw. die Prozentsätze angeben. 706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL Vorbereitung auf die 6. Schularbeit aus MATHEMATIK 17.06.2011 NAME:____________________________ KL.: M2/I. Begriffe: Grundwert G ......... das Ganze (1 oder 100 100 - S.4 oder 100 %) vom Ganzen =$ 1 % Prozentanteil A ..... ein Teil des Ganzen in kg, Stück, ... Prozentsatz p ....... ein Teil des Ganzen in Prozentschreibweise 1 100 Prozentsatz = p= Prozentanteil100 ⋅ Grundwert A⋅100 G Bsp. Der Grundbesitz eines Landwirtes besteht aus 38 % Feldern, 41 % Wiesen und 12 % Wald. Der Rest ergibt sich aus sonstigen Flächen (Gebäude, Gewässer, Straßen und Wege,..). Stelle die Daten grafisch dar! z.B. Prozentstreifen (l = 10 cm) z.B. Prozentkreis (r = 2,5 cm) 100 % =$ 10 cm 1 % =$ 0,1 cm 38 % =$ 3,8 cm (Felder) 41 % =$ 41 , cm (Wiesen) 100 % =$ 360° 1 % =$ 3,6° 38 % =$ 137° (Felder) 41 % =$ 148° (Wiesen) 12 % =$ 43° (Wald) 9 % =$ 32° (sonstigeFl.) 12 % =$ 1,2 cm (Wald) 9 % =$ 0,9 cm (sonstigeFl.) Felder Wiesen Wälder sonstige Fl. 38 % 41 % 38 % 41 % 12 % 9 % 9% 12 % Aus Textaufgaben mit Angabe des Grund- und Prozentwertes den Prozentsatz berechnen. 706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL Vorbereitung auf die 6. Schularbeit aus MATHEMATIK 17.06.2011 NAME:____________________________ KL.: M2/I. Begriffe: Grundwert G ......... das Ganze (1 oder 1 100 100 100 - S.5 oder 100 %) vom Ganzen =$ 1 % Prozentanteil A ..... ein Teil des Ganzen in kg, Stück, ... Prozentsatz p ....... ein Teil des Ganzen in Prozentschreibweise Prozentsatz = p= Prozentanteil100 ⋅ Grundwert A⋅100 G Grundrechnungsarten mit Brüchen und Dezimalzahlen durchführen. Wandle die Brüche in Dezimalzahlen oder die Dezimalzahlen in Brüche um! Beachte falls notwendig auch die Vorrangregeln! z.B.: 2 1 4 oder 2 ⋅ 0,5 = 2,25 ⋅ 0,5 = 1,125 1 4 ⋅ 1 2 = 9⋅1 4⋅2 = 9 8 = 1 1 8 Ergibt die Umwandlung eines Bruches eine periodische Dezimalzahl, so ist es besser, mit Brüchen zu rechnen! 706082 Hauptschule Vorderes Stanzertal, St. Margarethen 6551 Pians; Köck Leonhard, HL