PHYSIK I: Mechanik und Thermodynamik - Physik Uni

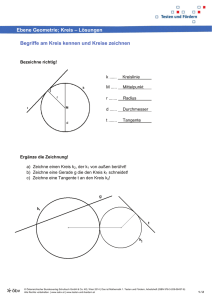
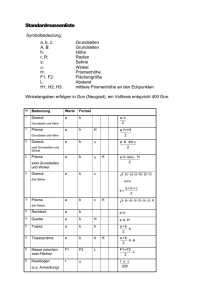
PHYSIK I: Mechanik und Thermodynamik
Übungsblatt 4
Aufgabe 1:
Die Massen in folgender Anordnung betragen m1=1,2 kg, m2=1,8 kg und m3=3,5 kg. Die Massen der
Verbindungsseile können vernachlässigt werden. Die Rollen und Räder seien reibungsfrei gelagert. Die
Anordnung wird aus dem Ruhezustand losgelassen.
a) Wie groß ist die Beschleunigung a?
b) Wie groß ist die Spannung im Seil zwischen der hängenden Masse 3 und dem Wagen?
c) Wie groß ist die Geschwindigkeit aller Massen, nachdem die Anordnung losgelassen wurde und sich
über eine Strecke von 25 cm bewegt hat?
Aufgabe 2:
Der Haftreibungskoeffizient zwischen den Reifen eines Autos und einer horizontalen Straße beträgt
µHR = 0,6. Die Gesamtkraft, die auf das Auto wirkt, sei die von der Straße ausgeübte Haftreibungskraft.
a) Wie groß ist die maximal mögliche Beschleunigung, wenn das Auto bremst?
b) Wie groß ist der Bremsweg des Autos mindestens, wenn es zunächst mit 30 𝑚⁄𝑠 fährt?
Aufgabe 3:
Bei einer Attraktion in einem Freizeitpark stehen die Fahrgäste mit dem Rücken zur Wand in einer Trommel,
die sich dreht. Plötzlich wird der Boden abgesenkt, wobei die Reibung aber verhindert, dass die Fahrgäste
hinabfallen. Der Zylinder hat einen Radius von 4m. Mit wie vielen Umdrehungen pro Minute muss sich der
Zylinder drehen, wenn der Haftreibungskoeffizient zwischen Fahrgast und Wand 0,4 beträgt?
Ausgabe am 10.11.2010, Besprechung in der Woche vom 15.-19.11.2010
Seite 1
PHYSIK I: Mechanik und Thermodynamik
Übungsblatt 4
Aufgabe 4:
Nennen Sie Beispiele für eine Bewegung, bei der Geschwindigkeits- und Beschleunigungsvektoren
a) in die entgegengesetzte Richtung zeigen.
b) in die gleiche Richtung zeigen
c) senkrecht aufeinander stehen.
Aufgabe 5:
In der Vorlesung wurde für die Coriolisbeschleunigung bzw. –kraft folgende Formeln angegeben:
 

a c = −2ω × v

 
Fc = 2mv × ω
Machen Sie sich nochmals anhand folgenden Gedankenexperiments das Zustandekommen der Formel klar:
Ein Ball rollt vom Punkt M mit einer Geschwindigkeit v in Richtung der x-Achse eines Inertialsystems S.
Gleichzeitig rotiert ein System S‘ um Punkt M. Beim Losrollen seinen die x- und x‘-Achse identisch.
Bestimmen Sie nun welchen Kreisbogen s die Kugel im System S‘ scheinbar zurückgelegt hat (also den
Kreisbogen zwischen x- und x‘-Achse in Abhängigkeit vom Radius r). Verwenden Sie nun für den
Kreisbogen die aus der Newtonschen Mechanik bekannte Gleichung für den Ort s = a t 2 . Wenn Sie beides
2
verbinden sollten Sie bereits die korrekte Formel für die Corioliskraft – in skalarer Schreibweise haben.
Bestimmen Sie nun auch die Corioliskraft für den Fall, dass sich der Ball in einem beliebigen Winkel von M
wegbewegt und zeigen Sie dass in vektorieller Schreibweise dafür die oben angegebene Formel richtig ist.
ω
M
v = r*t
Ausgabe am 10.11.2010, Besprechung in der Woche vom 15.-19.11.2010
x-Achse (Inertialsystem S)
Seite 2