5. Übung zur Theoretischen Physik in zwei Semestern I 23

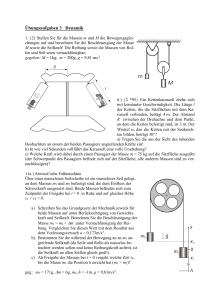
Prof. Dr. J. Krug
Dr. G. Wergen
Institut für Theoretische Physik
der Universität zu Köln - SS 2013
5. Übung zur Theoretischen Physik in zwei Semestern I
Abgabe: Dienstag 14. Mai bis 12 Uhr im Kasten vor dem Institut für Theoretische Physik
Diskussion: Freitag 17. Mai in den Übungen
Termine: Klausur am 1. August (Donnerstag) um 14:15 Uhr in HS I
Internetseite: http://www.thp.uni-koeln.de/∼gw/
23. Kometenbahn
(4+4 = 8 Punkte)
Ein Komet wird in einer Entfernung von 108 km von der Sonne beobachtet. Er hat eine Geschwindigkeit von 60 km/s in einer Richtung, die derartig einen Winkel von 30◦ mit der Verbindungslinie zur Sonne einschließt, daß er sich dieser nähert. Die Masse des Kometen beträgt
104 kg.
a) Berechnen Sie den Betrag des Drehimpulses, die kinetische Energie und Gesamtenergie
relativ zum Unendlichen des Kometen. Ist die Bahn eine Ellipse oder eine Hyperbel?
b) Bis auf welchen Abstand wird sich der Komet der Sonne nähern? Wie groß ist sein Geschwindigkeit im sonnennächsten Punkt?
24. Verallgemeinerte Potentiale, starke Wechselwirkung
(4+8 = 12 Punkte)
In dieser Aufgabe soll die Bewegung eines Teilchens der Masse m in einem fiktiven Gravitationspotential der Form
V (r) = −
αν
rν
mit ν < 2 und α > 0 untersucht werden. Für positive ν beschreibt dies ein Potential welches,
wie das wahre Gravitationspotential (ν = 1), im Ursprung nach −∞ strebt und im Unendlichen
verschwindet, während es für ν < 0 im Ursprung verschwindet und im Unendlichen gegen +∞
strebt; für ν = −2 ergibt sich z.B. der dreidimensionale harmonische Oszillator.
a) Wie lautet die Verallgemeinerung des dritten Keplerschen Gesetzes für die Kreisbahnen im
obigen Potential? Benutzen Sie die Balance von Gravitationskraft und Zentripetalkraft.
b) Wir betrachten nun den speziellen Fall des Potentiales V (r) = αr (für r > 0), welches in der
Beschreibung der starken Wechselwirkung von Bedeutung ist. Die lineare r-Abhängigkeit
des Potentiales führt in der starken Wechselwirkung zum sogenannten Confinement der
Quarks. Diskutieren Sie die (klassisch) möglichen Bahnen in einem derartigen Potential, woher stammt der Begriff Confinement? Betrachten Sie, wie in Aufgabe 21 (Blatt 4),
fast kreisförmige Bahnen in diesem Potential und bestimmen Sie die Umlauf- und Oszillationsfrequenz, sowie deren Verhältnis zueinander. Diskutieren Sie Ihr Ergebnis, gibt es
geschlossene Bahnen?
1
25. Dreikörperproblem nach Lagrange
(8 Punkte)
Im Allgemeinen ist keine exakte Lösung des Dreikörperproblems bekannt. In einigen Spezialfällen
ist es jedoch lösbar. 1772 untersuchte Lagrange den speziellen Fall von drei Körpern, die auf den
Ecken eines gleichseitigen Dreiecks (mit Seitenlänge a) angeordnet sind. Die Bewegung wird in der
Dreiecksebene und in Form einer Drehung um den Massenschwerpunkt ablaufen. Wir betrachten
den Fall von drei gleich großen Massen mit Masse m. Setzen Sie die Gravitationskraft, die auf
eine der drei Massen wirkt, mit der Zentripetalkraft, die sich aus der Kreisbewegung ergibt gleich
und bestimmen Sie somit die Rotationsgeschwindigkeit. Verallgemeinern Sie Ihr Resultat auf vier
gleichgroße Massen, die sich an den Ecken eines Quadrates befinden.
26. Atwood’sche Fallmaschine
(12 Punkte)
Wir betrachten eine masselose Rolle (mit Radius R), über die zwei Massen, m1 und m2 , miteinander verbunden sind (siehe Abbildung). Auf die Massen wirke das Schwerefeld der Erde. Stellen
Sie die Zwangsbedingung für die Koordinaten (x1 , x2 , y1 , y2 , z1 , z2 ) und die Lagrangegleichung 1.
~ 1 und Z
~2.
Art auf. Lösen Sie die Bewegungsgleichungen und bestimmen Sie die Zwangskräfte Z
Welche Bedeutung haben die trägen und schweren Massen der beiden Körper? Was passiert mit
~1 + Z
~ 2 , die die Rollenachse aufnehmen muss, wenn die beiden Massen annähernd
der Kraft Z
gleich sind, also m1 → m2 ?
~1 + Z
~2
Z
y
~g
~2
Z
m2
~1
Z
m2~g
m1
x
m1~g
2