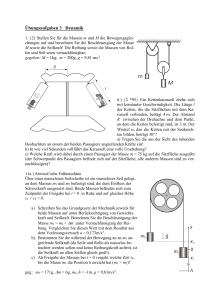
Angabe

Prüfungsablauf:
 PC einschalten, anmelden, MathCad starten
 Netzwerkstecker herausziehen
 Aufgaben lösen, Zwischenspeicherung auf lokaler Festplatte
Bei Abgabe am Ende der Arbeit:
 Ergebnisse zur Sicherheit auf 2 (!!) Disketten abspeichern, Disketten mit Namen
beschriften
 Netzwerkstecker wieder hineinstecken, Ergebnisse drucken
 PC herunterfahren
 Kontrolle, ob alle ausgedruckten Seiten mit Namen versehen sind. Nötigenfalls
handschriftlich ergänzen.
Weitere Hinweise:
 Unbedingt auf jeder Seite des MathCad-Dokuments den Namen angeben
 Erstellen Sie ein übersichtliches MathCad-Dokument, aus dem jeder Denk/Rechenschritt
klar hervorgeht. Beantworten Sie die Fragen mit vollständigen Sätzen.
 Handschriftliche Überlegungen zu den MathCad-Aufgaben sind ebenfalls abzugeben.
Jedes abgegebene Blatt mit dem Namen beschriften.
 Bei Grafiken ist auf eine sinnvolle Wahl der Achsenskalierungen zu achten. Diese wird
mit beurteilt !
 Die handschriftlich gelösten Aufgaben sind so zu dokumentieren, dass jeder
Rechenschritt nachvollziehbar ist.
 In MathCad: Einheitensystem ausschalten, Startindex auf 1 setzen
Abzugeben sind:
 Blätter mit den Aufgabenstellungen
 Disketten
 Ausdrucke
 Blätter mit Lösungen des handschriftlichen Teils
 eventuell verwendete Formelsammlung (mit Namen !)
Mathematik – Klausur
Verfahrens- und Umwelttechnik
24.11.2004
1. Aus einer Kugel vom Radius R=5 cm wird eine kegelförmige
Bohrung (Kegelspitze im Mittelpunkt der Kugel, Öffnungswinkel des
Kegels = 90°) gebohrt.
Berechnen Sie das Volumen des entstehenden Körpers mit Hilfe der
Integralrechnung.
2. Der zeitliche Verlauf einer chemischen Reaktion vom Typ
2AB
wird beschrieben durch die Differentialgleichung
dy A (t )
2
  k   y A (t )
dt
wobei yA(t) die Konzentration der Substanz A zum Zeitpunkt t angibt und k eine Konstante
darstellt.
a. Lösen Sie diese Differentialgleichung allgemein.
Die Konzentration der Substanz A fällt von 10 mg/l (bei t = 0) innerhalb von 3.5 Sekunden
auf 7 mg/l ab.
b. Bestimmen Sie aus diesen Angaben die Konstante k und die Integrationskonstante.
Falsches Zwischenergebnis: k = 0.015
c. Wie lange dauert es, bis die Konzentration von A auf 1 mg/l abgenommen hat ?
d. Simulieren Sie mit Excel den Verlauf von y(t) zwischen t=0 und t=5 Sekunden in Schritten
von t = 0.1 Sekunden. Stellen Sie den Verlauf von T(t) graphisch dar. (Hinweis zum
Ausdrucken: Plazieren Sie die Grafik an eine freie Stelle in den oberen Bereich des
Arbeitsplatzes und drucken Sie nur Seite 1 aus.)
Aufgabe d ist auch ohne a/b/c lösbar !
3. Gegeben ist folgendes System von gekoppelten Massen:
Massen: 20 Gramm;
Federkonstante der mittleren Feder: 3 N/m
Federkonstante der beiden anderen Federn: 1 N/m
a. Bestimmen Sie die Eigenfrequenzen des Systems in Hertz.
b. Bestimmen Sie die Form der Eigenschwingung mit der höchsten Frequenz und
beschreiben Sie diese verbal. Wie verhalten sich die Amplituden der einzelnen Massen
zueinander ?
4. Beantworten Sie folgende Fragen in Form eines Aufsatzes (in dem aber natürlich schon
mathematische Beziehungen vorkommen sollen):
a. Was versteht man unter den Eigenschwingungen eines schwingungsfähigen Systems ?
b. Was versteht man unter den Eigenwerten und Eigenvektoren einer Matrix ?
c. Warum lassen sich die Eigenfrequenzen eines ungedämpften, schwingungsfähigen Systems
aus den Eigenwerten einer Matrix berechnen ?
5. Gegeben ist die Differentialgleichung
y’’ + 6y’ + 9y = 2x
Bestimmen Sie
a. die Lösung der zugehörigen homogenen Differentialgleichung.
b. die allgemeine Lösung der inhomogenen Differentialgleichung.
1. 4 P.
2. 2+2+1+2 P.
3. 4+2 P.
4. je 2 P.
5. 2+3 P.