Mathematische Zeichen und Symbole

R. Brinkmann http://brinkmann-du.de
Seite 1
27.01.2009
Mathematische Zeichen und Symbole
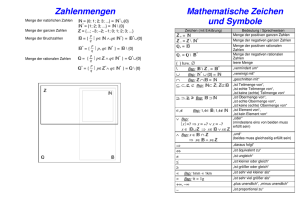
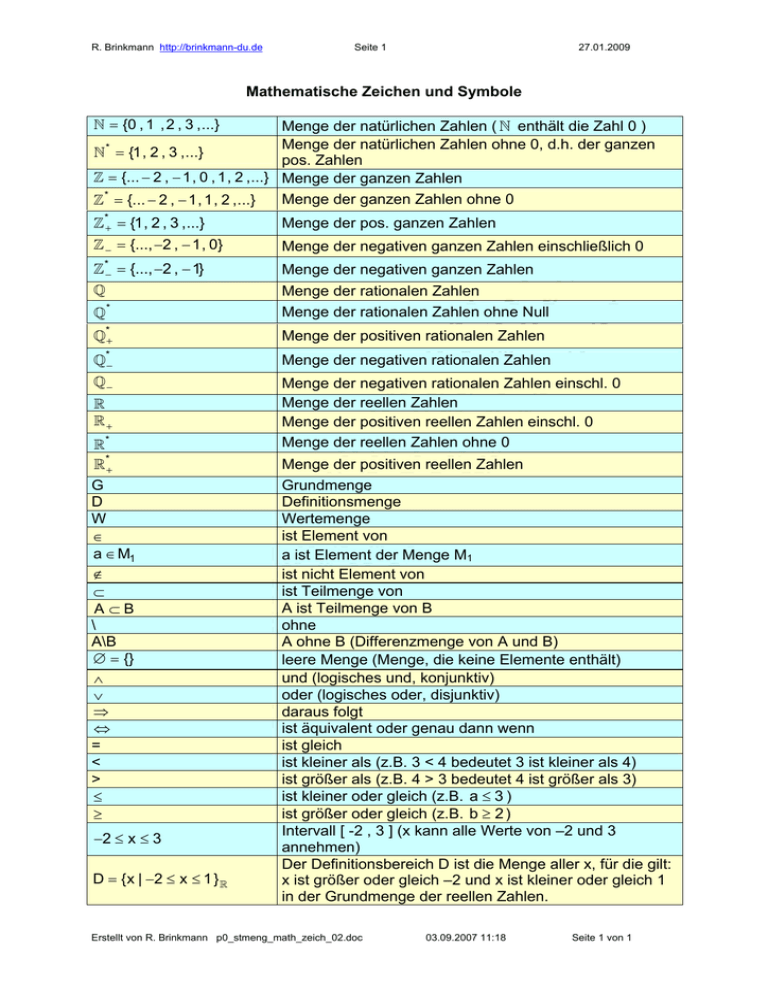
` = {0 , 1 ,2 , 3 ,...}
Menge der natürlichen Zahlen ( ` enthält die Zahl 0 )
Menge der natürlichen Zahlen ohne 0, d.h. der ganzen
` * = {1, 2 , 3 ,...}
pos. Zahlen
] = {... − 2 , − 1, 0 , 1, 2 ,...} Menge der ganzen Zahlen
Menge der ganzen Zahlen ohne 0
] * = {... − 2 , − 1, 1, 2 ,...}
]*+ = {1, 2 , 3 ,...}
Menge der pos. ganzen Zahlen
] − = {..., −2 , − 1, 0}
Menge der negativen ganzen Zahlen einschließlich 0
]*−
= {..., −2 , − 1}
_
_
*
Menge der negativen ganzen Zahlen
Menge der rationalen Zahlen
Menge der rationalen Zahlen ohne Null
_*+
Menge der positiven rationalen Zahlen
_*−
Menge der negativen rationalen Zahlen
_−
Menge der negativen rationalen Zahlen einschl. 0
Menge der reellen Zahlen
Menge der positiven reellen Zahlen einschl. 0
Menge der reellen Zahlen ohne 0
\
\+
\*
\*+
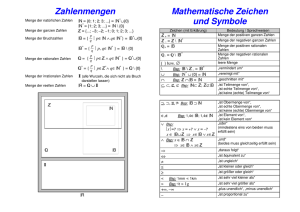
G
D
W
∈
a ∈ M1
∉
⊂
A ⊂B
\
A\B
∅ = {}
∧
∨
⇒
⇔
=
<
>
≤
≥
−2 ≤ x ≤ 3
D = {x | −2 ≤ x ≤ 1 } \
Menge der positiven reellen Zahlen
Grundmenge
Definitionsmenge
Wertemenge
ist Element von
a ist Element der Menge M1
ist nicht Element von
ist Teilmenge von
A ist Teilmenge von B
ohne
A ohne B (Differenzmenge von A und B)
leere Menge (Menge, die keine Elemente enthält)
und (logisches und, konjunktiv)
oder (logisches oder, disjunktiv)
daraus folgt
ist äquivalent oder genau dann wenn
ist gleich
ist kleiner als (z.B. 3 < 4 bedeutet 3 ist kleiner als 4)
ist größer als (z.B. 4 > 3 bedeutet 4 ist größer als 3)
ist kleiner oder gleich (z.B. a ≤ 3 )
ist größer oder gleich (z.B. b ≥ 2 )
Intervall [ -2 , 3 ] (x kann alle Werte von –2 und 3
annehmen)
Der Definitionsbereich D ist die Menge aller x, für die gilt:
x ist größer oder gleich –2 und x ist kleiner oder gleich 1
in der Grundmenge der reellen Zahlen.
Erstellt von R. Brinkmann p0_stmeng_math_zeich_02.doc
03.09.2007 11:18
Seite 1 von 1