Zahlenmengen Mathematische Zeichen und Symbole

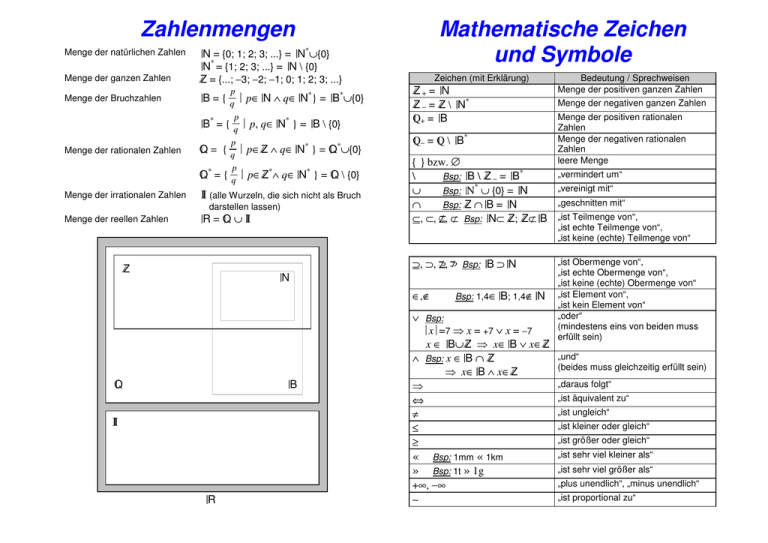
Zahlenmengen
Menge der natürlichen Zahlen
= {0; 1; 2; 3; ...} = N*∪{0}
N = {1; 2; 3; ...} = N \ {0}
/Z = {...; −3; −2; −1; 0; 1; 2; 3; ...}
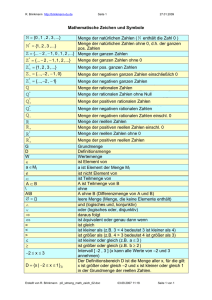
Mathematische Zeichen
und Symbole
N
*
Menge der ganzen Zahlen
Menge der Bruchzahlen
Menge der rationalen Zahlen
Menge der irrationalen Zahlen
p
*
*
B = {  p∈N ∧ q∈N } = B ∪{0}
q
p
*
*
B = {  p, q∈N } = B \ {0}
q
p

Q = { q  p∈/Z ∧ q∈N* } = Q*∪{0}
p

Q* = { q  p∈/Z*∧ q∈N* } = Q \ {0}
II (alle Wurzeln, die sich nicht als Bruch
darstellen lassen)
Menge der reellen Zahlen
R
= Q ∪ II
Zeichen (mit Erklärung)
/Z + = N
*
/Z − = /Z \ N

Q+
= B

Q−
= Q \ B*
= B*
*
Bsp: N ∪ {0} = N
Bsp: /Z ∩B = N
, ⊄ Bsp: N⊂ /Z; /Z⊄B
Bsp: B \ /Z −
⊇, ⊃, ,
/Z
Menge der positiven rationalen
Zahlen
Menge der negativen rationalen
Zahlen
leere Menge
{ } bzw. ∅
\
∪
∩
⊆, ⊂,
Bsp: B
⊃N
N
∈,∉

Q
B
II
R
Bedeutung / Sprechweisen
Menge der positiven ganzen Zahlen
Menge der negativen ganzen Zahlen
Bsp: 1,4∈B; 1,4∉N
∨ Bsp:
x=7 ⇒ x = +7 ∨ x = −7
x ∈ B∪/Z ⇒ x∈B ∨ x∈/Z
∧ Bsp: x ∈B ∩ /Z
⇒ x∈B ∧ x∈/Z
⇒
⇔
≠
≤
≥
« Bsp: 1mm « 1km
» Bsp: 1t » 1g
+∞, −∞
∼
„vermindert um“
„vereinigt mit“
„geschnitten mit“
„ist Teilmenge von“,
„ist echte Teilmenge von“,
„ist keine (echte) Teilmenge von“
„ist Obermenge von“,
„ist echte Obermenge von“,
„ist keine (echte) Obermenge von“
„ist Element von“,
„ist kein Element von“
„oder“
(mindestens eins von beiden muss
erfüllt sein)
„und“
(beides muss gleichzeitig erfüllt sein)
„daraus folgt“
„ist äquivalent zu“
„ist ungleich“
„ist kleiner oder gleich“
„ist größer oder gleich“
„ist sehr viel kleiner als“
„ist sehr viel größer als“
„plus unendlich“, „minus unendlich“
„ist proportional zu“