Was stimmt jetzt - Antonkriegergasse

Was stimmt jetzt: Erlaubt oder nicht erlaubt?
C4a
Warum soll plötzlich erlaubt sein, was uns Lehrer und LehrerInnen jahrelang verboten haben? Bisher gab’s
für Unsinn wie ! 9 = !3 bei Schularbeiten ja immerhin Punkteabzüge, mit der Begründung: Wurzeln
aus negativen Zahlen gibt es nicht, weil jedes Quadrat positiv ist, auch (-3).(-3) = +9. Wenn man jetzt neue
Zahlen (die imaginären) erfindet mit 3i.3i = 9i² = 9.(-1) = -9, na da könnte ja jeder kommen und neue
Zahlen erfinden. Gewiefte SchülerInnen könnten bei unlösbaren Gleichungen z.B. eine neue Zahl z
erfinden und sie kurzerhand zur Lösung des sonst unlösbaren Beispieles erklären, oder nicht?
Nun gut so einfach ist die Sache leider (oder zum Glück?) nun auch wieder nicht. Gleichungen spiegeln ja
im Normalfall ein reales Problem wieder, und die Lösung sollte nicht nur eine willkürlich erfundene Zahl
sein, sondern auch das wirkliche Problem lösen. Ein Unternehmer, der den besten Verkaufspreis zur
Ermittlung des höchsten Gewinnes sucht, wird mit dem Ergebnis 5z/2 nichts anfangen, weil die willkürliche
Zahl z ihm nicht sagt, wie hoch er den Verkaufspreis ansetzten soll.
Zum Glück ist es bei den imaginären Zahlen anders: Es hat sich gezeigt, dass diese Zahlen in Verbindung
mit den bereits gezeigten Rechengesetzten durchaus sinnvoll interpretierbare Lösungen liefern, oft sind
auch nur Zwischenergebnisse „imaginär“, während die Endergebnisse „schöne“ und klare Ergebnisse sind,
also im Allgemeinen „reelle“ Zahlen.
Problem bleibt aber, dass man sich die imaginäre Zahlen (imaginär = „nur in der Vorstellung existierend“)
eigentlich überhaupt nicht gut oder eigentlich gar nicht vorstellen kann. Dazu kommt noch, dass
LehrerInnen jahrelang verboten haben, aus negativen Zahlen Wurzeln zu ziehen, das hinterlässt Spuren
und kann oft nur mit Unbehagen jetzt durchgeführt werden.
Diese Situation ist aber nicht neu: In der Volksschule lernt man, dass man immer die kleinere Zahl von der
größeren Abziehen muss: 5 - 3 = 2, aber 3 - 5 „geht nicht“, hat also keine Lösung. Ist ja auch klar, wer drei
Schilling hat, kann ja nicht fünf hergeben oder zahlen. Wenn man aber neue Zahlen erfindet, die „negativen
Zahlen“, sieht man sehr schnell, dass hier offensichtlich sinnvolle Ergebnisse und Interpretationen möglich
sind. -2 bedeutet dann halt 2 Schilling Schulden, oder das Sinken der Temperatur um 2 Grad oder
ähnliches. Die natürlichen Zahlen werden daher um die negativen Zahlen erweitert und ergeben mit
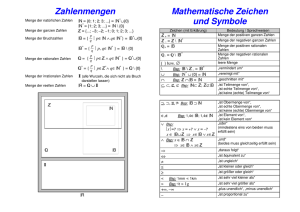
diesen zusammen die ganzen Zahlen:
Zahlbereichserweiterung von N = {1, 2, 3, 4, 5, ...} auf Z = { ...-3, -2, -1, 0, 1, 2, 3, ...}.
Ähnliches passiert später mit den Divisionen und Brüchen: 5 : 3 wird in der Volksschule eher mit „geht
nicht“ oder höchsten als Division mit Rest angesehen, immerhin ist die Lösung ja in den ganzen Zahlen
nicht zu finden. Definiert man aber die Menge Q der rationalen Zahlen hat man plötzlich die Lösung des
Problems: 5/3 oder in Dezimalschreibweise: 1,6666.... Q ist bekanntlich die Menge aller als Bruch
darstellbaren Zahlen.
Zahlbereichserweiterung von Z = { ...-3, -2, -1, 0, 1, 2, 3, ...} auf Q = {a/b)/ a,b ∈ Z; b ≠ 0}
Die Entwicklung des Zahlbegriffes bei Kindern und SchülerInnen heute hat ihre Entsprechung bei der
historischen Entwicklung des Zahlbegriffes vom Altertum bis jetzt. Für die Pythagoräer (ca. 500 v. Chr.,
Schüler und Anhänger von Pythagoras) war jedenfalls mit den Rationalen Zahlen der Schlusspunkt
erreicht: Zahlen, die nicht als Bruch (damals Verhältnis) darstellbar waren, wurden kurzerhand als nicht
existent erklärt, sofern überhaupt jemand auf die Idee kam an so etwas „ketzerisches“ zu denken.
Allerdings bekamen sie bei der Lösung recht einfacher Sachen erhebliche Probleme: Wie lang ist die
Diagonale eines Quadrates mit Seitenlänge eins? Für die Pythagoräer ergab die einfache Rechnung:
Diejenige Zahl, die quadriert zwei ergibt: x² = 2. Das Problem war nur, dass man keinen Bruch aus der
Menge Q finden konnte, der quadriert zwei ergibt! Es konnte später gezeigt werden, dass es so einen
Bruch nicht gibt! Man mußte um eine Lösung des Problems zu erhalten, den Zahlbereich wieder erweitern.
Offensichtlich gibt es ja eine Diagonale des Quadrates und niemand wird abstreiten, dass diese auch eine
bestimmte Länge hat. Um auch solche Probleme lösen zu können mußte man die irrationalen Zahlen I
wie z.B. 2 = 1,41421.... , oder ! = 3,14... , e= 2,71.... (Euler’sche Zahl) u.s.w. zu den rationalen
Zahlen Q hinzunehmen. ( Irrational waren alle Zahlen mit unendlich vielen Dezimalstellen, die sich aber
nicht wiederholen, also nichtperiodisch sind). Zusammen mit den rationalen Zahlen hat man nun den
Zahlbereich der reellen Zahlen erreicht, die alle uns bisher bekannten Zahlen umfasst.
Zahlbereichserweiterung von Q auf R = Q ! I : die reellen Zahlen sind alle rationalen Zahlen (Brüche)
und alle irrationalen Zahlen (unendlich nicht periodische Dezimalzahlen) zusammen.