Reell : rational – irrational Irrationalität von π
Werbung

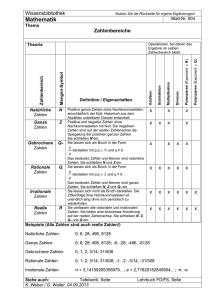
13 Reell : rational – irrational D213-01 mathbuch 3 LU 13 Begleitband+ Zusatzmaterial Irrationalität von π Die irrationalen Zahlen – daher wohl auch der Name «irrational» – lassen sich tatsächlich schwerer fassen als die rationalen. Es sind Dezimalzahlen, die unendlich viele Stellen nach dem Komma aufweisen, ohne wiederkehrende Ziffernfolge. Sie lassen sich nicht als Bruch darstellen. 8.5 pt z ist irrational a z ≠ __ b mit a, b ,b≠0 7.5 pt Auf der Sekundarstufe I erhält man vor allem durch das Ziehen der Quadratwurzel von rationalen Zahlen Ergebnisse mit irrationalen Zahlen, später können auch die Ergebnisse von Logarithmen, trigonometrischen Berechnungen oder Potenzen irrational sein. Den Lernenden ist die irrationale Zahl π bereits bekannt. Dies macht deutlich, dass irrationale Zahlen bei geometrischen Berechnungen eine zentrale Rolle spielen. Dennoch sollte das Rechnen mit reellen bzw. irrationalen Zahlen den Lernenden nicht allzu schwerfallen: Sie finden, wie die rationalen Zahlen auch, auf dem Zahlenstrahl Platz, der Abstand von einigen irrationalen Zahlen zu 0 lässt sich sogar konstruieren. Es gelten alle bisher bekannten Rechengesetze. Sämtliche bekannten Operationen mit reellen Zahlen führen wieder zu reellen Zahlen. Es gibt auch Ausnahmen, z. B. Quadratwurzel aus einer negativen Zahl. Beweis __ Unten stehend ein Beweis, dass √ 2 irrational ist. Interessierte Lernende sind durchaus in der Lage, einer Moderation dieses Beweises zu folgen. __ Behauptung: √ 2 ist nicht durch einen Bruch darstellbar. __ Wir beweisen dies «indirekt»: Wir nehmen zuerst einmal an, √ 2 sei ein Bruch. Aus dieser Annahme ziehen wir einige Schlussfolgerungen, die auf einen Widerspruch zum Ausgangspunkt (eben die Annahme, __ √ 2 sei ein gewöhnlicher Bruch) führen. Annahme __ p √ 2 = __ sei ein gekürzter Bruch. q Sein Wert liegt zwischen 1,4 und 1,5, ist also sicher keine ganze Zahl. Widerspruch p Damit kann __ kein gekürzter Bruch sein. q www.mathbuch.info 2 p Dann gilt: 2 = __ 2 und auch p 2 = 2q 2 q Dann ist aber p 2 eine gerade Zahl, und somit muss auch p eine gerade Zahl sein, damit ist p 2 sogar eine 4er-Zahl, und dann muss auch 2 · q 2 eine 4er-Zahl sein und demzufolge q 2 gerade, also ist auch q gerade. Dies heisst nun aber, dass p und q beide gerade sind, also den gemeinsamen Teiler 2 haben. Als Kopiervorlage freigegeben © Schulverlag plus AG / Klett und Balmer Verlag AG, 2015 1 | 1