ma_004 | Zahlenbereiche - walter-schule.de

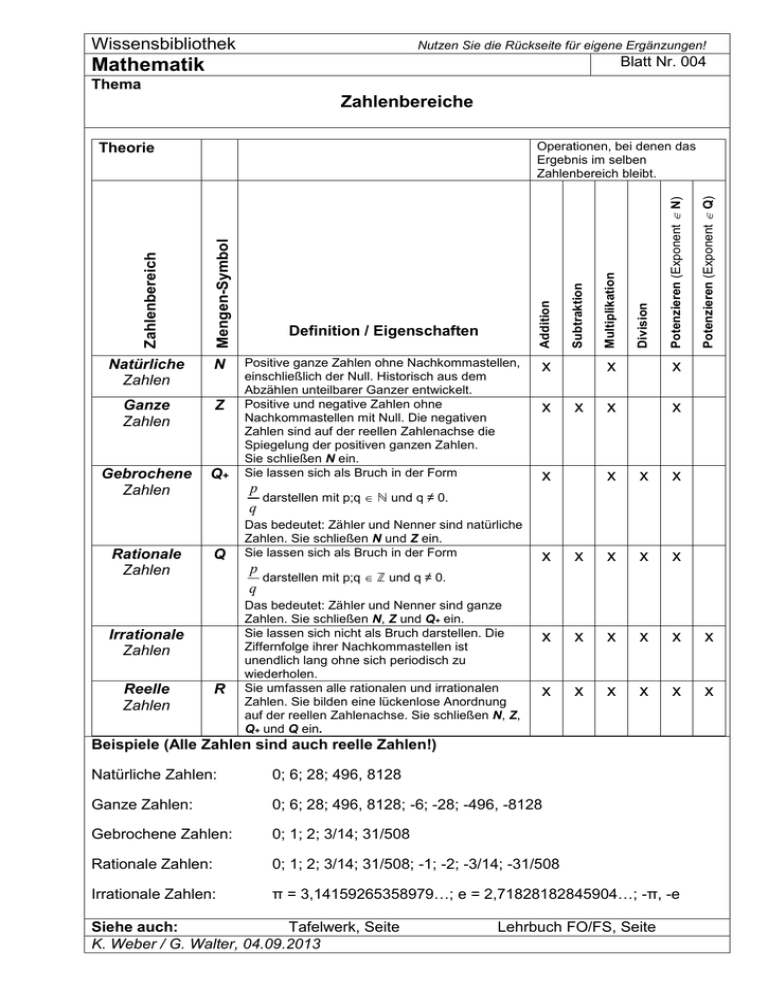
Wissensbibliothek
Nutzen Sie die Rückseite für eigene Ergänzungen!
Blatt Nr. 004
Mathematik
Thema
Zahlenbereiche
N
Ganze
Zahlen
Z
Gebrochene
Zahlen
Q+
Rationale
Zahlen
Positive ganze Zahlen ohne Nachkommastellen,
einschließlich der Null. Historisch aus dem
Abzählen unteilbarer Ganzer entwickelt.
Positive und negative Zahlen ohne
Nachkommastellen mit Null. Die negativen
Zahlen sind auf der reellen Zahlenachse die
Spiegelung der positiven ganzen Zahlen.
Sie schließen N ein.
Sie lassen sich als Bruch in der Form
p
darstellen mit p;q  ℕ und q ≠ 0.
q
Q
Das bedeutet: Zähler und Nenner sind natürliche
Zahlen. Sie schließen N und Z ein.
Sie lassen sich als Bruch in der Form
p
darstellen mit p;q  ℤ und q ≠ 0.
q
Irrationale
Zahlen
Reelle
Zahlen
R
Das bedeutet: Zähler und Nenner sind ganze
Zahlen. Sie schließen N, Z und Q+ ein.
Sie lassen sich nicht als Bruch darstellen. Die
Ziffernfolge ihrer Nachkommastellen ist
unendlich lang ohne sich periodisch zu
wiederholen.
Sie umfassen alle rationalen und irrationalen
Zahlen. Sie bilden eine lückenlose Anordnung
auf der reellen Zahlenachse. Sie schließen N, Z,
Q+ und Q ein.
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Beispiele (Alle Zahlen sind auch reelle Zahlen!)
Natürliche Zahlen:
0; 6; 28; 496, 8128
Ganze Zahlen:
0; 6; 28; 496, 8128; -6; -28; -496, -8128
Gebrochene Zahlen:
0; 1; 2; 3/14; 31/508
Rationale Zahlen:
0; 1; 2; 3/14; 31/508; -1; -2; -3/14; -31/508
Irrationale Zahlen:
π = 3,14159265358979…; e = 2,71828182845904…; -π, -e
Siehe auch:
Tafelwerk, Seite
K. Weber / G. Walter, 04.09.2013
Potenzieren (Exponent  Q)
Potenzieren (Exponent  N)
Division
Multiplikation
Addition
Mengen-Symbol
Zahlenbereich
Natürliche
Zahlen
Definition / Eigenschaften
Subtraktion
Operationen, bei denen das
Ergebnis im selben
Zahlenbereich bleibt.
Theorie
Lehrbuch FO/FS, Seite